Файл: Г.М. Гринфельд лекции по курсу дискретные системы автоматического управления.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.07.2024
Просмотров: 307
Скачиваний: 0
СОДЕРЖАНИЕ
1.1 Типы квантования непрерывных сигналов.
1.2. Решетчатые функции разностные уравнения.
1.3. Обобщенная структурная схема дискретной системы.
1.4. Простейший импульсный элемент. Формирующий элемент. Фиксатор.
2. Основы теории z-преобразования
2.1. Дискретное преобразование Лапласа. Z-преобразование.
2.2. Основные теоремы z-преобразования.
2.3. Передаточная функция разомкнутой дискретной системы.
2.4. Последовательное соединение звеньев в дискретных сау.
2.5. Передаточная функция замкнутой дискретной системы.
2.6. Обратное z-преобразование.
3. Анализ устойчивости и точности
3.1 Прямой метод оценки устойчивости.
3.2 Критерий устойчивости Шур-Кона.
3.3 Критерий устойчивости, использующий билинейное преобразование.
3.4. Абсолютно устойчивые системы.
3.5. Анализ точности дискретных систем.
4. Частотные характеристики дискретных систем
4.1. Теорема Котельникова-Шеннона.
4.2. Логарифмические частотные характеристики дискретных сау.
5. Определение реакции дискретной сау
5.1. Метод дробного квантования.
5.2. Метод модифицированного z-преобразования.
6. Системы автоматического управления
6.2. Передаточные функции цву, реализующего типовые законы управления.
7. Коррекция цифровых систем управления
7.1. Коррекция дискретных сау с помощью непрерывных регуляторов.
7.2. Коррекция сау с помощью цифровых регуляторов.
7.3. Физическая реализуемость цифровых регуляторов.
7.4. Реализация цифровых регуляторов импульсными фильтрами.
7.5. Реализация цифровых регуляторов на базе цву.
8. Методические указания и вариаты расчетно-графического задания
Если на выходе квантователя установлен идеальный фильтр низких частот, обладающей частотной характеристикой:
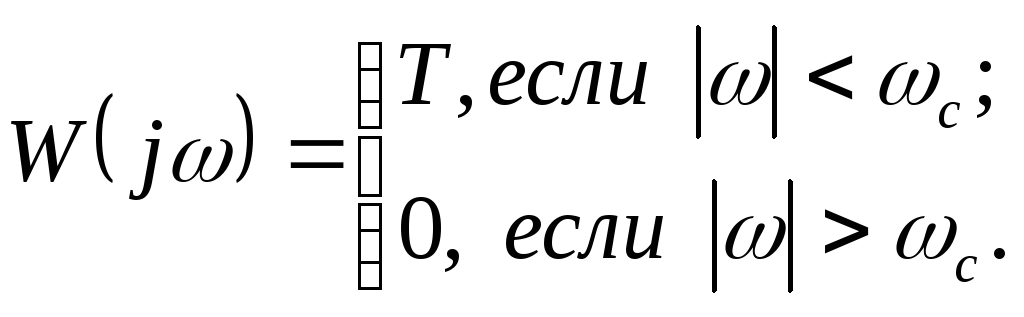 (36)
(36)

Рис.28. Финитный спектр входного сигнала

Рис.29.
Спектр выходного сигнала
![]()

Рис.30.
Спектр выходного сигнала
![]()
то спектр его
выходного сигнала во всем частотном
диапазоне будет совпадать со спектром
квантуемого сигнала, т.е. на выходе
такого фильтра будет восстановлен
сигнал
![]() .
.
Следовательно, если непрерывный сигнал
![]() обладает финитным спектром с частотой
среза
обладает финитным спектром с частотой
среза![]() ,
то квантование по времени этого сигнала
с частотой
,
то квантование по времени этого сигнала
с частотой![]() не приводит к его искажению (теорема
Котельникова-Шеннона).
не приводит к его искажению (теорема
Котельникова-Шеннона).
Необходимо отметить следующие ограничения, связанные с применением сформулированной теоремы: во-первых, частотная характеристика формирующего элемента, подключенного к выходу квантователя, существенно отличается от (36)) (в частности, для фиксатора в этом легко убедиться, сопоставив (8) и (36): во-вторых, не существует реальных сигналов с финитным спектром, хотя их высокочастотные составляющие могут быть сильно ослабленными.
4.2. Логарифмические частотные характеристики дискретных сау.
Логарифмические амплитудно- и фазо-частотные характеристики (ЛАХ и АФХ) широко используются при анализе и синтезе непрерывных САУ. Но для дискретных систем непосредственно использование обычных методов построения этих характеристик невозможно. Причина в том, что передаточные функции непрерывных САУ, по которым осуществляется построение характеристик, являются дробно-рациональными функциями комплексной переменной pи могут быть выражены в виде линейных или квадратичных множителей, а передаточные функции дискретных систем являются трансцендентными функциями оператораp.
Z-преобразование
превращает трансцендентную передаточную
функцию от pв
рациональную отz. Но
для построения ЛАХ и АФХ необходимо
также, чтобы с изменением частоты![]() комплексная переменная, являющаяся
аргументом передаточной функции,
изменялась вдоль мнимой оси комплексной
плоскости (например
комплексная переменная, являющаяся
аргументом передаточной функции,
изменялась вдоль мнимой оси комплексной
плоскости (например![]() ).
Но поскольку зависимость между
комплексными переменнымиzиpопределяются
формулой (13), и, следовательно:
).
Но поскольку зависимость между
комплексными переменнымиzиpопределяются
формулой (13), и, следовательно:
![]()
то при изменении частоты комплексная переменная zперемещается по единичной окружности вокруг начала координат комплексной плоскостиZ.
Поэтому необходимо введение такого преобразования, которое отражало бы единичную окружность на плоскости Zв мнимую ось другой комплексной плоскости. Такое отображение осуществляется с помощью билинейного преобразования (32), в соответствии с которым внутренняя часть единичного круга наz-плоскости отображается в левую полуплоскостьw, а внешняя часть этого круга – в правую полуплоскость.
Зависимость
между w и![]() :
:
![]()
Следовательно,
при изменении частоты
![]() комплексная переменнаяwперемещается вдоль мнимой оси.
комплексная переменнаяwперемещается вдоль мнимой оси.
![]()
Введем в
рассмотрение относительную псевдочастоту
![]() ,
равную:
,
равную:
![]()
На
основании (37) и (38) может быть получена
зависимость между
![]() и комплексной переменнойw:
и комплексной переменнойw:
![]()
которая
аналогична зависимости
![]() .
Разница лишь в том, что
.
Разница лишь в том, что![]() ,
в отличие от
,
в отличие от![]() ,
является безразмерной величиной. Поэтому
при построении ЛАХ и ФЧХ дискретных
систем будем использовать абсолютную
псевдочастоту,
имеющую как и
,
является безразмерной величиной. Поэтому
при построении ЛАХ и ФЧХ дискретных
систем будем использовать абсолютную
псевдочастоту,
имеющую как и![]() ,
размерность
,
размерность![]() .
.
Зависимость между абсолютной псевдочастотой и переменной w:
![]()
Таким
образом, построение ЛАХ дискретной САУ
осуществляется в следующей
последовательности: по передаточной
функции системы
![]() на основании (32) вычисляется передаточная
функция
на основании (32) вычисляется передаточная
функция![]() ,
по которой, используя (40), определяется
частотная характеристика
,
по которой, используя (40), определяется
частотная характеристика![]() .
Построение асимптотической ЛАХ по виду
.
Построение асимптотической ЛАХ по виду![]() производится по тем же правилам, что и
для непрерывных систем. При построении
ФЧХ следует обращать внимание на наличие
неминимально-фазового сомножителя
производится по тем же правилам, что и
для непрерывных систем. При построении
ФЧХ следует обращать внимание на наличие
неминимально-фазового сомножителя![]() в числителе функции
в числителе функции![]() .
Определяемая им составляющая в ФЧХ
равна:
.
Определяемая им составляющая в ФЧХ
равна:![]() .
.
В диапазоне
частот, где
![]() и, следовательно,
и, следовательно,![]() ,
построение ЛАХ и АФХ дискретных систем
можно производить непосредственно
функции ПНЧ
,
построение ЛАХ и АФХ дискретных систем
можно производить непосредственно
функции ПНЧ![]() .
Это значительно упрощает анализ точности
дискретных САУ, осуществляемый по виду
низкочастотного участка ЛАХ.
.
Это значительно упрощает анализ точности
дискретных САУ, осуществляемый по виду
низкочастотного участка ЛАХ.
Пример 23. Необходимо построить ЛАХ и ФЧХ дискретной САУ, передаточная функция которой:
![]() .
.
Преобразованная передаточная функция:
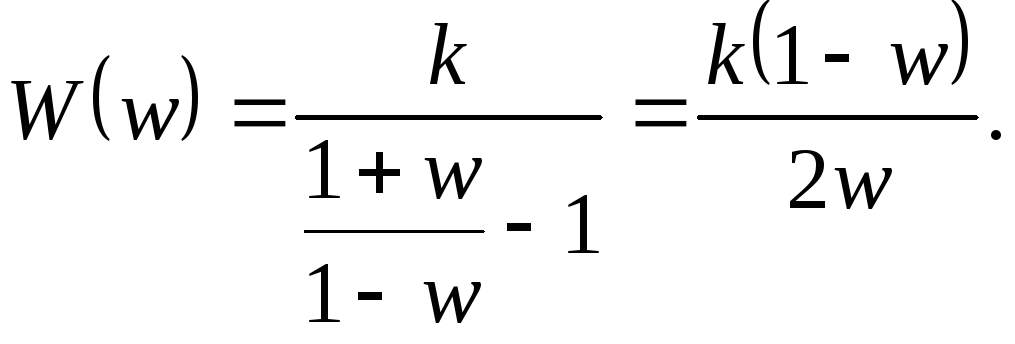
Частотная характеристика:
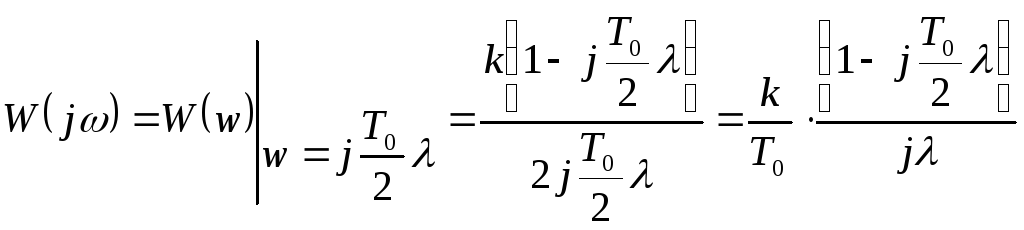 .
.
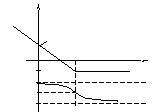
Рис.31. Графики ЛАХ и ФЧХ к примеру 23
Логарифмическая амплитудно-частотная характеристика:
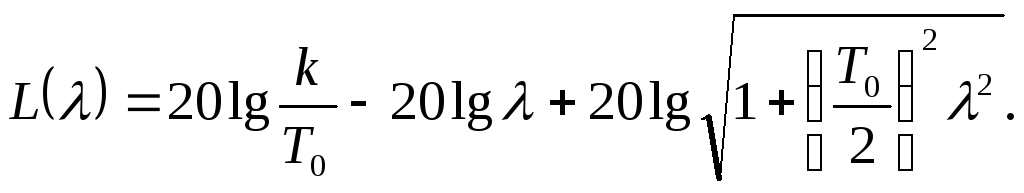
Фазо-частотная характеристика:
![]()
Графики ЛАХ и ФЧХ приведены на рис. 31.
5. Определение реакции дискретной сау
МЕЖДУ МОМЕНТАМИ КВАНТОВАНИЯ
Как уже
отмечалось, Z-преобразование
выходного сигнала дискретной системы
определяет значение функции![]() ,
только в моменты квантования
,
только в моменты квантования![]()
![]() .
Следовательно, методZ-преобразования
обладает достаточной точностью
применительно к тем системам, в которых
сигналы между двумя последовательными
моментами квантования изменяются не
существенно. Если же возникает
необходимость в определении реакции
системы между этими моментами, следует
использовать специальные методы,
например метод дробного квантования
или метод модифицированногоZ-преобразования.
.
Следовательно, методZ-преобразования
обладает достаточной точностью
применительно к тем системам, в которых
сигналы между двумя последовательными
моментами квантования изменяются не
существенно. Если же возникает
необходимость в определении реакции
системы между этими моментами, следует
использовать специальные методы,
например метод дробного квантования
или метод модифицированногоZ-преобразования.
5.1. Метод дробного квантования.
Как и
обычный метод Z-преобразования,
рассматриваемый метод не позволяет
найти непрерывный сигнал![]() ,
а лишь определить соответствующую ему
решетчатую функцию. Но дискреты этой
функции разделены интервалами времени,
равными
,
а лишь определить соответствующую ему
решетчатую функцию. Но дискреты этой
функции разделены интервалами времени,
равными![]() (гдеN– целое число),
т.е. расположены вNраз чаще по сравнению с дискретной
функцией
(гдеN– целое число),
т.е. расположены вNраз чаще по сравнению с дискретной
функцией![]() .
Обозначим такую решетчатую функцию
.
Обозначим такую решетчатую функцию![]() ,
а соответствующее ейZ-изображение
-
,
а соответствующее ейZ-изображение
-![]() .
Согласно методу дробного квантования
указанноеZ-изображение
равно
.
Согласно методу дробного квантования
указанноеZ-изображение
равно
![]() (41)
(41)
где
![]() может быть получена из обычной передаточной
функции системы
может быть получена из обычной передаточной
функции системы![]() заменой
в последнейzна
заменой
в последнейzна![]() ,
и
,
и![]() на
на![]() .
ВеличинаNопределяется
числом требуемых дополнительных значений
.
ВеличинаNопределяется
числом требуемых дополнительных значений![]() .
Если внутри интервала квантования
требуетсяRдополнительных
точек, то
.
Если внутри интервала квантования
требуетсяRдополнительных
точек, то![]() .
.