Файл: Г.М. Гринфельд лекции по курсу дискретные системы автоматического управления.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.07.2024
Просмотров: 313
Скачиваний: 0
СОДЕРЖАНИЕ
1.1 Типы квантования непрерывных сигналов.
1.2. Решетчатые функции разностные уравнения.
1.3. Обобщенная структурная схема дискретной системы.
1.4. Простейший импульсный элемент. Формирующий элемент. Фиксатор.
2. Основы теории z-преобразования
2.1. Дискретное преобразование Лапласа. Z-преобразование.
2.2. Основные теоремы z-преобразования.
2.3. Передаточная функция разомкнутой дискретной системы.
2.4. Последовательное соединение звеньев в дискретных сау.
2.5. Передаточная функция замкнутой дискретной системы.
2.6. Обратное z-преобразование.
3. Анализ устойчивости и точности
3.1 Прямой метод оценки устойчивости.
3.2 Критерий устойчивости Шур-Кона.
3.3 Критерий устойчивости, использующий билинейное преобразование.
3.4. Абсолютно устойчивые системы.
3.5. Анализ точности дискретных систем.
4. Частотные характеристики дискретных систем
4.1. Теорема Котельникова-Шеннона.
4.2. Логарифмические частотные характеристики дискретных сау.
5. Определение реакции дискретной сау
5.1. Метод дробного квантования.
5.2. Метод модифицированного z-преобразования.
6. Системы автоматического управления
6.2. Передаточные функции цву, реализующего типовые законы управления.
7. Коррекция цифровых систем управления
7.1. Коррекция дискретных сау с помощью непрерывных регуляторов.
7.2. Коррекция сау с помощью цифровых регуляторов.
7.3. Физическая реализуемость цифровых регуляторов.
7.4. Реализация цифровых регуляторов импульсными фильтрами.
7.5. Реализация цифровых регуляторов на базе цву.
8. Методические указания и вариаты расчетно-графического задания
Передаточная функция последовательного аналогового корректирующего звена равна:
![]() .
(67)
.
(67)
Полученная передаточная функция
![]() должна быть физически реализуемой. Для
этого количество полюсов
должна быть физически реализуемой. Для
этого количество полюсов![]() должно быть не меньше числа нулей. Полюса
функции
должно быть не меньше числа нулей. Полюса
функции![]() должны находиться в левой половине
должны находиться в левой половине![]() -
плоскости. Если необходимо, чтобы
корректирующее звено реализовывалось
с помощью
-
плоскости. Если необходимо, чтобы
корректирующее звено реализовывалось
с помощью![]() -
схем, передаточная функция
-
схем, передаточная функция![]() не должна иметь кратных полюсов.
не должна иметь кратных полюсов.
Для рассматриваемой системы:
![]()
По таблице
![]() -
преобразований находим:
-
преобразований находим:
![]()
Согласно (6) передаточная функция корректирующего звена:
![]() (68)
(68)
Для обеспечения физической реализуемости
![]() необходимо ввести в передаточную функцию
(68) дополнительный
достаточно удаленный полюс, существенно
не снижающий эффективности коррекции.
необходимо ввести в передаточную функцию
(68) дополнительный
достаточно удаленный полюс, существенно
не снижающий эффективности коррекции.
Окончательно полагаем
![]() (69)
(69)
Корректирующее звено с такой передаточной функцией может быть реализовано на одном операционном усилителе по схеме, приведенной на рис. 59. Расчет элементов схемы осуществляется исходя из следующих соотношений:
![]()
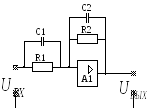
Рис. 59Реализация последовательного аналогового
корректирующего звена
Рассмотренный способ последовательного включения корректирующего звена не является единственно возможным. На рис. 60 приведена структурная схема дискретной САУ, коррекция которой осуществляется аналоговым регулятором, включенным в цепь обратной связи.
В этом случае передаточные функции разомкнутой скорректированной системы и корректирующего звена равны:
![]()
где выражение
![]() определено по формуле (66).
определено по формуле (66).
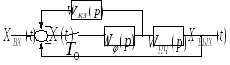
Рис. 60 Структурная схема дискретной САУ с аналоговым
корректирующим звеном в цепи обратной связи
Возможны и такие дискретные САУ, для коррекции которых аналоговые регуляторы включаются как в прямую, так и в цепь обратной связи.
На рис. 61 приведена структурная схема системы, коррекция которой осуществляется последовательным дискретным регулятором.
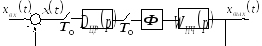
Рис. 61 Структурная схема дискретной САУ с последовательным
дискретным регулятором
Передаточная функция разомкнутой скорректированной системы равна:
![]()
Логарифмические амплитудно- и фазочастотные характеристики такой системы:
![]()
Если на основании требований к качеству
регулирования определен вид
![]() ,
можно построить ЛАХ корректирующего
звена:
,
можно построить ЛАХ корректирующего
звена:
![]() (70)
(70)
Дальнейшая последовательность действий
аналогична рассмотренной в предыдущем
пункте 6: по виду
![]() определяем выражение
определяем выражение![]() ;
далее, полагая
;
далее, полагая![]() ,
производим переход к
,
производим переход к![]() ;
затем, используя подстановку
;
затем, используя подстановку![]() ,
можно записать передаточную функцию
,
можно записать передаточную функцию![]() .
.
Полученная передаточная функция должна
быть физически реализуемой. Для этого
порядок знаменателя
![]() должен быть больше порядка числителя
или равен ему.
должен быть больше порядка числителя
или равен ему.
При построении
![]() для данного способа коррекции, учитывая
все требования к качеству регулирования,
необходимо также стремиться получить
достаточно простой вид ЛАХ корректирующего
звена. Это обеспечит приемлемую сложность
при его реализации.
для данного способа коррекции, учитывая
все требования к качеству регулирования,
необходимо также стремиться получить
достаточно простой вид ЛАХ корректирующего
звена. Это обеспечит приемлемую сложность
при его реализации.
Синтез дискетного корректирующего звена для рассматриваемой САУ осуществляется с учетом более жестких требований к точности по сравнению с рассмотренным вариантом непрерывной коррекции. Необходимо обеспечить нулевое значение установившейся ошибки по положению и добротность по скорости не менее пяти. С учетом этих, а также остальных требований к качеству регулирования, перечисленных в «Задании», построены логарифмические амплитудно-частотные характеристики скорректированной системы (рис.62).
90
20
0
0
-90
-20
-180
-40
-270
-60 400 20 2 1



















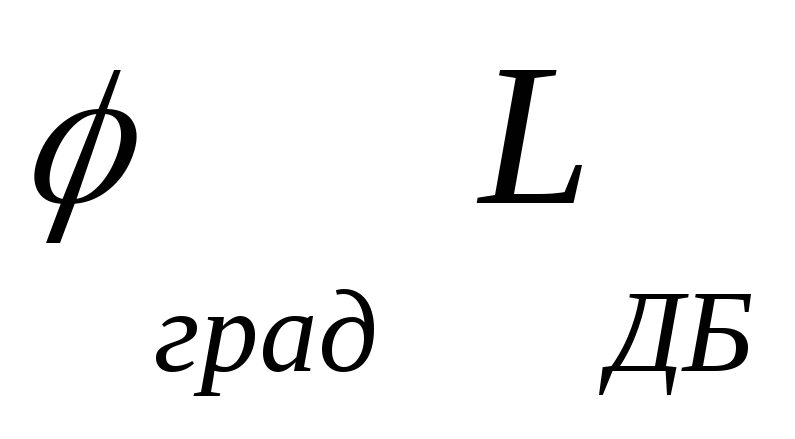

![]()








![]()
![]()
![]()

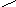
![]()
Рис. 62Логарифмические частотные характеристики САУ
с дискретным регулятором
Амплитудно-фазовая характеристика скорректированной системы полагается равной:
![]()
На рис.62 приведены также ЛАХ нескорректированной системы и корректирующего звена. Построение последней осуществлялось по формуле (70).
Амплитудно-фазовая характеристика корректирующего звена описывается выражением:
![]()
При этом передаточная функция регулятора,
записанная с использованием переменной
![]() ,
равна:
,
равна:
![]()
Искомая передаточная функция регулятора описывается выражением:
![]() (71)
(71)
Использование цифрового вычислительного устройства (ЦВУ) в качестве регулятора предполагает разработку соответствующей программы ЦВУ, отчего методы реализации передаточной функции
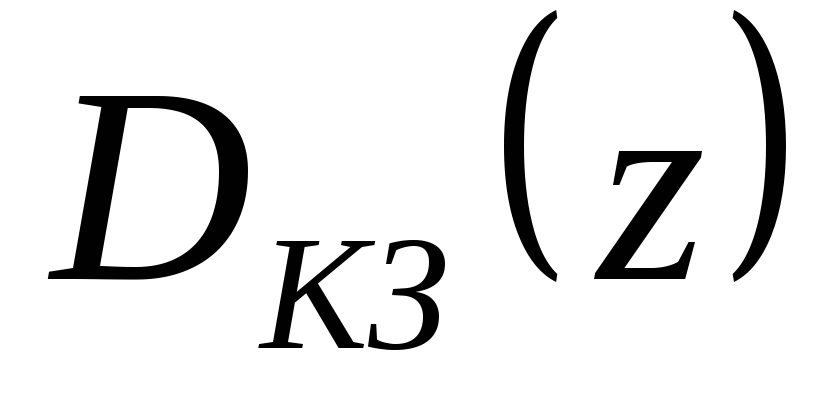 называется иногда методами программирования.
Заданной функции
называется иногда методами программирования.
Заданной функции могут соответствовать различные
программы. Выбор метода программирования
определяется объектом памяти ЦВУ, его
быстродействием, разрядностью и т.д. К
числу основных относятся параллельный,
последовательный и прямой методы
программирования. Последний из них был
использован при реализации дискретного
регулятора для рассматриваемой САУ.
могут соответствовать различные
программы. Выбор метода программирования
определяется объектом памяти ЦВУ, его
быстродействием, разрядностью и т.д. К
числу основных относятся параллельный,
последовательный и прямой методы
программирования. Последний из них был
использован при реализации дискретного
регулятора для рассматриваемой САУ.
Передаточную функцию (10) запишем в виде:
![]() (72)
(72)
где
![]() -
-![]() -изображения
входного и выходного сигналов регулятора.
-изображения
входного и выходного сигналов регулятора.
Следовательно:
![]() (73)
(73)
Выполнив обратное
![]() -
преобразование над обеими частями
последнего выражения, имеем:
-
преобразование над обеими частями
последнего выражения, имеем:
![]()
Из (73) следует, что очередное дискретное
значение выходного регулятора определяется
очередным и двумя предшествующими
значениями входного сигнала, а также
предшествующим значением выходного
сигнала. Алгоритм работы ЦВУ, описываемый
рекуррентным выражением (73), отражен на
структурной схеме, приведенной на рис.
63. В ней
![]() -
элемент задержки сигнала на
-
элемент задержки сигнала на
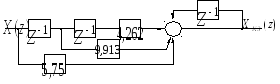
Рис. 63. Структурная схема прямого программирования
передаточной функции![]() (вариант 1)
(вариант 1)
один период квантования. Для реализации такого регулятора требуется три элемента задержки.
При другом варианте прямого метода программирования может быть получен алгоритм работы ЦВУ, отличный от (12).
Согласно (11):
![]() (74)
(74)
Введем фиктивную переменную:
![]() (75)
(75)
Тогда:
![]() (75)
(75)
Выражение (76) преобразуем к виду:
![]() (77)
(77)
На основании (76) и (77) формируется алгоритм управления ЦВУ, предполагающий использование только двух элементов задержки (рис. 64). Соответствующие данному алгоритму рекуррентные зависимости
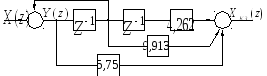
Рис. 64 Структурная схема прямого программирования
передаточной функции![]() (вариант 2)
(вариант 2)