Файл: Конспект лекций для студентов специальности 1 48 01 02 Химическая технология органических веществ, материалов и изделий.docx

H⁰ = – 92 кДж

Реакция экзотермическая, поэтому при увеличении температуры равновесие сдвигается влево, а при понижении температуры – вправо.

Из этого следует, что для увеличения выхода аммиака температуру необходимо понижать. (Почему же тогда синтез аммиака ведут при температуре 500⁰С? – см. раздел «Химическая кинетика»).

Расчет материального баланса в состоянии химического равновесия

Для любой равновесной системы, например 2A  3D + B, расчет материального баланса можно сделать только с применением константы равновесия:

Для любой равновесной системы делается баланс по каждому реагенту с учетом начального его количества, прореагировавшего количества и остатка, участвующего в равновесии. Например, для приведенной выше реакции баланс по веществу А можно записать так: С_нач.(А) = С_р.(А) + [A],

где C_р.(А) – концентрация вещества А прореагировавшего и [A] – его равновесная концентрация.

Веществ B и D – продуктов, до реакции не было, поэтому для них

С_нач.(B) = 0 и С_нач.(D) = 0.

Зная, сколько прореагировало исходного вещества А, можно с помощью уравнения реакции (по соотношению коэффициентов) определить равновесные концентрации продуктов веществ B и D: по уравнению реакции из 2 моль вещества А образуются 1 моль вещества В, поэтому, если прореагировало C_р.(А), то образуется вдвое меньше вещества В, т.е. [B] = 0,5С_р.(А); далее, из 2 моль вещества А образуется 3/2 моль вещества D, тогда [D] = С_р.(А).

Если вещества А прореагировало С_р.(А), то его осталось и участвует в равновесии С_нач.(А) – С_р.(А) = [A].
Различные варианты расчетов материального баланса рассмотрим далее на примере равновесия 2NO + Cl₂  2NOCl.
Пример 1. По равновесным концентрациям реагентов, равным:

[NO] = 2 моль/л, [Cl₂] = 1 моль/л, [NOCl] = 2 моль/л рассчитать начальные концентрации реагентов и константу равновесия.

Решение: на начало реакции продукта NOCl не было, поэтому С_нач.(NOCl) = 0.

Из уравнения реакции видно, что для образования 2 моль/л NOCl должно прореагировать столько же NO (коэффициенты в уравнении одинаковые).

Следовательно, прореагировало NO: С_р(NO) = [NOCl] = 2 моль/л.

Тогда начальная концентрация NO:

---

С_нач.(NO) = [NO] + С_р(NO) = 2 + 2 = 4 моль/л.

Расчет прореагировавшего Cl₂ можно сделать уже двумя вариантами: либо через NOCl (см. выше), либо по прореагировавшему NO:

Из уравнения видно, что если в реакцию вступило С_р(NO), то с ним прореагировало в два раза меньше Cl₂, т.е. С_р(Cl₂) = 0,5С_р(NO) = 0,5·2 = 1 моль/л.

Тогда начальная концентрация Cl₂:

С_нач.(Cl₂) = [Cl₂] + С_р(Cl₂) = 1 + 1 = 2 моль/л.

Рассчитаем константу равновесия:
Пример 2. По заданным начальным концентрациям С_нач.(Cl₂) = 2 моль/л, С_нач.(NO) = 2 моль/л и К = 0,5 рассчитать равновесные концентрации [NO], [Cl₂] и [NOCl] и степень протекания реакции по NO.

Решение: 2NO + Cl₂  2NOCl

Решение данной задачи сводится к тому, чтобы в уравнении константы

равновесия вместо трех неизвестных иметь одно и через него выразить остальные.

Обозначим [NO] = x, и рассчитаем концентрацию прореагировавшего NO: С_р(NO) = С_нач.(NO) – [NO] = С_нач.(NO) – x = 2 – x

Из уравнения реакции видно, что, сколько прореагирует NO, столько же получится NOCl, и это его равновесная концентрация, т.е. [NOCl] = 2 – x

Из уравнения реакции видно, что хлора прореагирует в 2 раза меньше, чем NO, т.е. С_р(Cl₂) = 0,5С_р(NO) = 0,5(2 – x) = 1 – 0,5x.

Тогда [Cl₂] = 2 – (1 – 0,5x) = 1 + 0,5x

Из константы равновесия рассчитаем [NO] = x:

; откуда x = 1,1 моль/л

Таким образом:

[NO] = 1,1 моль/л, [Cl₂] = 1 + 0,5x = 1,55 моль/л,

[NOCl] = 2 – x = 0,9 моль/л

Степень протекания реакции по NO:

α = С_р(NO)/С_нач.(NO) = (С_нач.(NO) – [NO])/С_нач.(NO) = (2 – 1,1)/2 = 0,45

α = 0,45 или 45 %.

---

4.4 Основы химической кинетики

Химическая кинетика – учение о химическом процессе, его механизме и закономерностях протекания во времени.

Химическая кинетика наряду с химической термодинамикой – теоретическая основа химической технологии, поскольку позволяет оптимизировать и интенсифицировать промышленно важные реакции. Тепловой эффект реакции, преимущественное направление и глубина ее протекания определяются законами термодинамики; однако из них совсем не следует возможность прогнозирования скорости перехода из начального в конечное состояние, а также через какие промежуточные стадии проходит это превращение.

Пример: H_2(г) + 1/2O_2(г)  H₂O(г) H⁰ = – 242 кДж/моль

NO_(г) + 1/2O_2(г)  NO_2(г) H⁰ = – 56 кДж/моль

Первая реакция энергетически более выгодна, однако скорость ее несравнимо меньше, чем второй реакции.
Основные понятия и определения

Механизм химической реакции – совокупность элементарных стадий, из которых складывается химическая реакция.

Элементарной называют реакцию, которая осуществляется превращением реагентов в продукты реакции в одну стадию.

Молекулярность реакции – число частиц (молекул, атомов, радикалов, ионов), участвующих в элементарном акте химической реакции. Различают мономолекулярные реакции (в элементарном акте участвует одна молекула), например, реакции изомеризации или разложения:

2N₂O_5(г) = 4 NO_2(г) + O_2(г)

– бимолекулярные реакции, в которых две молекулы участвуют в образовании одного или нескольких веществ, например, реакции соединения или обмена (А + B = С, AB + CD = AD + BC): C₂H₄ + HI = C₂H₅I

– тримолекулярные реакции, которые протекают при одновременном столкновении трех молекул (встречаются довольно редко):

2NO + Cl₂ = 2NOCl

Реакции более чем тримолекулярные практически не встречаются.


А

В
Скорость химической реакции – это число элементарных актов химического взаимодействия, протекающих в единицу времени в единице объема (для гомогенных реакций) или на единице поверхности (для гетерогенных реакций) – это абсолютная скорость. Для реакций, даже очень медленных, абсолютная скорость огромна. Например, если из одного моля вещества за секунду реагирует 1/1000000000 часть молекул, то это составляет (вспомните число Авогадро) 10

---

¹⁵ молекул. Поэтому на практике определяют не абсолютную скорость реакции, а ее результат – изменение количества или концентрации вещества за единицу времени. При этом различают мгновенную и среднюю скорости реакции.

Мгновенная скорость – это скорость на определенное время (короткое мгновение): V = ± dС/dt

(если скорость контролируется по образующемуся продукту, то знак «+», если по расходу исходного реагента, то «–»)

Среднюю скорость определяют по изменению количества ( n) или концентрации ( C) вещества за определенный временной интервал ( t):
Vср. = ± С/ t
По результатам измерений концентраций во времени строят так называемые кинетические кривые. Например, в ходе реакции А  В концентрация реагента А уменьшается, а реагента В – увеличивается (рисунок 4.4.1).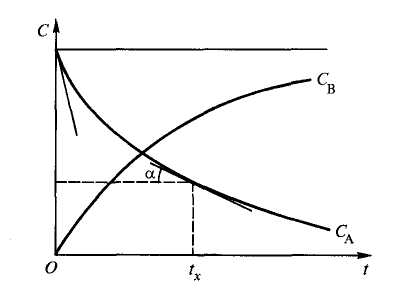


Рисунок 4.4.1 – Типичные кинетические кривые для исходного вещества А и продукта реакции В
С помощью кинетической кривой можно графически определитьмгновенную скорость, в момент времени t_х: для этого потребуется восстановить перпендикуляр от оси абсцисс в т. t_x до пересечения его с кинетической кривой и провести касательную к точке пересечения. Тангенс угла наклона касательной и есть мгновенная скорость (V = dс/dt).
Влияние концентраций реагирующих веществ на скорость химической реакции. Закон действующих масс

Зависимость скорости реакции от концентрации реагирующих веществ показывает кинетическое уравнение (уравнение кинетической кривой).

Например, для условной реакции aA + bB  dD + fF кинетическое уравнение можно представить в следующем виде:

V = kСx(A)Сy(B)

(4.4.1)

---

Уравнение (4.4.1) часто называют законом действующих масс, который для элементарных реакций сформулировали К.Гульдберг и П.Вааге.

Коэффициент k, входящий в уравнение (4.4.1), называют константой скорости реакции. Константа скорости реакции зависит от природы реагирующих веществ и температуры. Поскольку k = V при С = 1 моль/л, то ее иногда называют удельной скоростью.

Обратите внимание на то, что в большинстве случаев стехиометрические коэффициенты в уравнении реакции не отражают истинного механизма реакции. По этой причине показатели степеней (x, y) при концентрациях в уравнении (4.4.1) очень редко соответствуют стехиометрическим коэффициентам (в отличие от закона действующих масс применительно к химическому равновесию).

Показатели степеней x, y при концентрациях реагентов А и В в уравнении (4.4.1) называют порядком реакции по веществу А и веществу В, соответственно, а сумму (x + y) называют общим порядком реакции.

Порядок химической реакции, как по отдельным реагентам, так и общий, определяют экспериментально. По этим данным составляют кинетические уравнения. В зависимости от суммы (x + y) различают реакции нулевого, первого, второго или третьего порядка. (Реакции более высоких порядков не встречаются; поэтому в случае, если сумма стехиометрических коэффициентов в уравнении реакции превышает три, то это заведомо многостадийная реакция).

Скорость большей части реакций описывается кинетическим уравнением первого порядка: dС/dt = kt или в интегральной форме:

С = С0exp(–kt)

(4.4.2)

Если интересен расчет не концентрации на определенное время t, а изменение концентрации, то уравнение (4.4.2) преобразуют в более удобное:

ln(С0/С) = kt

(4.4.3)

Время полуреакции (t½) – это время, за которое количество вещества (или число его частиц, или масса, или его молярная концентрация) уменьшается вдвое. Из уравнения (5) легко вывести, что при с₀/c = 2

t½ = ln2/k = 0,693/k

(4.4.4)

Определение времени полуреакции – это один из

---