Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc

3.2.Алгебраический критерий устойчивости Гурвица

Для оценки устойчивости линейной системы по критерию Гурвица необходимо из коэффициентов характеристиче­ского уравнения (3.5) составить определитель Гурвица, размерность которого равна порядку системы.

Определитель Гурвица имеет вид:

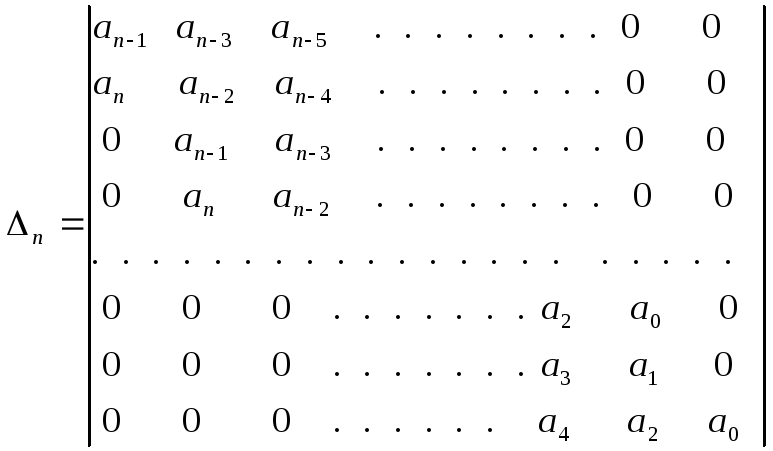. (3.8)

Порядок составления определителя Гурвица следующий. В качестве элемента первого столбца первой строки определителя записывается коэффици­ент a_n-1, а затем на главной диагонали располагаются коэффициенты характеристического уравнения (3.4) с последовательно убывающими индексами. При этом в последнем столбце последней строки определителя записывается коэффициент .

Затем, начиная от коэффициентов, стоящих на главной диагонали, заполняются столбцы определителя так, чтобы ин­дексы коэффициентов, расположенных над коэффициентами главной диагонали, последовательно убывали, а коэффициентов, расположенных под диагональными коэффициентами, – последовательно возрастали. Если в процессе заполнения столбца определителя индекс коэффициента достигает значения n или 0, то дальнейшее заполнение столбца осуществляется нулями.

Далее необходимо вычислить значение определителя Гурвица и всех его диагональных миноров, которые получают из определителя (3.8) путем отчеркивания равного числа строк и столбцов в левом верхнем углу определителя. Например, диагональный минор первого порядка равен Δ₁ = a_n-1 ; диагональный минор второго порядка:

Δ₂ =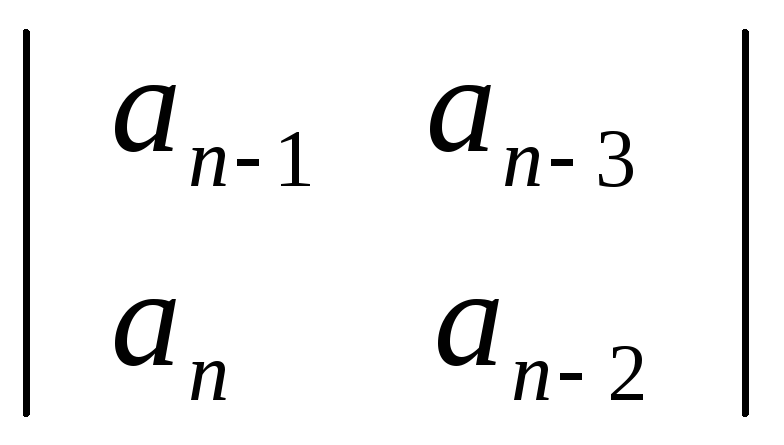, (3.9)

а диагональный минор третьего порядка:

Δ₃ = 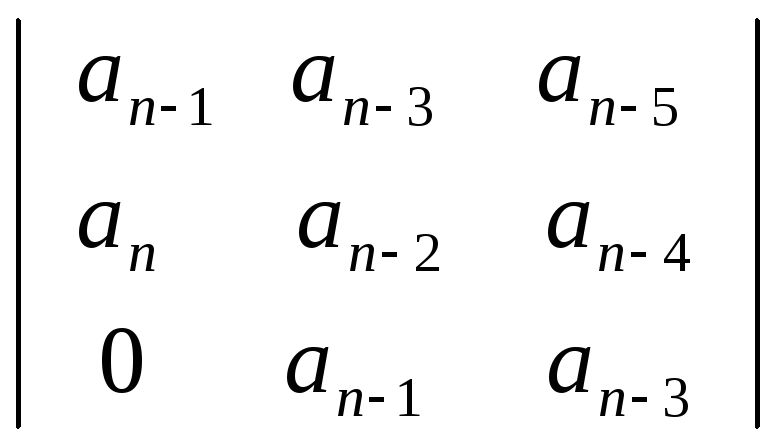. (3.10)

Очевидно, что диагональный минор n-го порядка совпадает с определителем Гурвица.

Линейная система устойчива, если при выполнении необходимого условия (3.6), определитель Гурвица и все его диагональные миноры будут положительны:

Δ₁ > 0, Δ₂ > 0, …………,Δ_n > 0/

Раскрыв определитель Гурвица по последнему столбцу, получим

Так как, в соответствие с выражением (3.6) > 0 и > 0, то для проверки устойчивости систе­мы достаточно уточнить знаки диагональных миноров с номерами от второго до .

Для системы второго порядка необходимое и достаточное условия устойчивости совпадают, так как для нее Δ₁ = a₁ > 0 .

Для системы третьего порядка:

Δ₁ = a₂ > 0; Δ₂ = а₁ ∙а₂ – а₀ ∙а₃.

Следовательно, достаточное условие устойчивости:

а₁ ∙а₂ > а₀ ∙а₃. (3.11)

Если определитель Δ_n = 0, то САУ находится на границе устойчивости. При этом возможны два случая:

1. сво­бодный член характеристического уравнения равен нулю, т.е. a₀ = 0, что соответствует нейтрально устойчивой системе;

2. диагональный минор Δ_(n-1) = 0, что соответствует колебательной границе устойчивости.

Из условия Δ_(n-1) = 0 можно опреде­лить параметры, при которых САУ находится на границе устойчивости.

Рассмотрим в качестве примера замкнутую систему третьего порядка с единичной отрицательной обратной связью и передаточной функцией в разомкнутом состоянии:

.

Передаточная функция такой системы в замкнутом состоянии в соответствие с выражением (2.63) равна:

.

Характеристическое уравнение такой системы:

T₁T₂T₃ p³ + (T₁T_{2 +} T₂T_{3 +} T₁T₃)р² + (T_{1 +} T_{2 +} T₃)р + (k + 1) = 0.

Следовательно:

= T₁T₂T₃ , T₁T_{2 +} T₂T_{3 +} T₁T₃ , а₁ = T_{1 +} T_{2 +} T3 , а₀ = k + 1. (3.12)

В соответствии с выражениями (3.6) и (3.11) необходимое и достаточное условия устойчивости для системы третьего порядка определяются следующими неравенствами:

T₁T₂T₃ > 0; T₁T_{2 +} T₂T_{3 +} T₁T₃ > 0; T_{1 +} T_{2 +} T3 > 0; k + 1 > 0;

(T₁T_{2 +} T₂T_{3 +} T₁T₃)∙(T_{1 +} T_{2 +} T₃) > T₁T₂T₃ ∙(k + 1).

Очевидно, что первые три неравенства выполняются при произвольных положительных значениях коэффициента усиления и постоянных времени. Последнее неравенство ограничивает сверху допустимое значение коэффициента усиления:

k < (T_{1 +} T_{2 +} T₃ )∙(1/ T₁ + 1/ T₂ + 1/ T₃) – 1 .

Предельное значение k, при котором система будет находиться на границе устойчивости, –критическое значение для рассматриваемой системы равно:

k_кр = (T_{1 +} T_{2 +} T₃ )∙(1/ T₁ + 1/ T₂ + 1/ T₃) – 1.

Существенным недостатком критерия Гурвица является значительное усложнение условий устойчивости по мере увеличения порядка системы. Кроме того, для САУ высокого порядка достаточно трудно оценить влияние отдельных параметров звеньев на устойчивость системы. Это связано с тем, что, как правило, одни и те же параметры одновременно входят в несколько коэффициентов характеристического уравнения (смотри, например, выражение (3.12)).

3.3.Частотные критерии устойчивости Михайлова и Найквиста

Частотные критерии устойчивости основываются на использовании принципа аргумента. Рассмотрим этот принцип, для чего характеристический полином замкнутой системы

(3.13)

в соответствие с теоремой Безу представим в виде:

F(p) = , (3.14)

где p_i – полюс передаточной функции замкнутой системы ().

Поставляя в выражение (3.13) вместо p комплексную переменную jω, получим:

. (3.15)

После аналогичной подстановки в выражение (3.14) получим:

F( jω) = . (3.16)

Каждому сомножителю в выражении (3.16) на комплексной плоскости соответствует некоторый вектор, положение которого меняется при изменении ω.

Определим изменение аргумента комплексной функции F(jω) при изменении частоты ω от 0 до . Для этого необходимо определить изменение аргумента каждого из векторов, поскольку

F(jω) = ∑(jω – p_i).

Если корень характеристического уравнения p_i действительный и отрицательный, т.е. рас­положен на действительной оси слева от начала координат (рис. 3.4, а), то вектор поворачивается против часовой стрелки на угол π/2, если этот ко­рень действительный и положительный (рис. 3.4, б), то вектор поворачивается по часовой стрелке на угол π/2. Следовательно, для левого действительного полюса

= π/2,

а для правого действительного полюса

= – π/2,

Нетрудно показать, что для пары комплексно сопряженных левых полюсов (рис. 3.4, в) изменение аргумента составляет +π, а для пары комплексно сопряженных правых полюсов (рис. 3.4, г) равно -π.

Если среди n полюсов передаточной функции замкнутой системы m расположены справа от мнимой оси, а остальные (n – m) – слева, то изменение аргумента комплексной функции F(jω) вектора равно:

F(jω) = (n – m)∙ π/2 – m∙π/2 = (n – 2m)∙π/2. (3.17)

Выражение (3.17) и определяет суть принципа аргумента. В передаточной функции устойчи­вой системы правые полюса отсутствуют, т.е. m = 0, и изменение аргумента F(jω) равно:

F(jω) = n∙π/2. (3.18)

Из выражения (3.18) следует критерий устойчивости Михайлова, согласно которому из­менение аргумента комплексной функции F(jω) определяется по годографу, который записывают в виде

F(jω) = Х(ω) + jY(ω) ,

где Х(ω),Y(ω) – действительная и мнимая составляющие комплексной функции F(jω);

Х(ω) = a₀ – a₂ω² + a₄ω⁴ – a₆ω⁶ + ……;

Y(ω) = a₁ω – a₃ω³ + a₅ω⁵ – a₇ω⁷ + …….

Каждому значениюω = ω_i на комплексной плоскости соответствует точка с координатами ( Х(ω_i),Y(ω_i) ). При изменении ω эта точка описывает на плоскости некоторую траекторию, которая называется годографом Михайлова (рис. 3.5).

При ω = 0 Х(0) = a₀, Y(0) = 0, т.е. F(0) = a₀, причем в соответствии с выражением (3.6) a₀ > 0.

Формулировка критерия Михайлова: замкнутая система устойчива, если годограф F(jω), начинаясь при ω = 0 на положительной дей­ствительной полуоси, при изменении ω от 0 до обходит последовательно в положитель­ном направлении (против часовой стрелки)n квадрантов, где n – порядок системы.