Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc

2.3. Временные и частотные характеристики звеньев и систем

Динамические свойства линейных звеньев и систем автоматического управления в целом могут быть описаны дифференциальными уравнениями и передаточными функциями, а также с помощью временных и частотных характеристик. Временная характеристика представляет собой функцию времени, описывающую выходной сигнал звена (или системы) при подаче на вход звена определенного тестирующего сигнала. Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.

У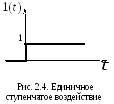казанные характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида. Переходные и частотные характеристики однозначно связаны с дифференциальным уравнением звена и его передаточной функцией и наряду с ними являются исчерпывающим описанием динамических свойств звена.

К числу основных временных характеристик звена или системы относятся переходная функция и функция веса.

Переходная функция звена представляет собой сигнал на выходе звена (реакцию звена), вызванный подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция, функция Хевисайда) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным (рис. 2.4). Единичное ступенчатое воздействие обозначается и может быть описано следующим выражением:

(2.20)

Переходная функция обычно обозначается . Следовательно,– это выражение дляпри=.

Наряду с переходной функцией при описании звеньев и систем применяется функция веса, общепринятое обозначение которой . Эта временная характеристика представляет собой реакцию звена надельта-функцию (единичную импульсную функцию, иглу Дирака). Дельта-функция, которая обозначается , – это математическая идеализация предельно короткого импульсного сигнала бесконечно большой амплитуды. Математически дельта-функцию можно описать следующим образом:

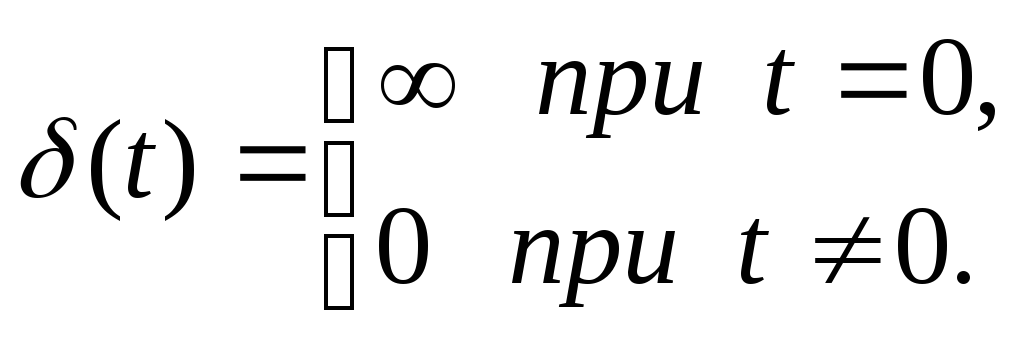(2.21)

При этом согласно определению дельта-функции

. (2.22)

Таким образом, - этопри=.

Поскольку дельта-функция равна производной по времени от единичного ступенчатого воздействия, то и между переходной функцией, и функцией веса линейных звеньев существует аналогичная связь:

. (2.23)

И наоборот

.

Зная переходную и функцию веса, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:

; (2.24)

, (2.25)

где ,– значенияиприt = 0;

Выражения (2.24) и (2.25) легко получаются друг из друга, являясь вариантами интеграла Дюамеля или интеграла свертки. У реальных инерционных звеньев и систем h(0)=0, так как реакция на их выходе всегда отстает от входного воздействия. Поэтому в дальнейшем выражения (2.24) и (2.25) приводятся без первого слагаемого.

Временные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразований Лапласа.

Поскольку , в случае, когда входное воздействие (t) представляет собой единичный импульс , и с учетом того, что его изображение по Лапласу, получим следующее выражение для изображения функции веса звена:

w(p) =W(p) или , т.е.

. (2.26)

Таким образом, функция веса определяется через передаточную функцию по формуле обратного преобразования Лапласа, т.е. является ее оригиналом.

В случае, когда (t) = 1(t), учитывая, что L = 1/p, получаем следующее выражение для изображения переходной характеристики:

Следовательно, переходная характеристика звена равна:

При рассмотрении частотных характеристик считаем, что на входе системы дейст­вует гармонический сигнал с амплитудой и часто­той:

. (2.27)

По окончании переходного процесса на выходе линейной системы будут существовать гармонические колебания с той же частотой, что и у входного сигнала, но в общем случае отличающиеся от него по амплитуде и фазе, т.е. в установившемся режиме выходная величина звена равна:

, (2.28)

где – амплитуда установившихся выходных колебаний;– фазовый сдвиг между входными и выходными синусоидальными колебаниями.

При изменении частоты изменяется, как соотношение между амплитудами входных и выходных колебаний, так и фазовый сдвигмежду ними. При этом зависимость от частоты отношения амплитуд называетсяамплитудно-частотной характеристикой (АЧХ), т.е.

.

Зависимость величины фазового сдвига от частоты называетсяфазо-частотной характеристикой (ФЧХ).

Определив амплитудно- и фазо-частотную характеристики системы, например, получив их экспериментально, можно построить еще одну частотную характеристику – амплитудно-фазовую (АФЧХ).

Амплитудно-фазовую характеристику, используя в качестве полярных координат, строят на комплексной плоскости по следующим правилам. Задаются значением частотыω_i, для которого по графику ФЧХ определяют величину фазового сдвига φ(ω_i) , а по графику АЧХ – величину A(ω_i).

Из начала координат комплексной плоскости проводится луч под угломφ(ω_i) к положительной действительной полуоси. Угол откладывается против часовой стрелки, если φ(ω_i) > 0, т.е. когда выходной гармонический сигнал опережает входной, и в противоположном направлении, если φ(ω_i) < 0 .Из начала координат по этому лучу откладывается отрезок, длина которого в выбранном масштабе равна A(ω_i) (рис. 2.5, в).

Каждая точка амплитудно-фазовой частотной характеристики соответствует определенному значению частоты. Значения для конечного количества точек характеристики наносятся вдоль характеристики и указывают направление возрастания частоты ω.

Очевидно, что возможно и решение обратной задачи: по годографу амплитудно-фазовую частотную характеристику можно построить характеристики и. На рис. 2.5 приведен примерный вид этих характеристик для инерционной системы.

Как показано на этих рисунках, у таких звеньев в силу их инерционности амплитудная частотная характеристика по мере увеличения частоты в конце концов спадает до нуля. При этом, чем менее инерционно звено, тем шире его амплитудная частотная характеристика, т.е. тем больше полоса пропускаемых звеном частот, или просто его полоса пропускания.

Теоретически частотная характеристика продолжается до бесконечности, но практически полоса пропускания оценивается значением частоты, при котором отношение амплитуд окончательно становится меньше определенного, достаточно малого конечного значения. Это значение обычно берут равным 0,05 (на этой частоте амплитуда выходных колебаний падает до 5 % амплитуды входных колебаний). Наличие максимума у амплитудной частотной характеристики говорит о резонансных свойствах звена. Частота, соответствующая максимуму амплитудной характеристики, называется резонансной ().

Фазовая характеристика у обычных инерционных звеньев (рис. 2.5, б) отрицательна ((ω)< 0), т.е. выходные колебания отстают по фазе от входных, и это отставание растет с частотой.

Используя символическую форму записи гармонических сигналов x_вх(t) и x_вых(t), получим аналитические выражения для рассмотренных характеристик, их зависимость между собой и с передаточной функцией системы.

Символическая запись сигналов (2.27) и (2.28):

, .

Определим амплитудно-фазовую характеристику системы, как отношение выходного сигнала системы к входному, выраженное в комплексной форме:

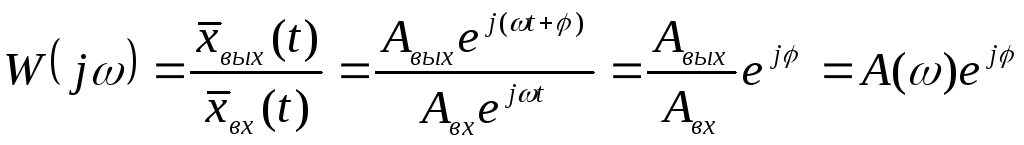. (2.29)

Из выражения (2.29) следует, что амплитудно-частотная и фазо-частотная характеристики является соответственно модулем и фазой (аргументом) амплидудно-фазовой характеристики: