Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc

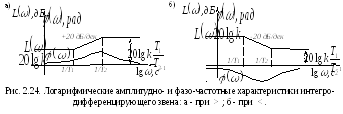Графики логарифмической амплитудно- и фазо-частотной характеристик приведены на рис. 2.24. Очевидно, что при>в среднечастотном диапазоне преобладают дифференцирующие свойства звена (наклон ЛАХ +20дБ/дек), а при<– интегрирующие свойства (наклон ЛАХ -20 дБ/дек).

Воспользуемся формулой разложения (2.15) для получения выражение переходной функции интегро-дифференцирующего звена.

Изображение по Лапласу переходной функции:

В соответствии с выражением (2.15):

; ;;

; ;;;

Следовательно, переходная функция интегро-дифференцирующего звена (рис. 2.25) имеет вид:

Пропорционально-интегральный регулятор (пи-регулятор)

Пропорционально-интегральный регулятор (ПИ-регулятор) – это звено, зависимость между выходным и входным сигналами которого описывается следующим дифференциальным уравнением:

Операторное уравнение звена:

Передаточная функция звена

Следовательно, изображение по Лапласу сигнала на выходе звена представляет собой сумму двух составляющих, одна из которых пропорциональна входному сигналу, а вторая – пропорциональна интегралу от входного сигнала, что и определяет название данного звена:

Частотные характеристики ПИ-регулятора:

; ;

Г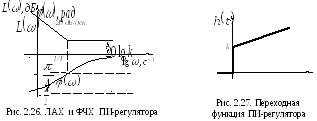рафики логарифмических амплитудно- и фазо-частотной характеристик звена приведены на рис.2.26.

Переходная функция звена (рис. 2.27):

2.5. Неминимально-фазовые звенья

Мы рассмотрели наиболее часто встречающиеся на практике типы минимально-фазовых звеньев. В отличие от них передаточная функция любого неминимально-фазового звена имеет хотя бы один «правый» ноль или полюс. Приведем пример такой передаточной функции:

Здесь имеется положительный полюс (корень знаменателя):

Частотные характеристики такого звена:

; ,

так как при входной и выходной гармонические сигналы находятся в противофазе.

В то же время для обычного апериодического звена имеем:

Разница между ними, как видим, в величине фазы, амплитудные же характеристики одинаковы. Оказывается, что из всех возможных звеньев с одинаковыми амплитудными характеристиками минимально-фазовые типовые звенья обладают наименьшими по абсолютному значению фазовыми характеристиками. В этом и состоит смысл введенных терминов.

Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудно-частотной характеристике всегда можно определить амплитудно-фазовую и наоборот. Этим же свойством обладают вещественная и мнимаячасти амплитудно-фазовой характеристики минимально-фазовых звеньев.

Заметим, что для данного неминимально-фазового звена переходная функция будет расходящейся, вместо обычной затухающей.

2.6. Эквивалентные преобразования структурных схем линейных сау

В САУ встречаются три вида соединений звеньев: последовательное, параллельное и соединение звеньев по схеме с обратной связью.

В системе, состоящей из n последовательно соединенных звеньев (рис. 2.28) выходной сигнал предыдущего звена равен входному сигналу последующего.

И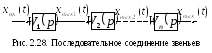зображения по Лапласу выходных сигналов этих звеньев равны:

x_вых1(p) = W₁(p)x_вх(p); x_вых₂(p) = W₂(p) x_вых₁(p); … x_вых(p) = W_n(p)x_вых(_n₎(p).

Откуда

x_выхx_вх(p).

Следовательно, передаточная функция системы примет вид:

. (2.57)

Таким образом, передаточная функция последовательно соединенных звеньев равна произведению передаточных функций этих звеньев.

Частотные характеристики последовательно соединенных звеньев:

где A(ω) = A₁(ω)A₂(ω)…A_n(ω); .

Логарифмическая амплитудно-частотная характеристика звеньев, соединенных последовательно:

.(2.58)

Следовательно, логарифмические амплитудно- и фазо-частотная характеристики системы, состоящей из последовательно соединенных звеньев, равны сумме ЛАХ и ФЧХ отдельных звеньев. Это существенно упрощает построение логарифмических частотных характеристик, по сравнению с обычными характеристиками.

Передаточная функция минимально-фазовой системы в общем случае может быть записана в виде:

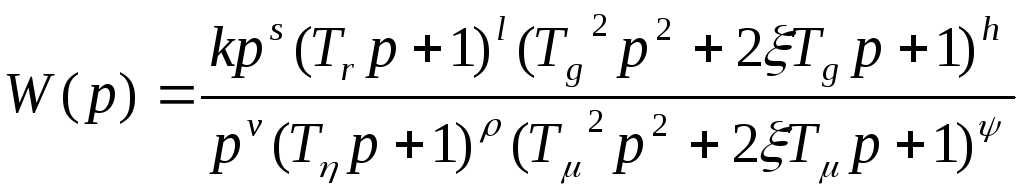. (2.59)

В выражении (2.59) сомножители в числителе определяют нули передаточной функции, а именно:

сомножитель соответствует нулевому нолю кратности,
сомножитель – действительному нолю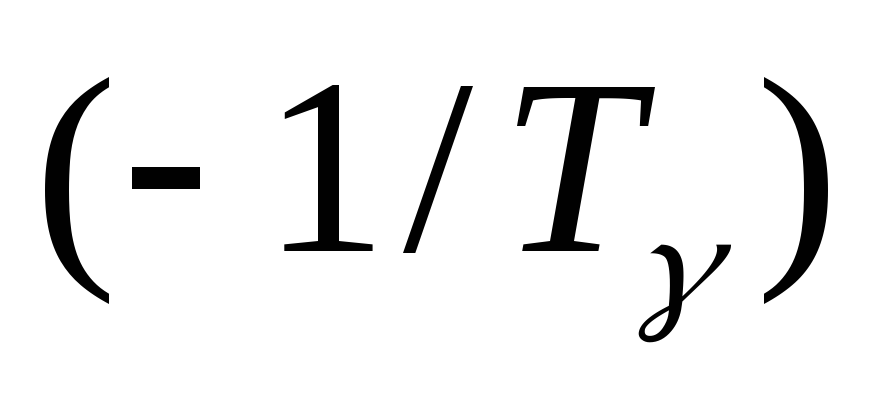кратностиl,
сомножитель 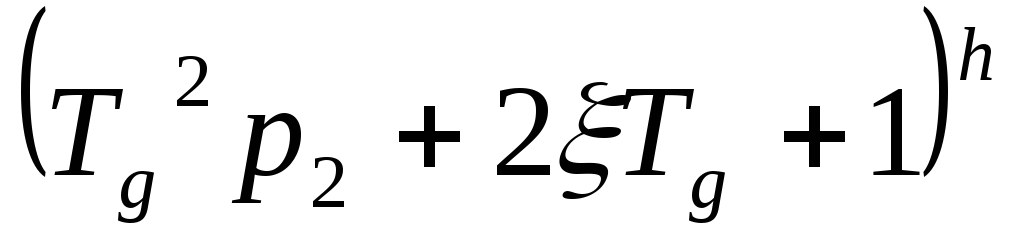– паре комплексно-сопряженных нолей кратности .

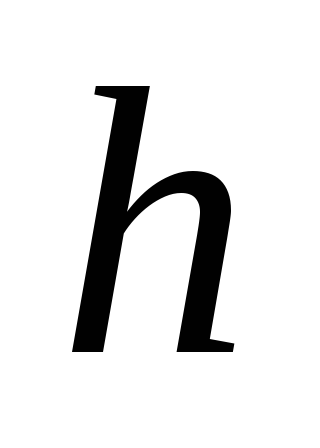Аналогичные сомножители в знаменателе выражения (2.59) определяют полюса передаточной функции, а именно:

сомножитель 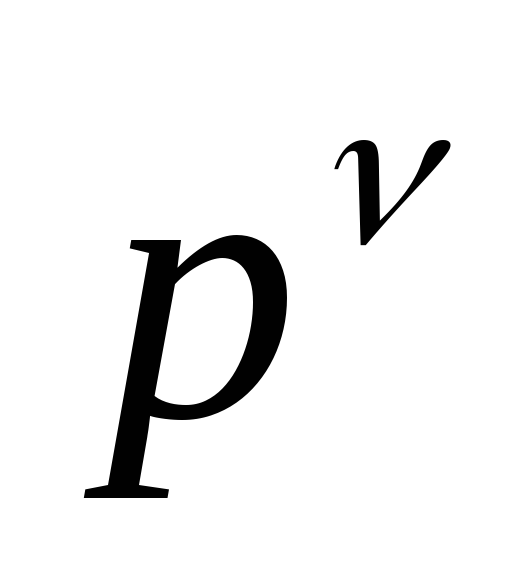соответствует нулевому полюсу кратности,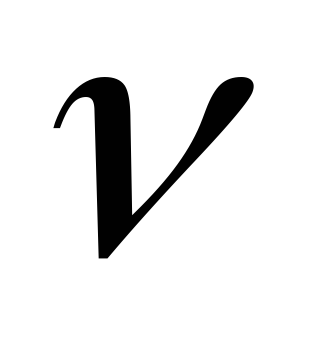
сомножитель 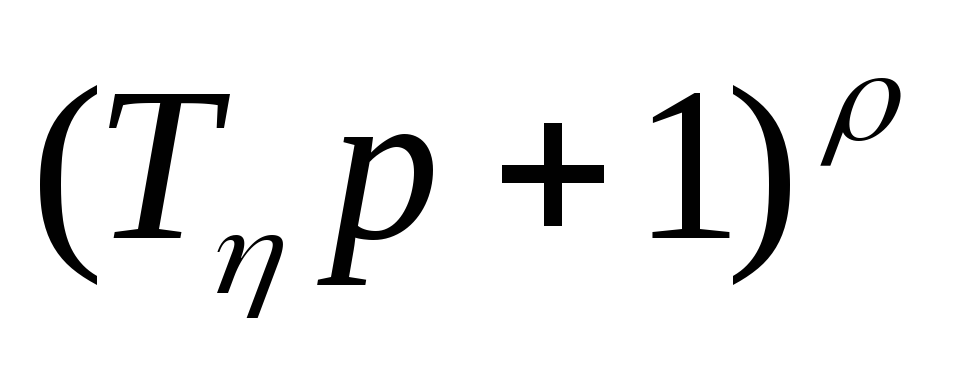– действительному полюсу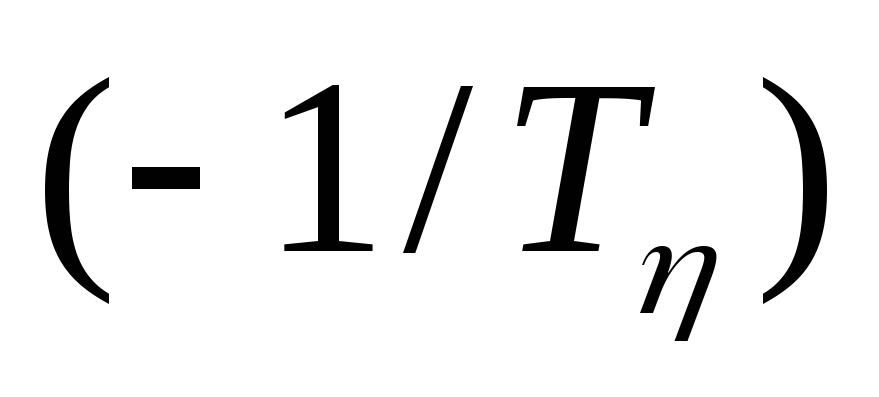кратности,
сомножитель 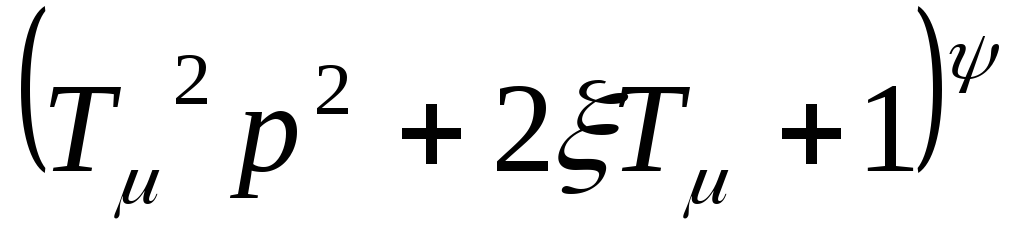– паре комплексно-сопряженных полюсов кратности .

Очевидно, что в зависимости от соотношения s и передаточная функция (2.59) может иметь только один тип особенностей: либо нулевые ноли, либо нулевые полюса. Кроме того, предполагается, что в (2.59) для коэффициентов демпфирования выполняются неравенства: 0 <ζ < 1.

Формально передаточная функция (2.59) представляет собой произведение нескольких сомножителей, что соответствует последовательному соединению звеньев, и для вычисления можно воспользоваться выражением (2.58). При этом построение ЛАХ системы осуществляется без предварительного построения ЛАХ отдельных звеньев по следующим правилам.

Смотрите также файлы

Г.М. Гринфельд лекции по курсу дискретные системы автоматического управления.doc

Экологический аудит лекции.doc

Экологический аудит 4 лекции.docx

Экологический аудит 3 лекции.doc

Экологический аудит 2 лекции.doc

Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc

Пропорционально-интегральный регулятор (пи-регулятор)

2.5. Неминимально-фазовые звенья

2.6. Эквивалентные преобразования структурных схем линейных сау

Смотрите также файлы

Информация

Списки файлов

Дополнительно