Файл: Контрольная работа состоит из решения 10 практических заданий.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 172
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 5
В банк сделан вклад в размереP = 850 000 рублей сроком на n = 10 лет под i = 10,0% годовых. Проценты начисляются по схеме сложного процента. Проценты начисляются два раза в месяц.
За указанный период времени среднегодовой уровень инфляции составил
Определить:
1) реальную наращенную сумму за указанный период времени;
2) реальную годовую процентную ставку;
3) компенсирующую годовую процентную ставку указанной операции, соответствующую данному уровню инфляции;
4) обеспечивающую годовую процентную ставку указанной операции, для реальной доходности 10,0% в год при данном уровне инфляции.
Решение:
Определим сначала сумму вклада к концу срока наращения (начисления раз в полгода, m = 2):
Рассчитываем реальную наращенную сумму за указанный период времени:
Рассчитываем реальную годовую процентную ставку:
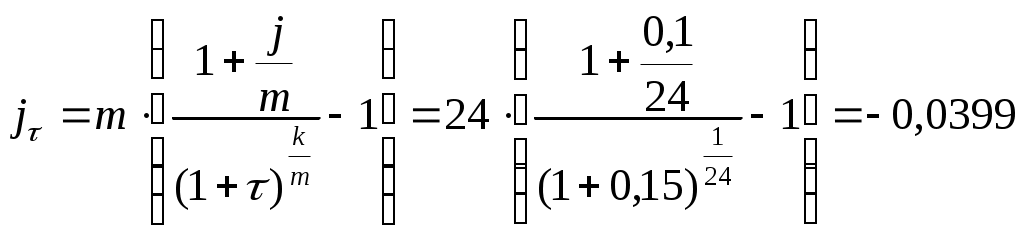 или -3,99%
или -3,99%Так как реальная наращенная сумма (569 944,71 руб.) оказалась ниже суммы вклада (850 000 руб.), то и реальная процентная ставка оказалась отрицательной. Процесс обесценивания денег за счет инфляционных процессов идет происходит интенсивнее, чем начисление процентов по вкладу.
Определим обеспечивающую годовую процентную ставку указанной операции, для реальной доходности i= 10,0%
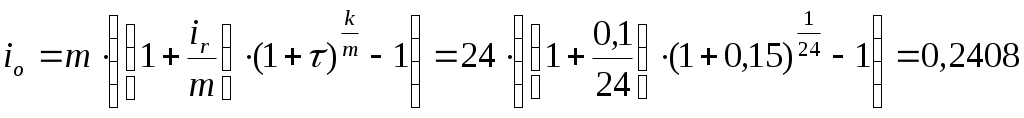
Определим компенсирующую ставку:
Таблица 4
Основные результаты решения Задания 5
| Определяемая величина | Значение |
| Реальная наращенная сумма, руб. | 569 944,71 |
| Реальная годовая процентная ставка, % | -3,99 |
| Компенсирующая годовая процентная ставка, % | 14,02 |
| Обеспечивающая годовая процентная ставка, % | 24,08 |
Задание 6
У предпринимателя есть ценная бумага, гарантирующая выплату по ней в размере P = 850 000 рублей через n = 10 лет. Предприниматель, желая получить деньги прямо сейчас, переуступает это обязательство банку. Банк согласен принять данную ценную бумагу с дисконтом i= 6,4% годовых.
Определить, какая сумма будет выплачена предпринимателю, если дисконтирование будет осуществлено по следующим схемам:
а) по правилу математического дисконтирования с простым процентом;
б) по правилу математического дисконтирования со сложным процентом;
в) по правилу банковского учета с простым процентом;
г) по правилу банковского учета со сложным процентом.
Решение:
а) Находим дисконтированную сумму по правилу математического дисконтирования с простым процентом
б) Находим дисконтированную сумму по правилу математического дисконтирования со сложным процентом
в) Находим дисконтированную сумму по правилу банковского учета с простым процентом
г) Находим дисконтированную сумму по правилу банковского учета со сложным процентом
Результаты расчетов представлены в таблице 5:
Таблица 5
Основные результаты решения Задания 6
| Процент/Дисконтирование | Математическое | Банковский учет |
| Простой | 518 292,68 | 306 000,00 |
| Сложный | 457 090,97 | 438 709,88 |
Задание 7
У финансовой организации есть три варианта долгосрочного вложения средств:
ВАРИАНТ 1 – вложить денежные средства в размере Р1= 850 000 руб. на n1= 10 лет в банк под i1 = 10,0% годовых с ежеквартальным начислением процентов;
ВАРИАНТ 2 – вложить средства в размере Р2= 560 000руб. на n2 = 11 лет в проект, который принесет в конце срока не облагаемый налогом доход Q2 = 1 140 000рублей;
ВАРИАНТ 3 – вложить денежные средства в размере P3 = 100 000 рублей на n3 = 13 лет в бизнес, который принесет в конце срока доход Q3 = 420 000рублей, но нужно будет заплатить налог g3 = 9,5% со всего полученного дохода.
Определить, какой из вариантов вложения средств наиболее выгоден для предпринимателя, если операции оцениваются по правилу сложного процента. Вывод обосновать.
Решение:
Сравнение долгосрочных финансовых операций проводится на основе сравнения их эффективных процентных ставок, определенных для метода сложных процентов.
Рассчитываем наращенную сумму для 1-го варианта:
Рассчитываем эффективную ставку процента для 1-го варианта:
Рассчитываем эффективную ставку процента для 2-го варианта:
Для 3-го варианта рассчитываем разницу между наращенной суммой и вкладом, т.е. сумму дохода от финансовой операции:
420 000 – 100 000 = 320 000 (руб.)
Рассчитываем сумму налога с дохода от операции:
320 000 ∙ 0,095 = 30 400 (руб.)
Рассчитываем наращенную сумму после выплаты процентов:
420 000 – 30 400 = 389 600 (руб.)
Рассчитываем эффективную ставку процента для 3-го варианта:
Если налогом облагается полностью наращенная сумма, а не только сумма чистого дохода от операции, то наращенная сумма за вычетом налога составит: 420 000 – 420 000×0,095 = 380 100 руб.
Рассчитываем эффективную ставку процента для 3-го варианта, когда налогом облагается полностью наращенная сумма:
Чем выше годовая эффективная ставка, тем экономически выгоднее вариант вложения средств для финансовой организации. Наибольшая годовая эффективная ставка реализуется в 3-м варианте. Именно его и нужно выбрать финансовой организации.
Задание 8
Государство Y просит в долг у государства X денежную сумму в размере P = 40 млрд. €. По взаимной договоренности установлена процентная ставка кредитной операции в размере i = 6%.
Согласно договору займа, долг должен быть возвращен двумя платежами: R1 = 30 млрд. € черезn1= 4 года год и R2млрд. € через n2 = 6 лет.
1) Определить, какова должна быть сумма 2-го платежа R2, при известной сумме 1-го платежа R1 = 30 млрд. €.
Первый платеж выполнен вовремя и в полном объеме. Но к моменту второго платежа в государстве Y разразился экономический кризис, и оно настаивает на реструктуризации выплат. На переговорах государство-заемщик Y предлагает государству-кредитору X два варианта реструктуризации:
ВАРИАНТ 1. Единым платежом в размере D = 18 млрд. € с переносом его на момент времениn3 = 10 лет от даты взятия в долг.
ВАРИАНТ 2. Двумя равными платежами в размере S = 8 млрд. €, один в указанный в договоре момент времени n2 = 6лет от даты взятия в долг, а второй в момент времени n3 = 10лет от даты взятия в долг.
Государство-кредитор X вынуждено согласиться с каким-либо вариантом, иначе оно рискует не получить деньги вовсе
2) Определить, какой из двух перечисленных вариантов будет выбран государством-кредитором X?
3) Изменилась ли его выгода от предоставленного кредита относительно исходных условий договора и в какую сторону?
Решение:
Будем рассматривать ситуацию с точки зрения страны-кредитора Х. Тогда предоставляемый кредит будет иметь отрицательный знак (деньги уходят из страны), а все остальные платежи будут положительными (деньги приходят в страну).
Приведем уравнение эквивалентности к начальному моменту времени. Получим балансовое уравнение:
Подставляем исходные параметры и находим неизвестный платеж:
Откуда получаем:
Рассмотрим вариант 1 реструктуризации второго платежа. Рассчитаем чистую приведенную сумму:
Так как баланс, составленный с точки зрения страны кредитора Х, оказался отрицательным, то можно сделать вывод, что данное изменение стране Х не выгодно, стране Х не стоит соглашаться на данное предложение.
Рассмотрим вариант 2 реструктуризации второго платежа. Рассчитаем чистую приведенную сумму:
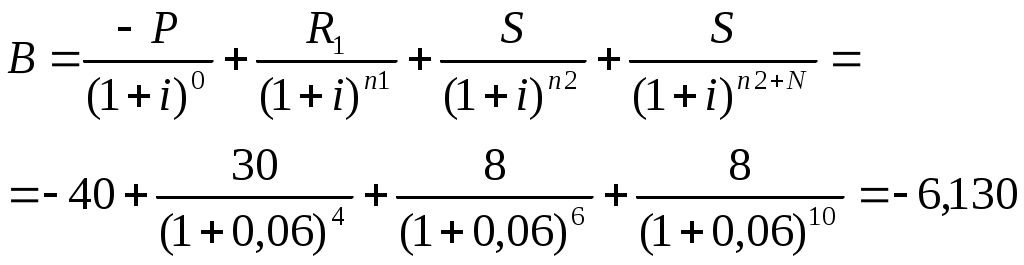
Так как баланс, составленный с точки зрения страны кредитора Х, оказался отрицательным, то можно сделать вывод, что данное изменение стране Х не выгодно, стране Х не стоит соглашаться на данное предложение.
Оба варианта стране Х не выгодно. Из двух невыгодных вариантов стране Х стоит выбрать второй вариант, т.к. потери будут меньше (-6,130 > -6,186). Для страны-заемщика Y оба варианты выгодны.
Вывод:
1) Сумма второго платежа по договору займа должна быть равна 23,033 млрд. €.
2) Государством-кредитором будет выбран 2-й вариант реструктуризации, потому что чистая приведенная стоимость по 1-му варианту (-6,186 млрд. €.) меньше, чем по 2-му варианту (-6,130 млрд. €.). Оба варианта реструктуризации не выгодны государству кредитору.
3) Первый вариант реструктуризации выгоднее для государства-заемщика, потому что чистая приведенная стоимость по 1-му варианту (-6,186 млрд. €.) меньше, чем по 2-му варианту (-6,130 млрд. €.).