Файл: Контрольная работа состоит из решения 10 практических заданий.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 177
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 2
Денежные средства в размере P = 850 000 рублей размещаются в виде рублевого депозита на один год с ежемесячным начислением процентов с капитализацией. Номинальная годовая ставка начисления процентов равна i = 10,0%.
Дата начала операции – 24 января 2021 года.
Операция прерывается раньше срока. Дата прерывания операции – 15 июля 2021 года.
Определить начисляемые проценты и наращенные суммы, если согласно договору при досрочном расторжении должна быть применена схема:
1) дробного процента;
2) смешанного процента;
3) без начисления процентов за неполный последний период начисления.
При расчетах неполного месяца считать, что в полном месяце 30 дней.
Решение:
Наращение по смешанному методу производится по формуле:
PV – сумма вложенных средств;
FV – наращенная сумма;
i – процентная ставка, отнесенная к расчетному периоду времени (год, квар-
тал, месяц и т.п.);
n N r – продолжительность времени между началом и концом финансовой операции;
N – число целых расчетных периодов между началом и концом операции;
r – оставшийся неполный интервал времени между началом и концом операции, выраженный в долях расчетного периода, всегда 0 r 1.
Определим полное число месяцев между датами финансовой операции. С 24 января по 15 июля пройдет 5 полных месяцев.
Найдем число дней между 24 июня и 15 июля. Между этими датами 21 день. Значит
Заметим, что начисления процентов происходят ежемесячно, а в договоре зафиксирована годовая процентная ставка j 10,0%0,1. Тогда ставка, отнесенная к расчетному периоду времени (месяцу) будет равна
Наращенная сумма по формуле смешанного процента будет равна:
(руб.)
Расчет суммы начисленных процентов:
Наращение по схеме без начисления процентов за неполный последний период начисления. При этой схеме наращение за все полные периоды проводится по схеме сложных процентов, а за оставшийся неполный период проценты не начисляются.
Расчет наращенной суммы:
Расчет суммы начисленных процентов:
Наращение по схеме с дробным периодом начисления. При этой схеме наращение за все периоды проводится по схеме сложных процентов, то есть в формуле сложного процента появляется дробный показатель степени.
Расчет суммы начисленных процентов:
Таблица 2
Основные результаты решения Задания 2
| Схема | Проценты, руб. | Наращенная сумма, руб. |
| Дробная | 41 180,29 | 891 180,29 |
| Смешанная | 36 011,88 | 886 011,88 |
| Без процентов за последний период | 41 173,85 | 891 173,85 |
Задание 3
У банка имеется возможность кратковременного размещения средств по двум схемам:
СХЕМА 1 – выдать денежные средства в размере P1 = 18 000 000 рублей на M1 = 5месяца и получить в конце операции Q1 = 28 100 000 рублей;
СХЕМА 2 – выдать денежные средства в размере P2= 10 600 000 рублей на M2 = 7 месяцев и получить в конце операции Q2 = 19 200 000 рублей.
Определить, какая из схем наиболее выгодна для банка, если операции оцениваются по правилу простого процента. Вывод обосновать.
Решение:
Сравнение краткосрочных финансовых операций проводится на основе сравнения эффективной процентной ставки для схемы простого процента.
Для схемы 1:
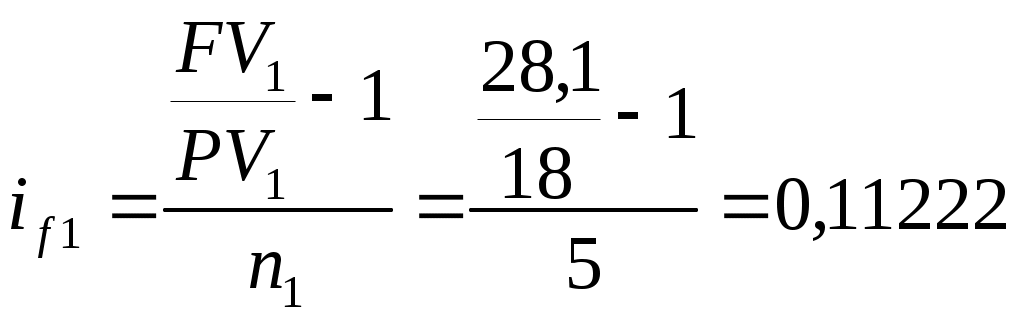 или 11,222%
или 11,222%Для схемы 2:
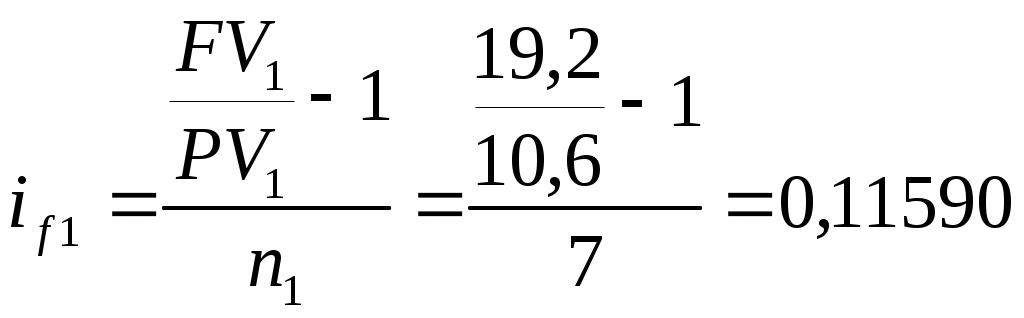 или 11,590%
или 11,590%Таким образом, эффективная ставка первой операции 11,222 % в месяц, а второй 11,59% в месяц. Для заемщика операция тем выгоднее, чем ниже процент, для банка, выдающего кредит – наоборот. Значит для банка выгоднее 2 вариант операции.
Задание 4
В банк сделан вклад в размере P = 850 000 рублей сроком на n = 10 лет под i= 10,0% годовых. Проценты начисляются по схеме сложного процента.
Определить, какая сумма будет возвращена в конце срока операции, если проценты начисляются и капитализируются:
а) раз в год;
б) раз в полгода;
в) раз в квартал;
г) раз в два месяца;
д) раз в месяц;
е) два раза в месяц;
ж) раз в неделю (считать, что в году ровно 53 недели);
з) раз в день (считать, что в году 365 дней);
и) непрерывно.
Для всех указанных случаев определить эффективную годовую процентную ставку (в этом задании – с точностью до тысячной доли процента).
Построить график зависимости эффективной процентной ставки от числа начислений процентов в год.
Решение:
а) раз в год
Проценты начисляются и капитализируются раз в год
, тогда m = 1
Наращенная сумма:
Эффективная ставка:
б) раз в полгода
Число периодов начислений в год: m = 2
Наращенная сумма:
Эффективная ставка:
в) раз в квартал
Число периодов начислений в год: m = 4
Наращенная сумма:
Эффективная ставка:
г) раз в два месяца
Число периодов начислений в год: m = 12 / 2 = 6
Наращенная сумма:
Эффективная ставка:
д) раз в месяц
Число периодов начислений в год: m = 12
Наращенная сумма:
Эффективная ставка:
е) два раза в месяц
Число периодов начислений в год: m = 24
Наращенная сумма:
Эффективная ставка:
ж) раз в неделю (считать, что в году ровно 53 недели)
Число периодов начислений в год: m = 53
Наращенная сумма:
Эффективная ставка:
з) раз в день (считать, что в году 365 дней)
Число периодов начислений в год: m = 365
Наращенная сумма:
Эффективная ставка:
и) непрерывно
Наращенная сумма:
Эффективная ставка:
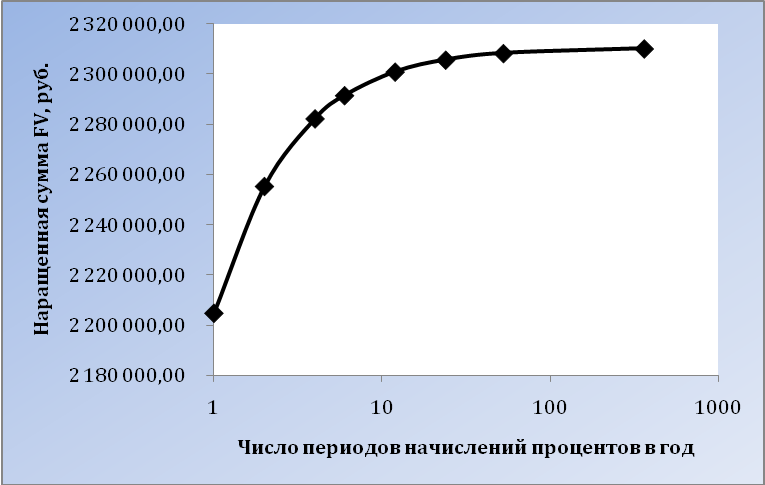
Рисунок 1 – График зависимости наращенной суммы от числа периодов начислений в год (логарифмическая шкала)
Как видно из графика, существенные изменения наращенной суммы происходят примерно до ежемесячных начислений (m12). При более частых начислениях наращенная сумма возрастает уже слабо.
Таблица 3
Основные результаты решения Задания 4
| Период начислений | Количество наращений в год | Наращенная сумма, руб. | Эффективная ставка, % |
| раз в год | 1 | 2 204 681,09 | 10,000 |
| раз в пол года | 2 | 2 255 303,05 | 10,250 |
| раз в квартал | 4 | 2 282 304,26 | 10,381 |
| раз в 2 месяца | 6 | 2 291 574,62 | 10,426 |
| раз в месяц | 12 | 2 300 985,27 | 10,471 |
| 2 раза в месяц | 24 | 2 305 744,24 | 10,494 |
| раз в неделю | 53 | 2 308 363,56 | 10,507 |
| раз в день | 365 | 2 310 223,12 | 10,516 |
| непрерывно | бесконечно | 2 310 424,04 | 10,517 |