Файл: Контрольная работа состоит из решения 10 практических заданий.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 178
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 9
Инвестор рассматривает вариант покупки торгового комплекса за P0 = 165 млн. руб. Перестройка комплекса потребует вложения через год еще P1 = 100 млн.руб. Оборудование комплекса обойдется в P2 = 53 млн. руб. и эти затраты будутпроизведены через 2 года.
Прибыль от комплекса ожидается в размере D1 = 152 млн. руб. через n1 = 4 года, D2 = 260 млн. руб. через n2 = 6 лет и D3 = 330 млн. руб. через n3 = 7 лет.
В конце n4 = 10 года комплекс планируется продать за S = 390 млн. руб. В остальные годы доходы и расходы практически компенсируют друг друга.
1. Определить (только на основе понятия чистого приведенного дохода NPV):
а) выгоден ли для инвестора предлагаемый проект, если он ожидает от вложения нормы доходности не ниже чем i = 16% годовых?
б) останется ли проект выгодным, если ожидания инвестора станут равными i 2036% годовых?
2. Определить с использованием функции ВСД MS Excel внутреннюю
норму доходности (IRR) проекта. Ответить на пункты (а) и (б) вопроса 1 на
основе понятия внутренней норы доходности.
3. Определить срок окупаемости проекта для случая (а), понимая под данным понятием год, когда проект даст первый положительный накопленный чистый приведенный доход.
Решение:
1. Рассчитаем чистый приведенный доход при ставке 10,0%:
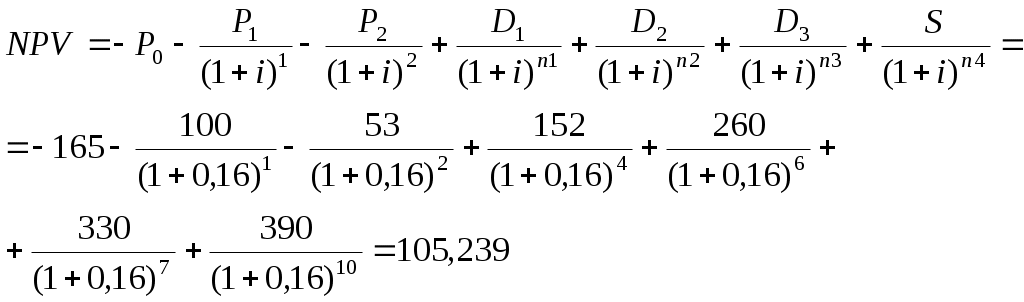
Т.к. NPV = 105,239 млн. руб. > 0, то проект считается выгодным при ставке дисконтирования i= 16%.
2. Рассчитаем чистый приведенный доход при ставке 36%:
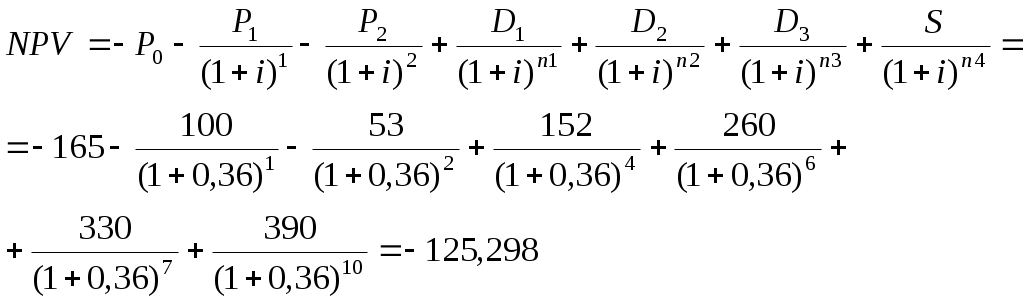
Т.к. NPV = -125,298 млн. руб. < 0, то проект считается не выгодным при ставке дисконтирования
i= 36%.
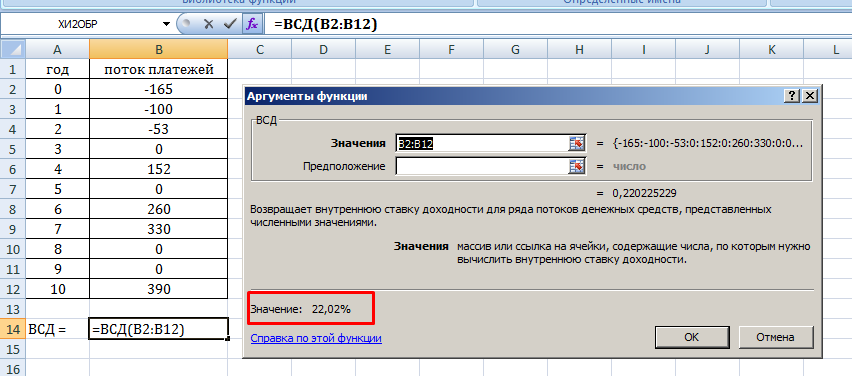
Рисунок 2 – Использование функции ВСД
3. Определим внутреннюю норму доходности (IRR)
Сформируем на чистом листе Excel потоки платежей (в 3-й, 5-й, 8-й и 9-й годы потоков не было, поэтому ставим 0).
Внутренняя норма доходности определяет такую ставку, при которой чистый приведенных доход будет равен нулю:
NPV = 0
Далее используем функцию ВСД (рисунок 2).
Получаем IRR = 0,2202 или 22,02%
Если инвестор рассчитывает на доходность 16%, то проект выгоден (22,02% 16%). Если инвестор рассчитывает на доходность 36%, то проект невыгоден (так как 22,02 % 36%). При ставке 22,02% проект не будет прибылен или убыточен, чистый приведенных доход по нему будет равен нулю.
4. Определим срок окупаемости проекта для случая когда i = 16%
1) На начальном этапе (нулевой период времени) имеем вложения 165 млн. руб.
2) В 1-й год имеем вложения 100 млн. руб. Накопленная чистая приведенная стоимость составит:
3) Во 2-й год имеем вложения 53 млн. руб. Накопленная чистая приведенная стоимость составит:
4) В 4-й год имели прибыль в 152 млн. руб. Накопленная чистая приведенная стоимость составит:
5) В 6-й год имели прибыль в 260 млн. руб. Накопленная чистая приведенная стоимость составит:
6) В 7-й год имели прибыль в 330 млн. руб. Накопленная чистая приведенная стоимость составит:
Таким образом, на 6 шаге расчетов мы получили положительное значение накопленного NPV . Значит, период окупаемости равен n = 7 лет.
Задание 10
Банк предлагает предпринимателю кредит в размере P = 850 000 рублей с номинальной годовой процентной ставкой i = 10,0%. Проценты начисляются ежемесячно. Срок кредита n = 3 года, интервалы выплат – раз в квартал.
Есть два возможных способа возврата кредита:
«аннуитет» – общие выплаты равными платежами;
«дифференцированный» – равными выплатами основной части долга.
1. Составить таблицы выплат по обоим вариантам. Выделить выплаты
основной части долга и выплаты процентов. Определить суммарные значения указанных величин.
2. По полученной таблице построить на одной диаграмме шесть графиков зависимостей по датам:
общих выплат по обоим вариантам;
выплат основной части по обоим вариантам;
выплат процентов для обоих вариантов.
3. На основе таблицы п. 1. составить таблицу дисконтированных на момент взятия кредита суммарных выплат по обоим вариантам для трех номинальных ставок дисконтирования:
а) ставки кредита i = 10%;
б) ставки i 4= 10 - 4 = 6%
в) ставки i = 10 + 4 = 14%
При дисконтировании учитывать ежемесячное начисление процентов.
Определить суммы дисконтированных величин.
4. Сделать вывод о выгодности для предпринимателя той или иной схемы получения кредита в зависимости от нормы прибыли в его бизнесе.
5. Какие еще выводы можно сделать на основе решения этого задания?
m – число периодов начислений процентов в год. Проценты начисляются ежемесячно (m = 12);
q – число интервалов выплат за год. Выплаты производятся раз в квартал, т.е. 4 раза в год (q = 4).
Расчет размера платежа:
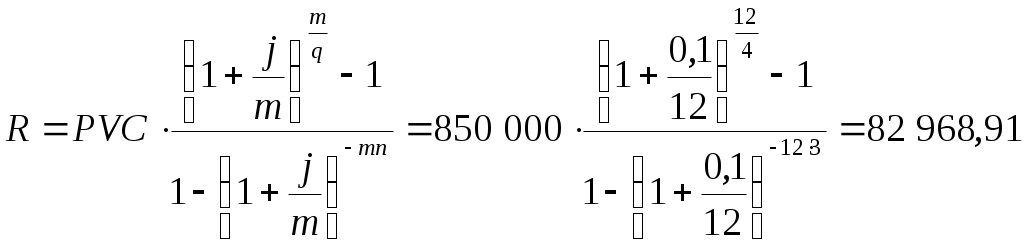
Таблица 6
План погашения долга аннуитетными платежами
| Год | квартал | Долг на начало периода, руб. | Долг на конец периода, руб. | Сумма начисленных процентов, руб. | Размер равного платежа, руб. | Долг на конец периода после выплаты, руб. |
| 1 | 1 | 850 000,00 | 871 427,58 | 21 427,58 | 82 968,91 | 788 458,67 |
| 2 | 788 458,67 | 808 334,85 | 19 876,19 | 82 968,91 | 725 365,94 | |
| 3 | 725 365,94 | 743 651,63 | 18 285,69 | 82 968,91 | 660 682,72 | |
| 4 | 660 682,72 | 677 337,81 | 16 655,09 | 82 968,91 | 594 368,90 | |
| 2 | 1 | 594 368,90 | 609 352,29 | 14 983,39 | 82 968,91 | 526 383,38 |
| 2 | 526 383,38 | 539 652,94 | 13 269,55 | 82 968,91 | 456 684,03 | |
| 3 | 456 684,03 | 468 196,53 | 11 512,51 | 82 968,91 | 385 227,62 | |
| 4 | 385 227,62 | 394 938,79 | 9 711,17 | 82 968,91 | 311 969,88 | |
| 3 | 1 | 311 969,88 | 319 834,31 | 7 864,42 | 82 968,91 | 236 865,40 |
| 2 | 236 865,40 | 242 836,51 | 5 971,12 | 82 968,91 | 159 867,60 | |
| 3 | 159 867,60 | 163 897,69 | 4 030,09 | 82 968,91 | 80 928,78 | |
| 4 | 80 928,78 | 82 968,91 | 2 040,13 | 82 968,91 | 0,00 | |
| Σ | | | | 145 626,92 | 995 626,92 | |
Так как всего будет 12 выплат, то простая бухгалтерская сумма выплат будет равна:
12×82 968,91 = 995 626,92 руб.
Очевидно, простая бухгалтерская переплата может быть определена как разность между бухгалтерской суммой и исходной суммой кредита. По-
лучим:
995 626,92 – 850 000 = 145 626,92 руб.
То есть всего предприниматель заплатит 995 626,92 руб., переплатив по сравнению с исходной суммой 145 626,92 руб. (все это без учета изменения ценности денег с течением времени).
Определим выплаты процентов и основной части долга. Они будут различны для разных периодов выплат. Детализация расчетов по аннуитету представлена в таблице 6.
2. Рассчитаем параметры для дифференцированного кредита
В этом случае кредит погашается так, чтобы основной долг выплачивался равными платежами:
Определим ежепериодические выплаты процентов и общие выплаты. Они будут различны для разных периодов выплат.
Расчет представлен в таблице 7.
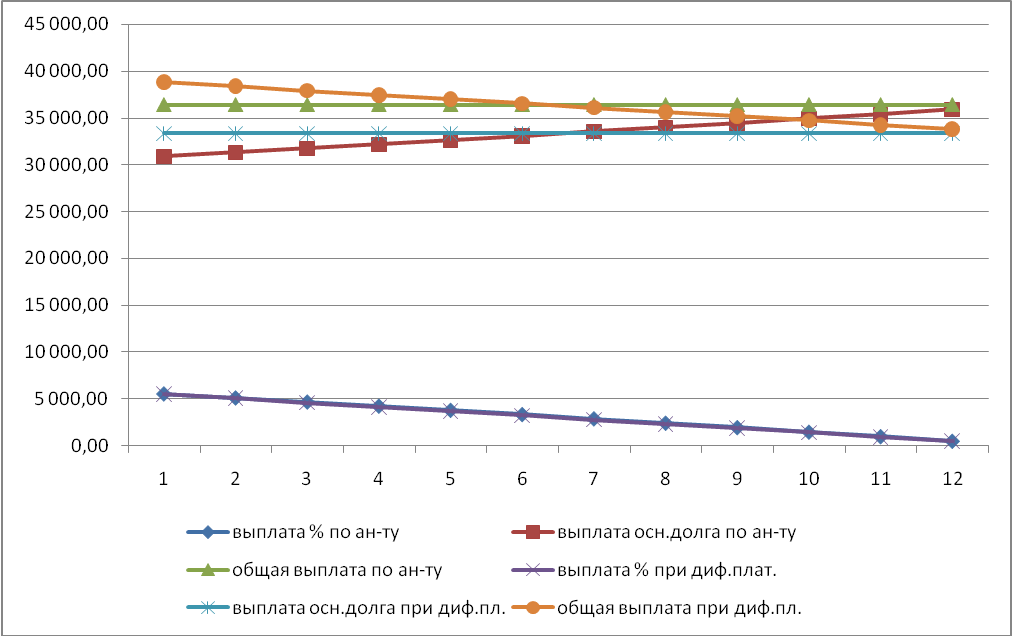
Рисунок 3 – Графики погашения долга
Таблица 7
План погашения долга по дифференцированным платежам
| Год | квартал | Долг на начало периода, руб. | Долг на конец периода, руб. | Сумма начисленных процентов, руб. | Размер платежа оп основному долгу, руб. | Общий размер платежа (проценты + по основному долгу), руб. | Долг на конец периода после выплаты, руб. |
| 1 | 1 | 850 000,00 | 871 427,58 | 21 427,58 | 70 833,33 | 92 260,91 | 779 166,67 |
| 2 | 779 166,67 | 798 808,61 | 19 641,94 | 70 833,33 | 90 475,28 | 708 333,33 | |
| 3 | 708 333,33 | 726 189,65 | 17 856,31 | 70 833,33 | 88 689,65 | 637 500,00 | |
| 4 | 637 500,00 | 653 570,68 | 16 070,68 | 70 833,33 | 86 904,01 | 566 666,67 | |
| 2 | 1 | 566 666,67 | 580 951,72 | 14 285,05 | 70 833,33 | 85 118,38 | 495 833,33 |
| 2 | 495 833,33 | 508 332,75 | 12 499,42 | 70 833,33 | 83 332,75 | 425 000,00 | |
| 3 | 425 000,00 | 435 713,79 | 10 713,79 | 70 833,33 | 81 547,12 | 354 166,67 | |
| 4 | 354 166,67 | 363 094,82 | 8 928,16 | 70 833,33 | 79 761,49 | 283 333,33 | |
| 3 | 1 | 283 333,33 | 290 475,86 | 7 142,53 | 70 833,33 | 77 975,86 | 212 500,00 |
| 2 | 212 500,00 | 217 856,89 | 5 356,89 | 70 833,33 | 76 190,23 | 141 666,67 | |
| 3 | 141 666,67 | 145 237,93 | 3 571,26 | 70 833,33 | 74 404,60 | 70 833,33 | |
| 4 | 70 833,33 | 72 618,96 | 1 785,63 | 70 833,33 | 72 618,96 | 0,00 | |
| Итого | | | | 139 279,24 | 850 000,00 | 989 279,24 | |
То есть всего предприниматель заплатит 989279,24 руб., переплатив по сравнению с исходной суммой 139 279,24 руб. (все это без учета изменения ценности денег с течением времени).
3. Дисконтирование
Дисконтирование осуществляется по формуле:
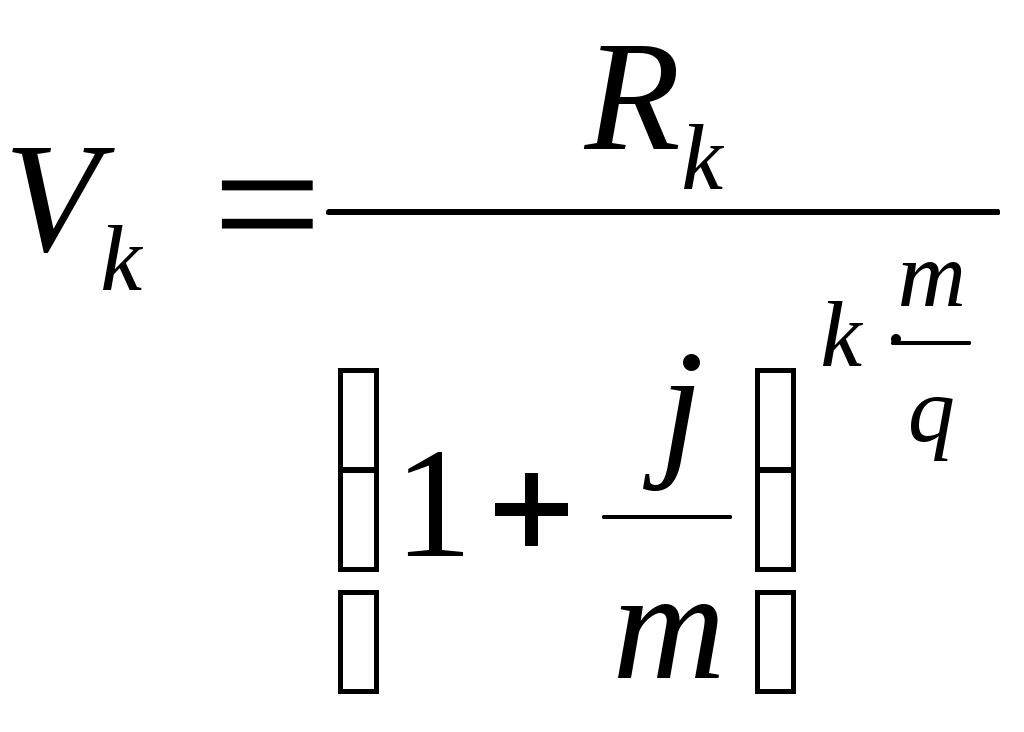
Для ставки 10% получим формулу:
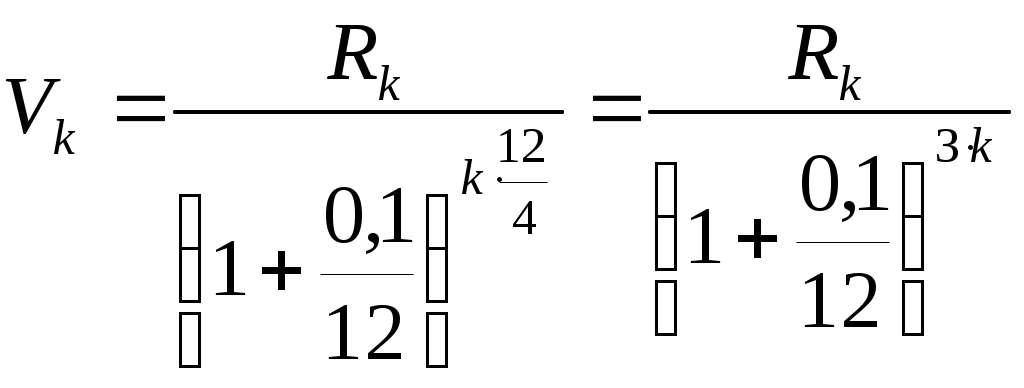
Таблица 8
Расчет дисконтированных выплат (по аннуитету и дифференцированных)
по ставке 10%
| Год | платеж | платежи | дисконтированные платежи | ||
| Аннуитетный | дифференцированный | Аннуитетный | дифференцированный | ||
| 1 | 1 | 82 968,91 | 92 260,91 | 80928,78 | 89992,30 |
| 2 | 82 968,91 | 90 475,28 | 78938,82 | 86080,58 | |
| 3 | 82 968,91 | 88 689,65 | 76997,79 | 82306,82 | |
| 4 | 82 968,91 | 86 904,01 | 75104,49 | 78666,59 | |
| 2 | 5 | 82 968,91 | 85 118,38 | 73257,74 | 75155,63 |
| 6 | 82 968,91 | 83 332,75 | 71456,40 | 71769,76 | |
| 7 | 82 968,91 | 81 547,12 | 69699,36 | 68504,96 | |
| 8 | 82 968,91 | 79 761,49 | 67985,52 | 65357,33 | |
| 3 | 9 | 82 968,91 | 77 975,86 | 66313,82 | 62323,07 |
| 10 | 82 968,91 | 76 190,23 | 64683,22 | 59398,51 | |
| 11 | 82 968,91 | 74 404,60 | 63092,72 | 56580,09 | |
| 12 | 82 968,91 | 72 618,96 | 61541,33 | 53864,37 | |
| Итого | | 995 626,92 | 989 279,24 | 850000,00 | 850000,00 |