Файл: Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc
Добавлен: 09.11.2023
Просмотров: 176
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Расположение корней квадратного трехчлена на числовой оси
Изучение этого вопроса закладывает базу для решения тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств с параметрами. Во многих случаях эти решения приводят к громоздким преобразованиям. В то же время использование свойств квадратичной функции позволяет существенно упростить решение.
Кроме того, решение многих задач с параметрами, предлагающихся на вступительных экзаменах в вузы, требует умения правильно формулировать необходимые и достаточные условия, связанные с расположением корней квадратного трехчлена относительно некоторых характерных точек.
Основное внимание уделено наглядности, обоснование утверждений существенно опирается на чертеж.
Пусть квадратный трехчлен f(x)=Ax2+Bx+Cимеет корни х1 и х2; х0=
Все чертежи приведены для а>0, случай а<0 рассматривается аналогично.
У
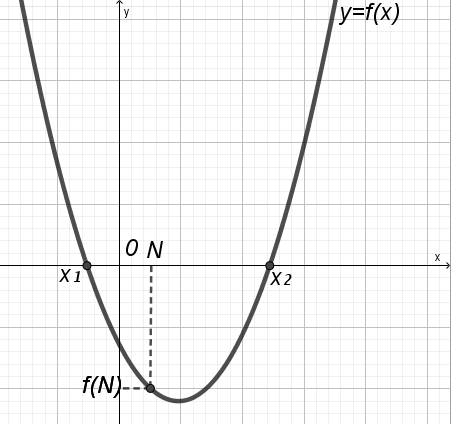 тверждение 1. Для того, чтобы число N было расположено между корнями квадратного трехчлена (х1<N<х2), необходимо и достаточно выполнение неравенства
тверждение 1. Для того, чтобы число N было расположено между корнями квадратного трехчлена (х1<N<х2), необходимо и достаточно выполнение неравенстваА f(N)<0
Доказательство:
Nx1>0; Nx2<0;
(N x1)( N x2)<0;
N2 x1N x2N+x1 x2<0;
N2 (x1+x2)N+x1 x2<0;
N2+
<0 xa2;
A (AN2+BN+C)<0;
af(N)<0.
88. При каких mуравнение x2 (2m+1)x+3m 4=0 имеет два корня, один из которых меньше 2, а другой больше 2?
Решение: А f(2)<0;
A=1; f(2)=4 (2m+1) 2+3m 4=m 2;
m 2<0; m>2.
Ответ: m>2.
89. При каких mуравнение mx2+(3m 2)x+m 3=0 имеет корни разных знаков?
Эту задачу можно переформулировать так: при каких m число 0 лежит между корнями уравнения?
Решение: А=m; f(0)=m 3;
m(m 3)<0; 0<m<3.
Ответ: (0; 3).
Замечание: Эту задачу можно решить и используя теорему Виета (
90. При каких kодин из корней уравнения (k2 2)x2+(k2+k 1)xk3+k2=0 меньше k, а другой больше k?
Решение: А=k2 2;
f(k)=(k2 2)k2+ (k2+ k 1)k k3+k2= (k2 2) ((k2 2)k2+ (k2+ k 1)k k3+k2)<0;

Ответ: (
У
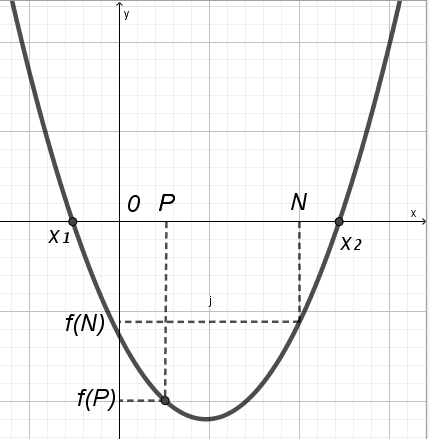 тверждение 2. Для того, чтобы отрезок [N; P] лежал в интервале (х1; х2), необходимо и достаточно выполнение условий:
тверждение 2. Для того, чтобы отрезок [N; P] лежал в интервале (х1; х2), необходимо и достаточно выполнение условий: 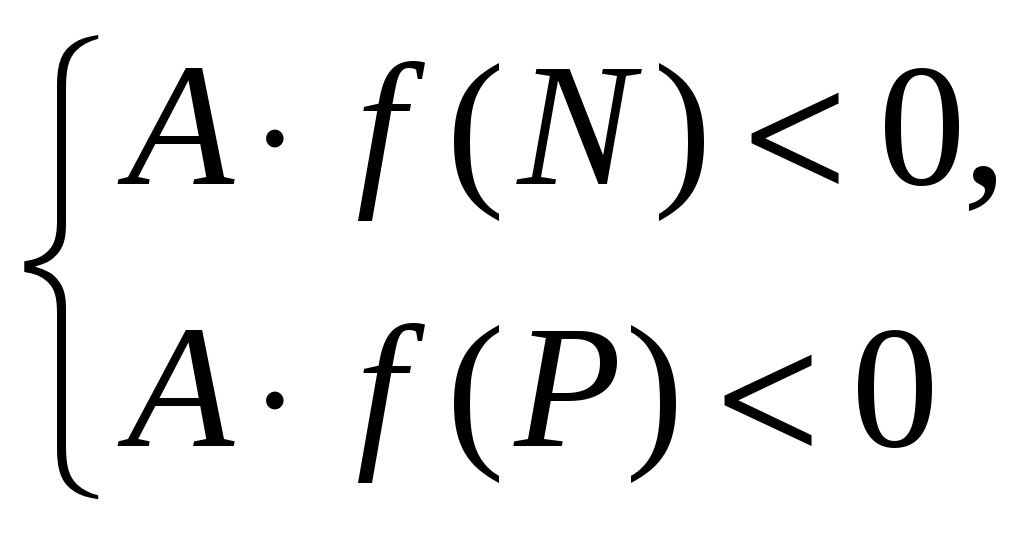
91. При каких mкорни уравнения
(m 1)x2 2(m+2)x+3m=0 удовлетворяют условию х1<2, х2>4?
Решение:
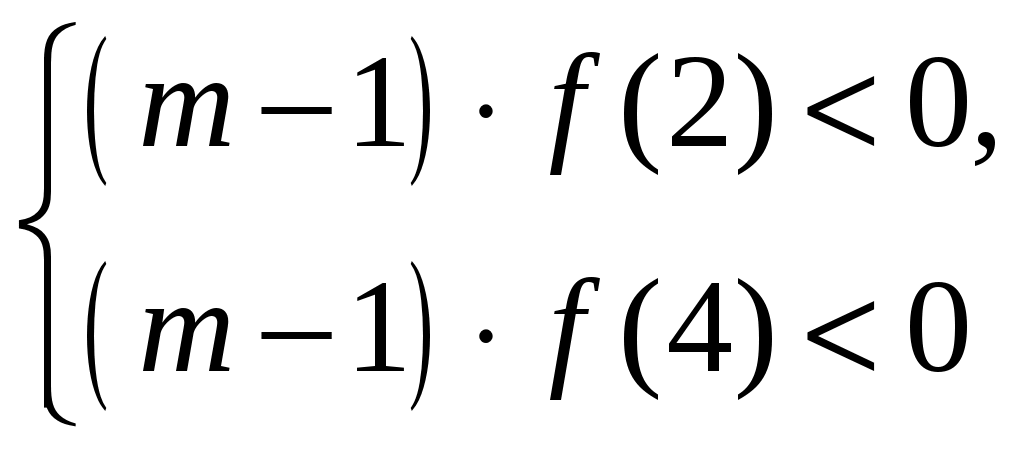
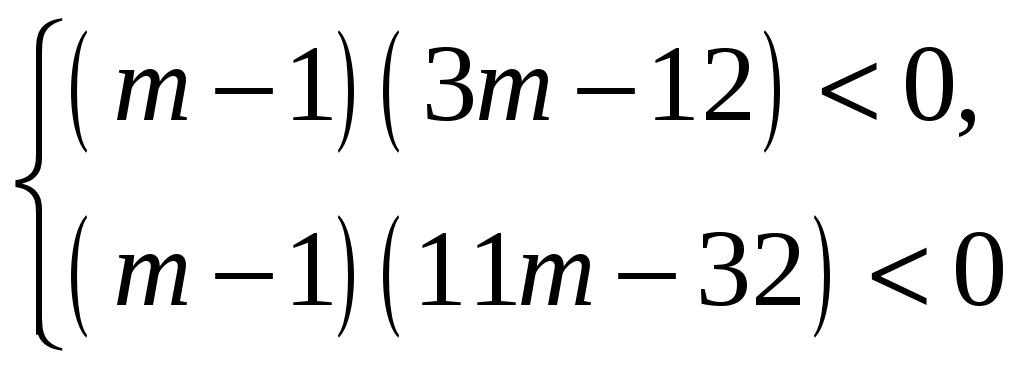
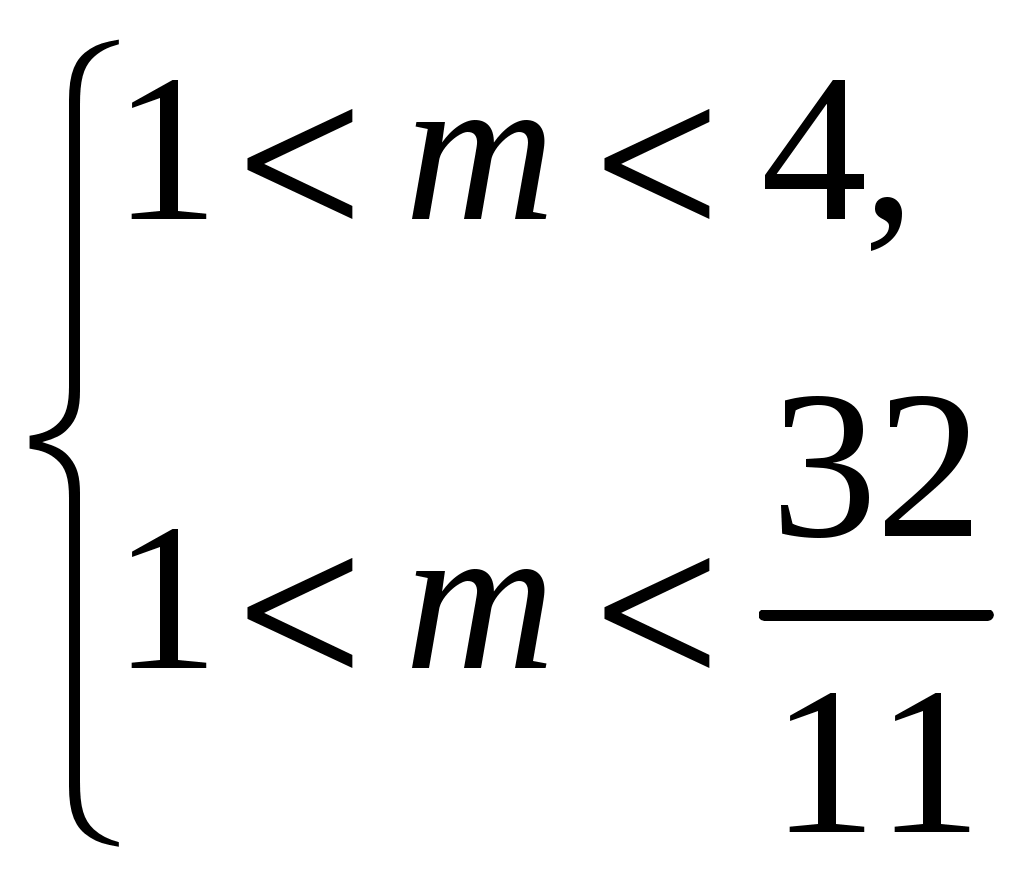

Ответ:
92. Найти все значения а, при которых неравенство x22(а3)x+а26а<0 будет выполнено для любого х, принадлежащего интервалу (0; 2).
Решение: Интервал (0; 2) должен содержаться во множестве решений данного неравенства, следовательно, должно выполняться соотношение
х1 0<2 х2
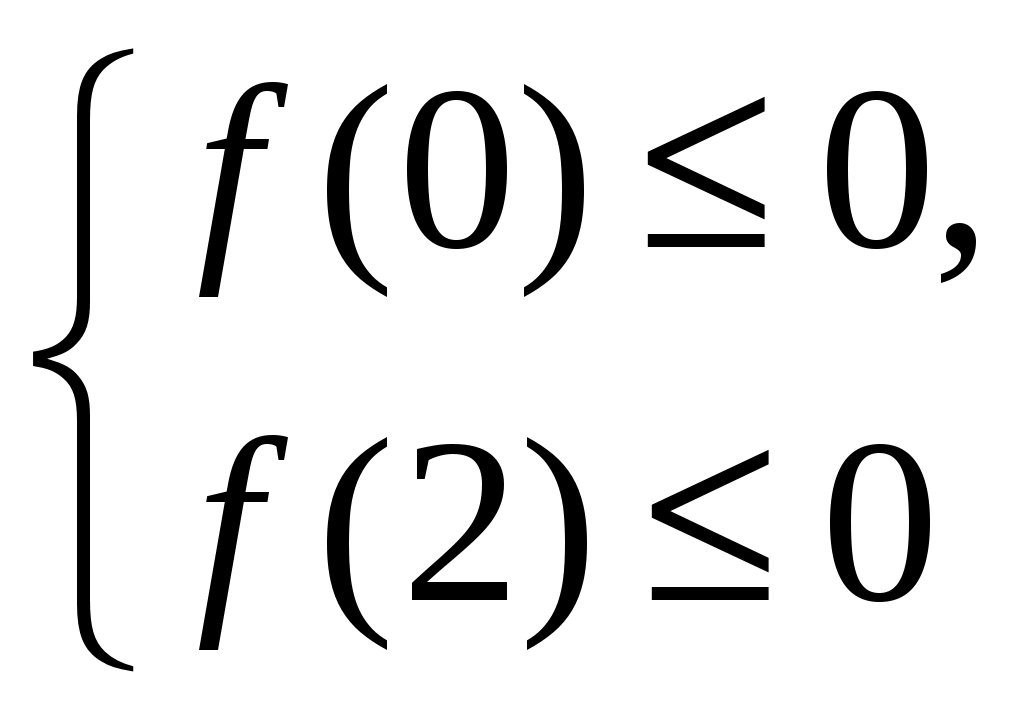
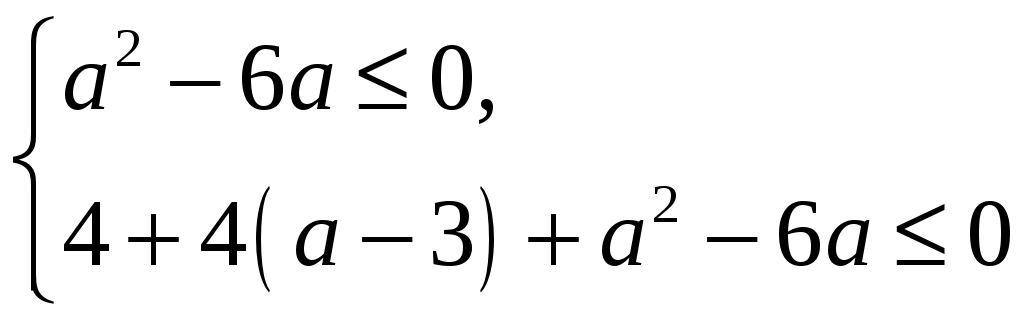
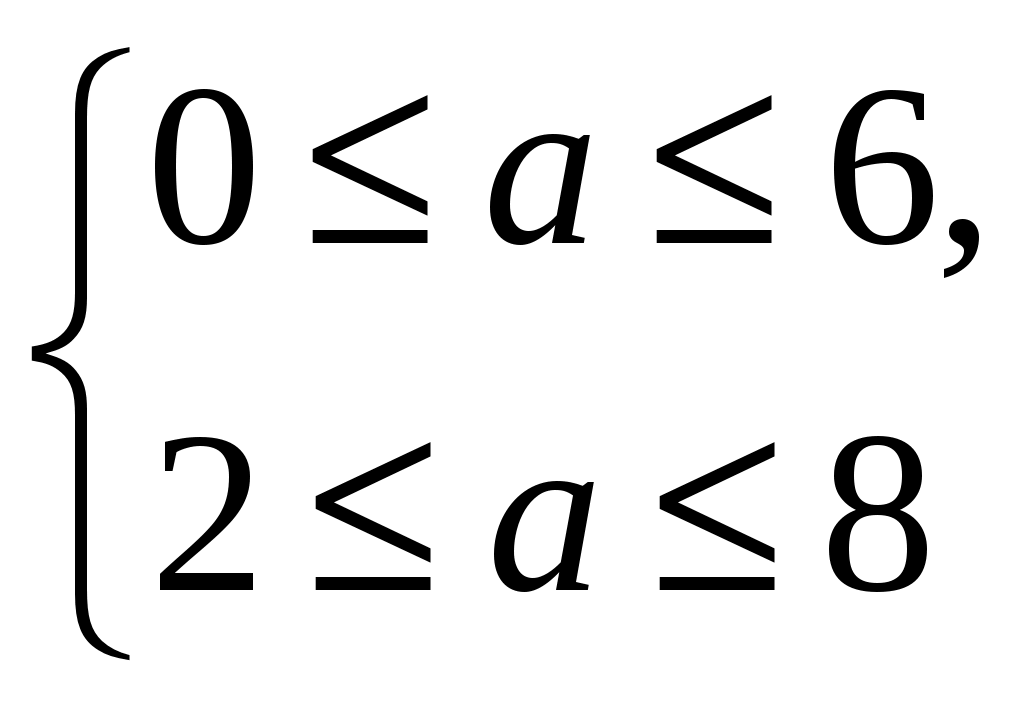
Ответ: [2;6 ].
Утверждение 3. Для того, чтобы оба корня квадратного трехчлена были меньше числа M (х1х2M), необходимо и достаточно выполнение условий:
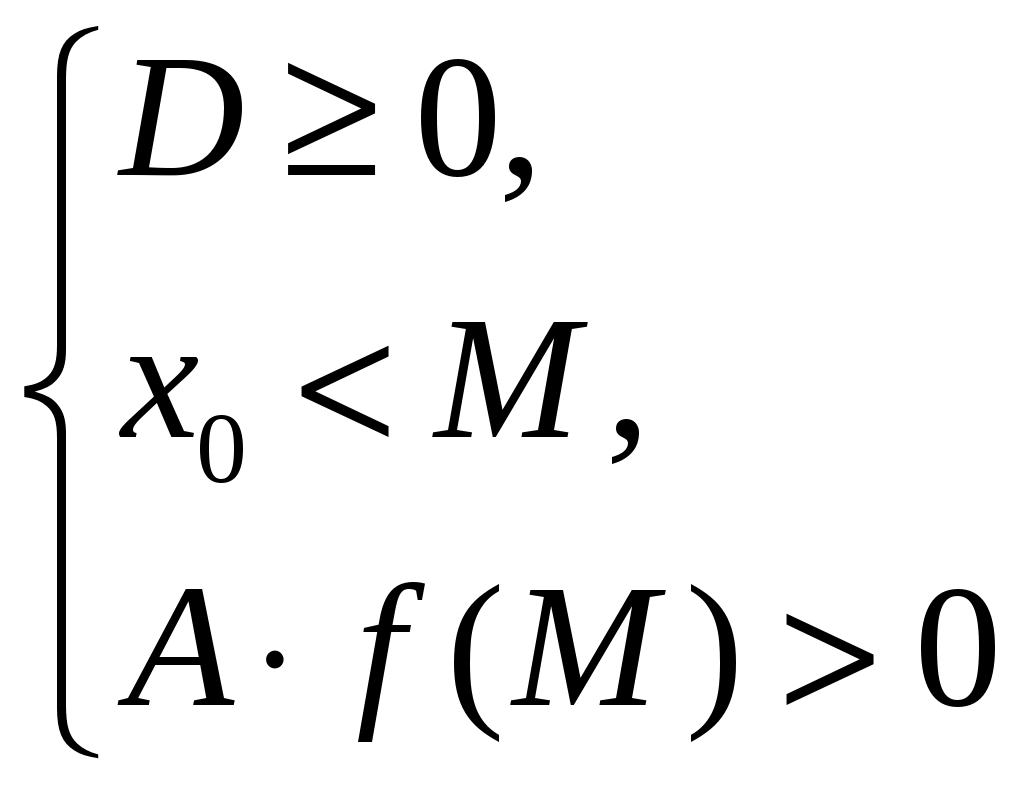

Доказательство.
(x1M)<0; (x2M)<0;
(x1M)(x2M)>0;
M2(x1+x2)M+x1 x2>0;
M2+
M+
a(aM2+BM+C) 0;
af(M)>0.
У
 тверждение 4. Для того, чтобы оба корня уравнения были больше числа K (K<х1х2), необходимо и достаточно выполнение условий:
тверждение 4. Для того, чтобы оба корня уравнения были больше числа K (K<х1х2), необходимо и достаточно выполнение условий: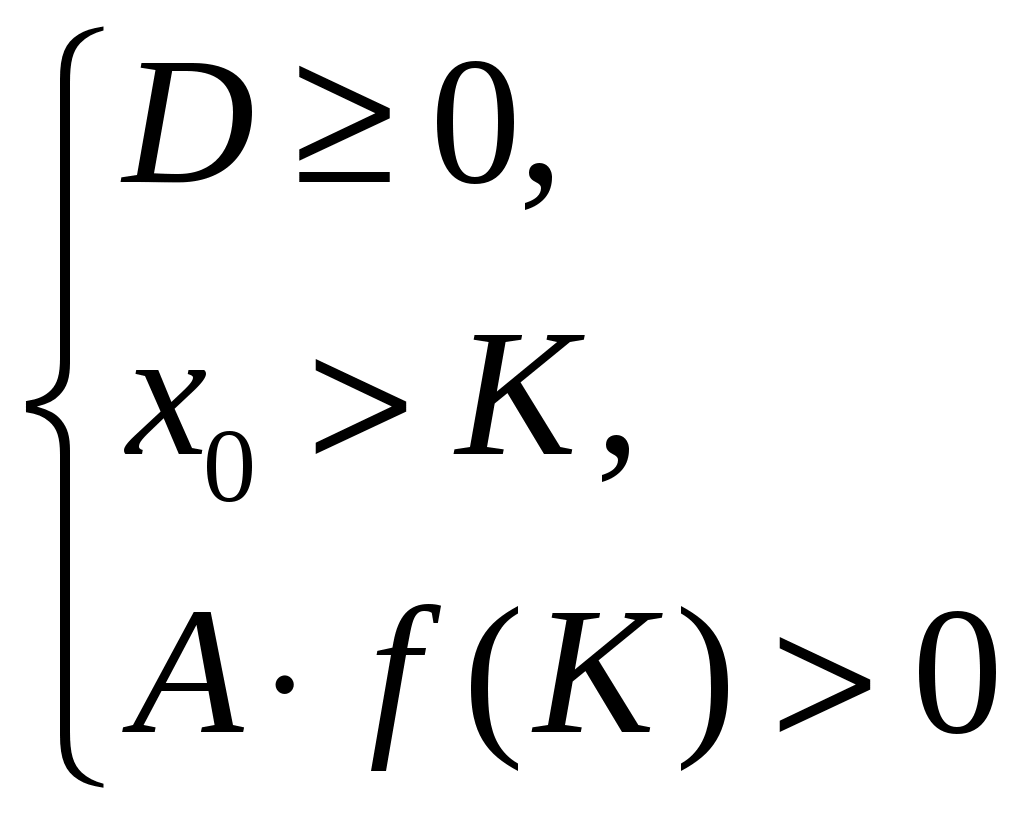
93. При каких mвсе корни уравнения x2 (3m+1)x+(2m2+4m 6)=0
а) больше 1; б) меньше 1?


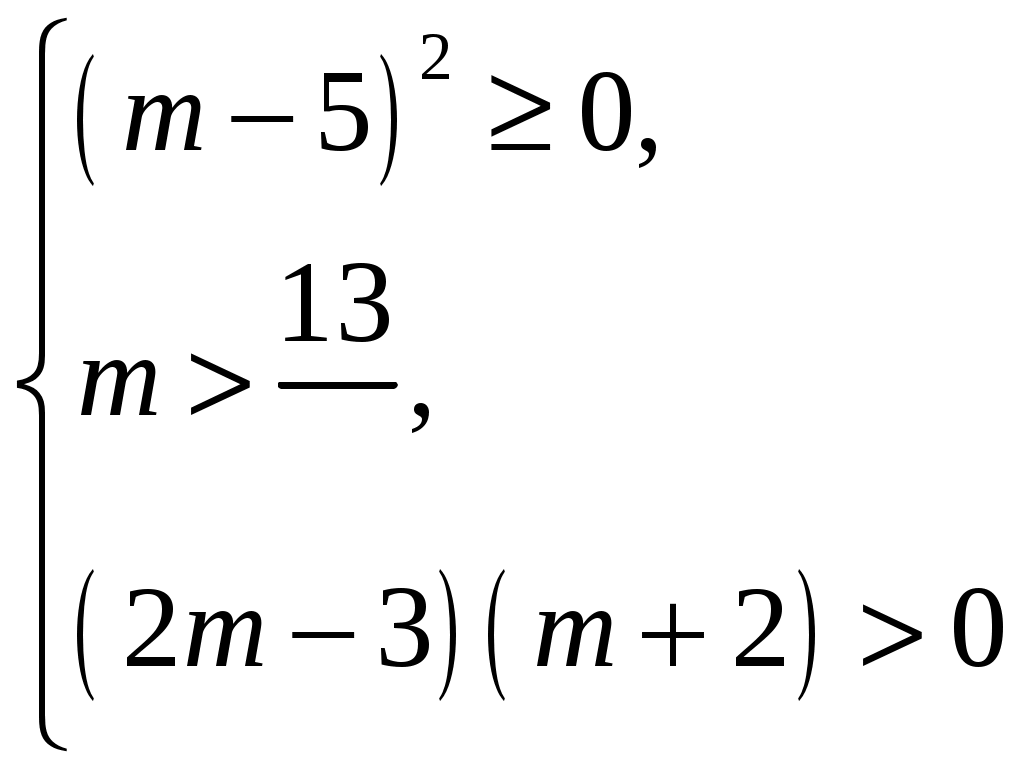
Решение: а)

б)
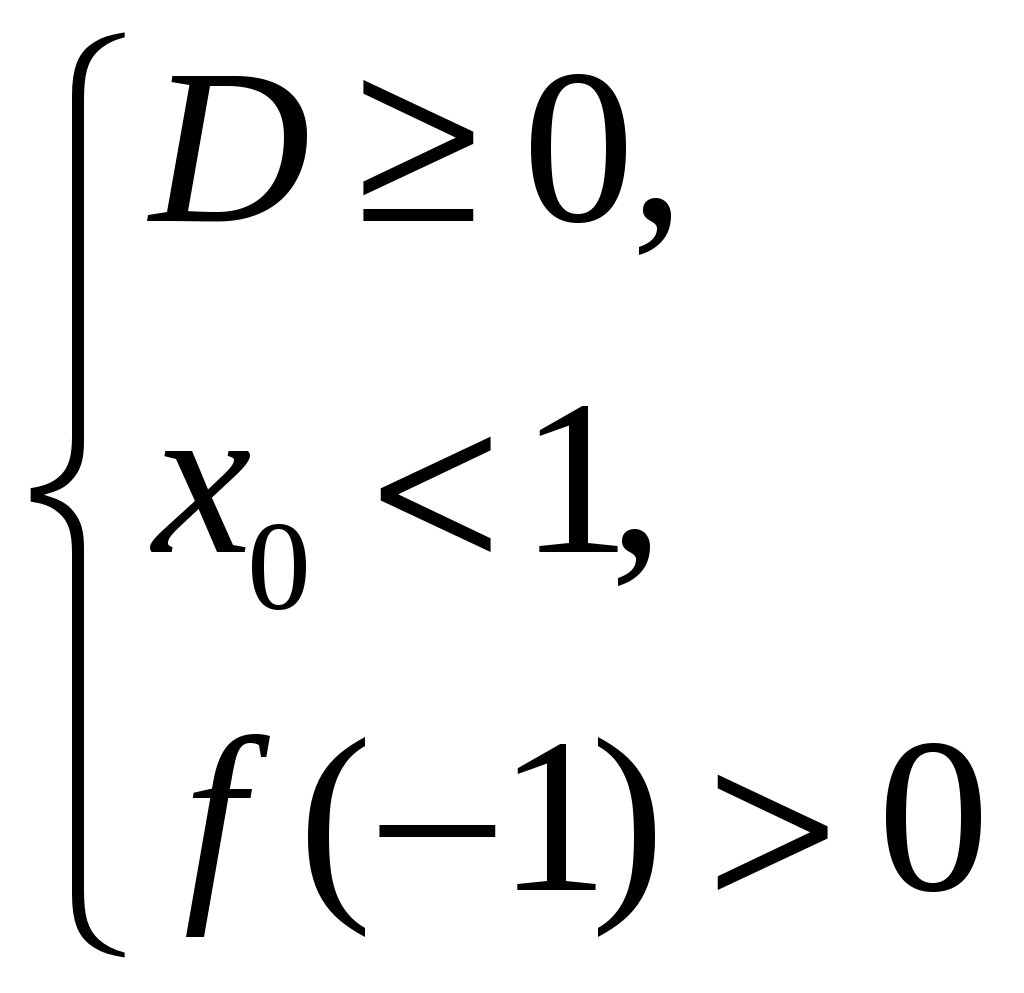

Ответ: а) m>
Замечание: Если выражения для корней уравнения не содержат радикалов, то удобно решать примеры и без применения теорем. Так как корни х1=m+3, x2=2m 2, то в случае
а)
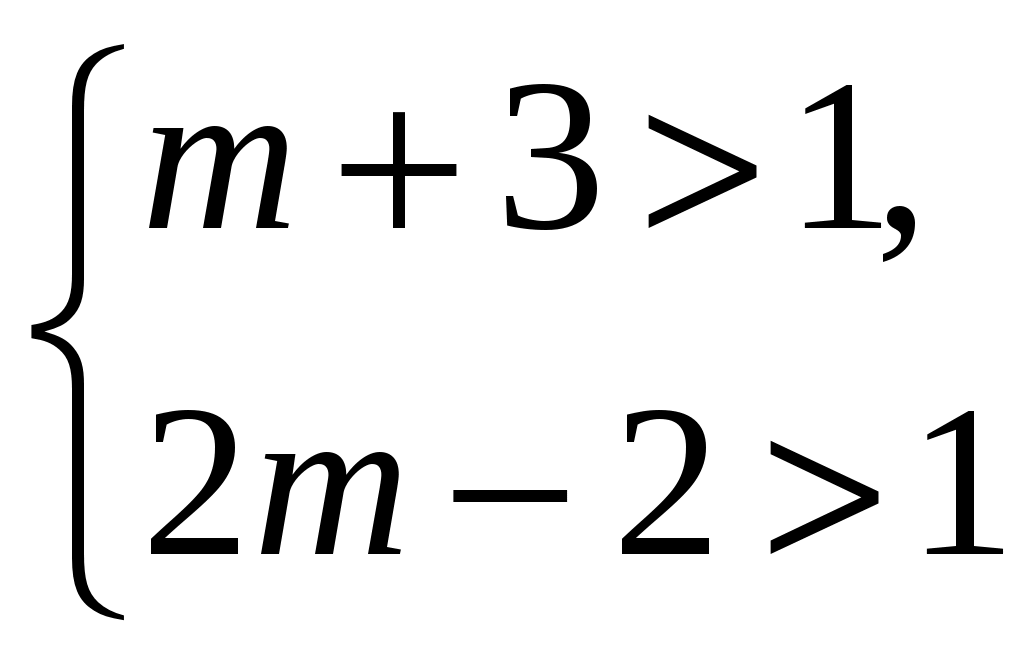

94. При каких а корни уравнения
аx2 (2а+1)x+3а 1=0 больше 1?
Ответ:
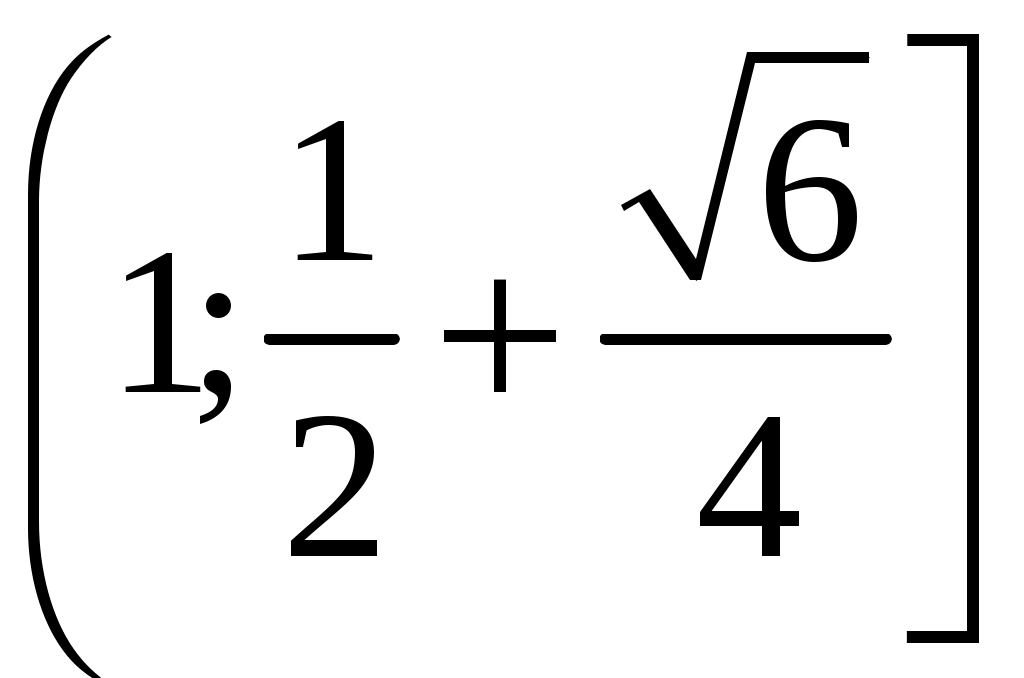 .
.9
 5. При каких р корни уравнения x2+4рх+(1 2р+4р2)=0 меньше 1?
5. При каких р корни уравнения x2+4рх+(1 2р+4р2)=0 меньше 1?Ответ: (1;+).
96. При каких bкорни уравнения x2 2xb=0 меньше b?
Ответ: (3;+).
Утверждение 5. Для того, чтобы оба корня квадратного трехчлена лежали в интервале (K; M), т. е. K<x1x2<M, необходимо и достаточно выполнение условий:
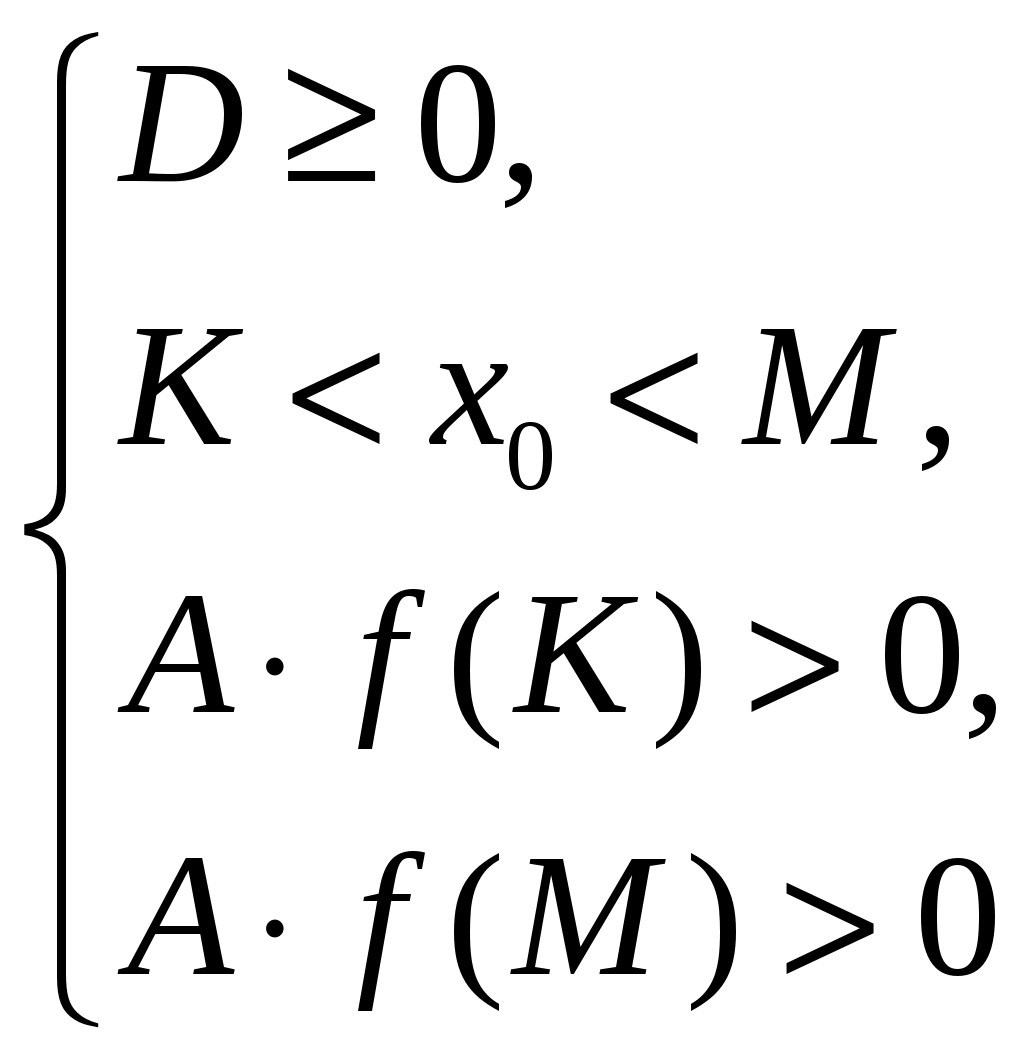
97. Для каких значений mуравнение 4x22x+m=0 имеет корни, заключенные между 1 и 1?
Решение:

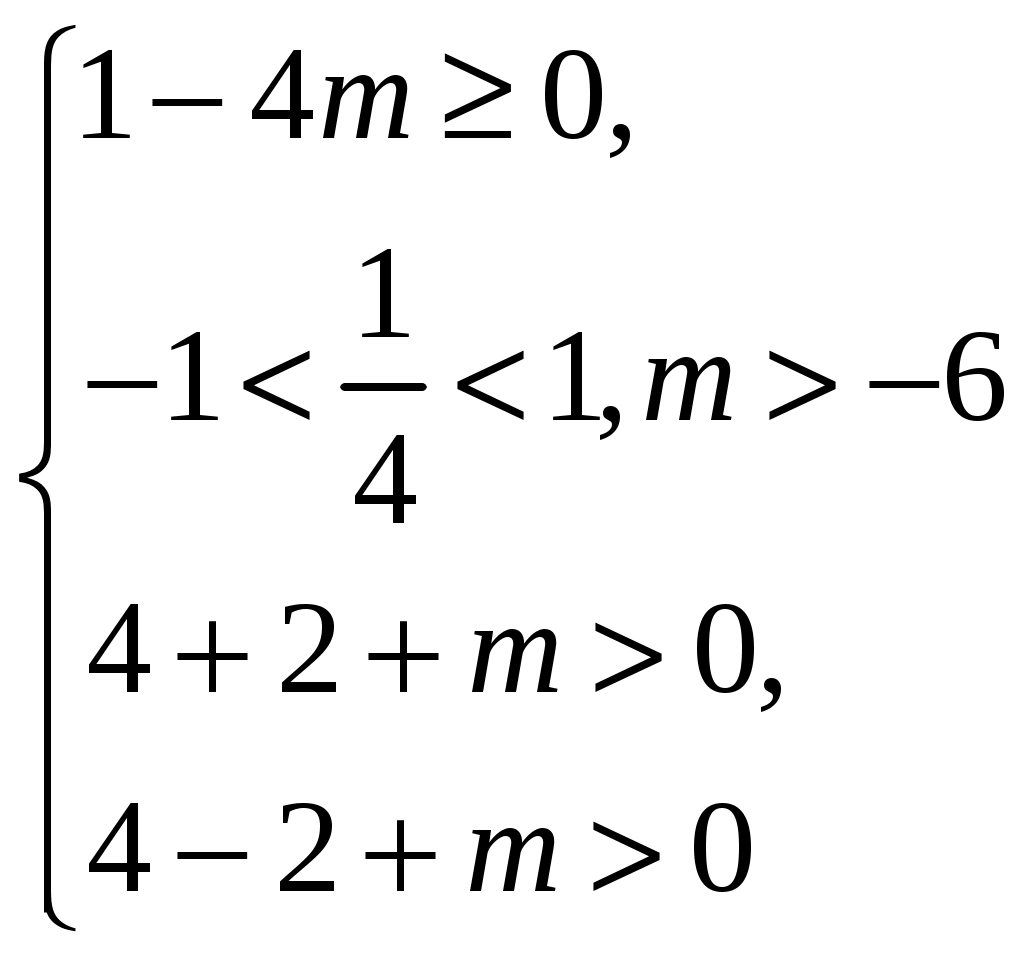
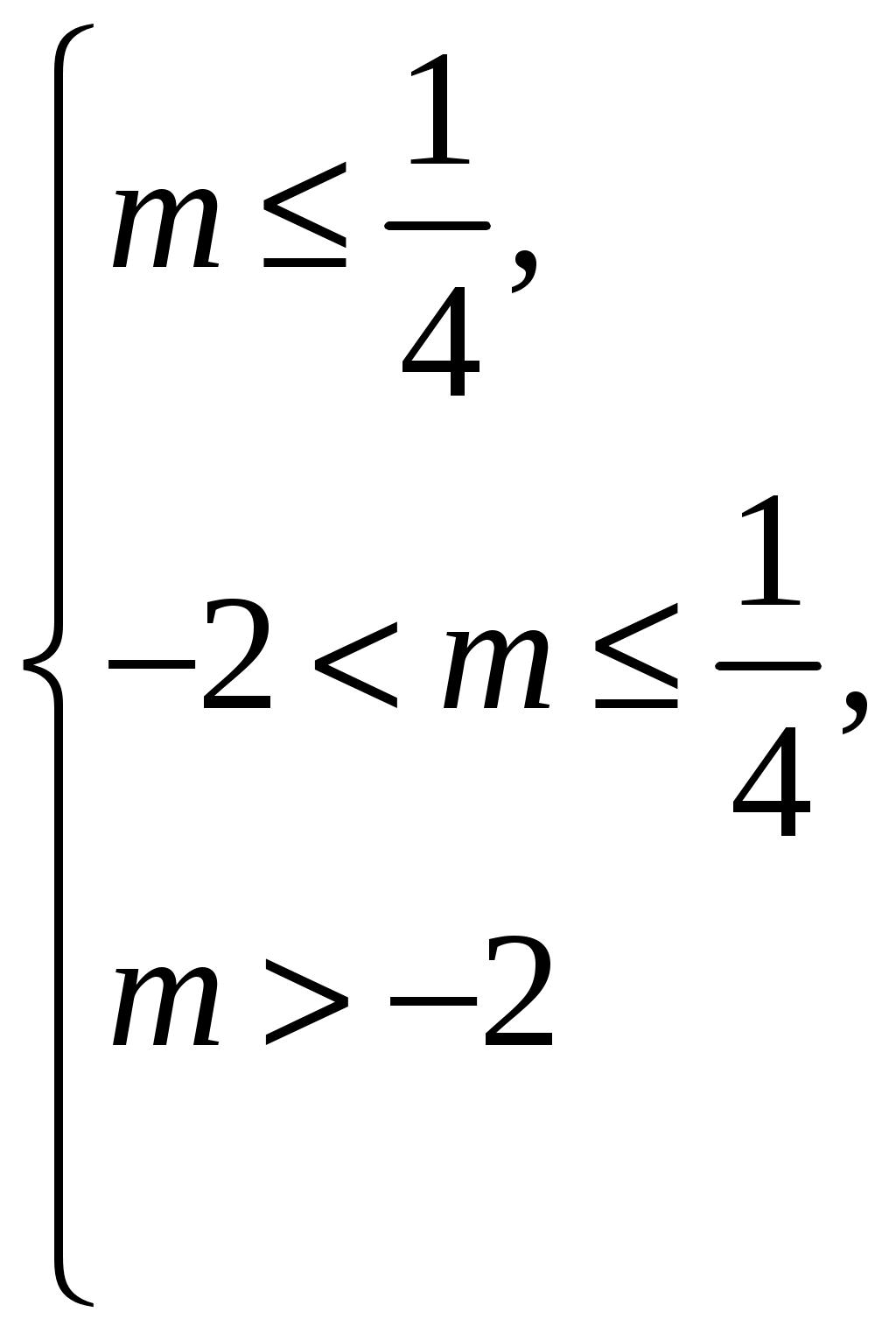
Ответ:
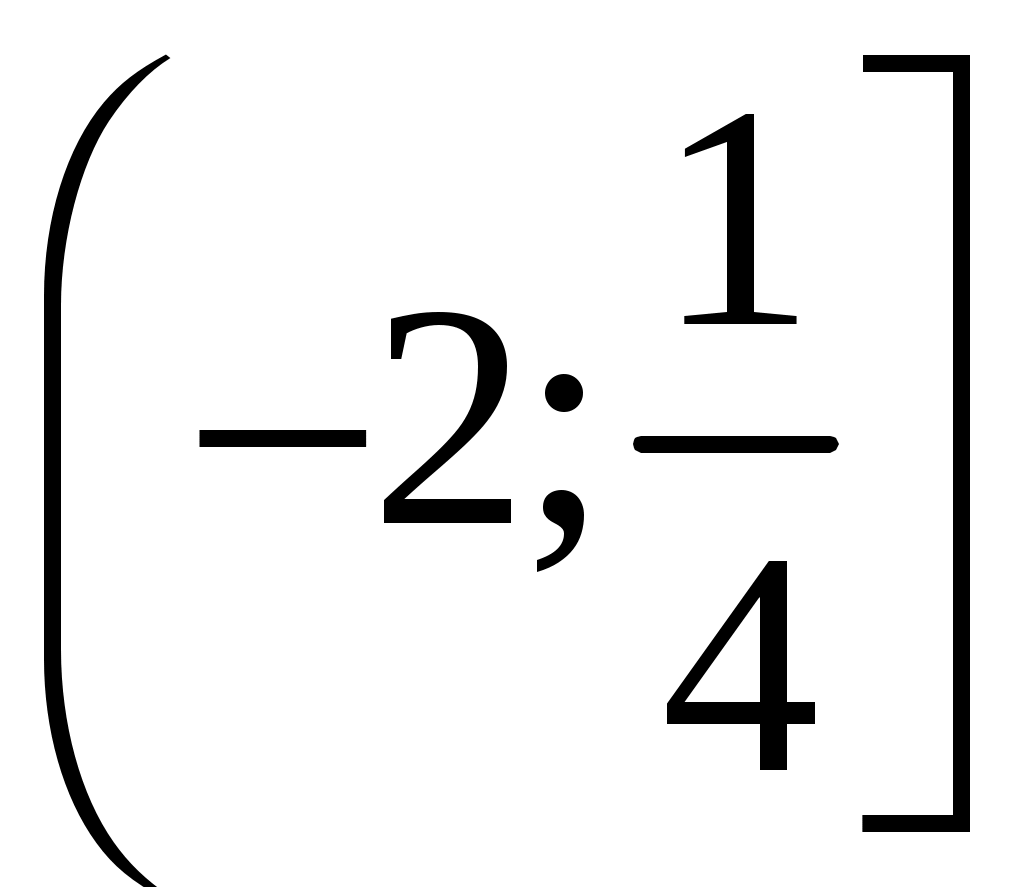 .
.98. При каких mкорни уравнения x22mx+m22m+5=0 по модулю не превосходят 4?
Условие задачи можно сформулировать следующим образом: при каких m
4 х1 х2 4?
Решение:

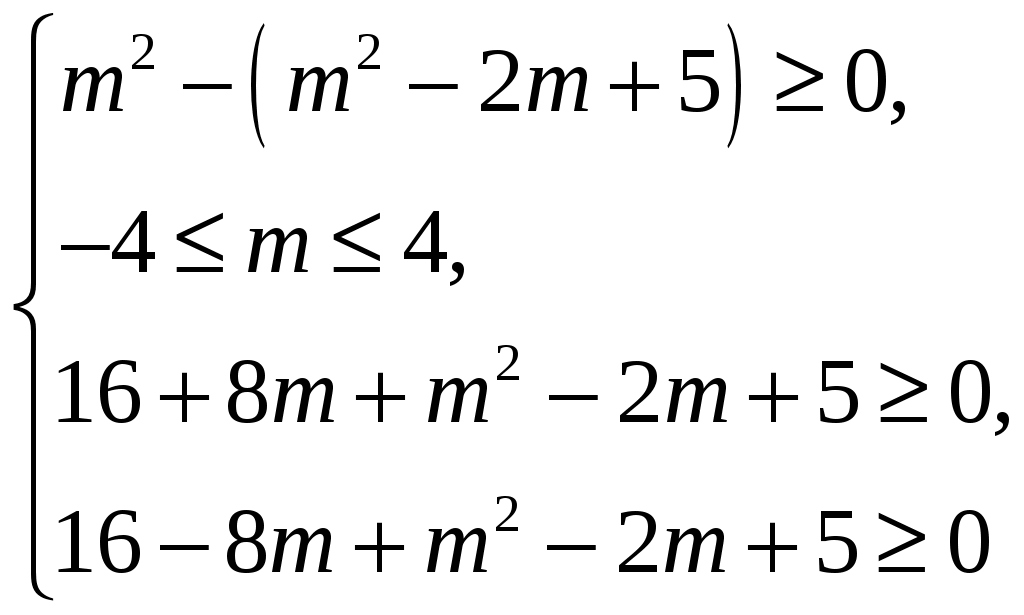

Ответ:
Утверждение 6. Для того, чтобы больший корень квадратного трехчлена принадлежал интервалу (N; M), а меньший не принадлежал, необходимо и достаточно выполнение условий: