Файл: Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc
Добавлен: 09.11.2023
Просмотров: 190
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
при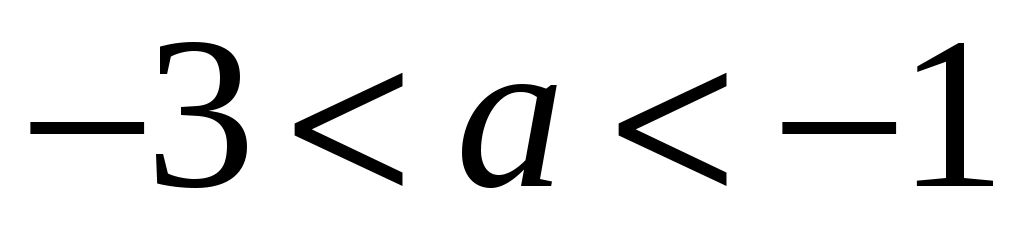
;
при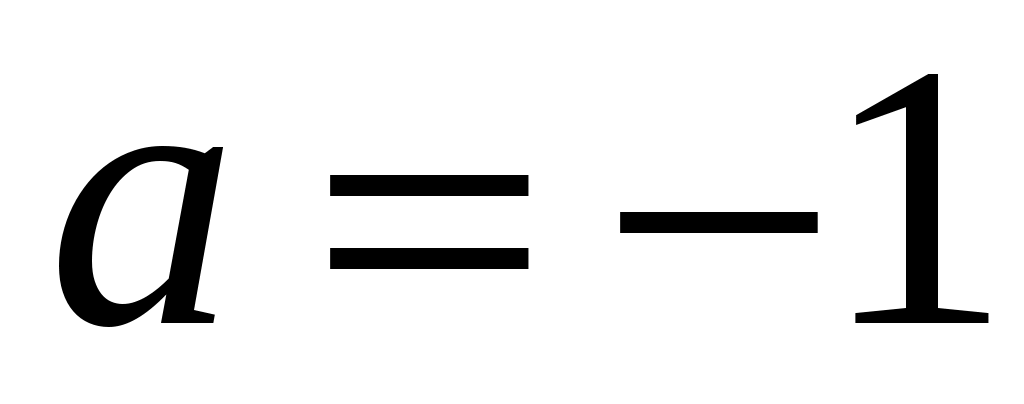
, 
, 
;
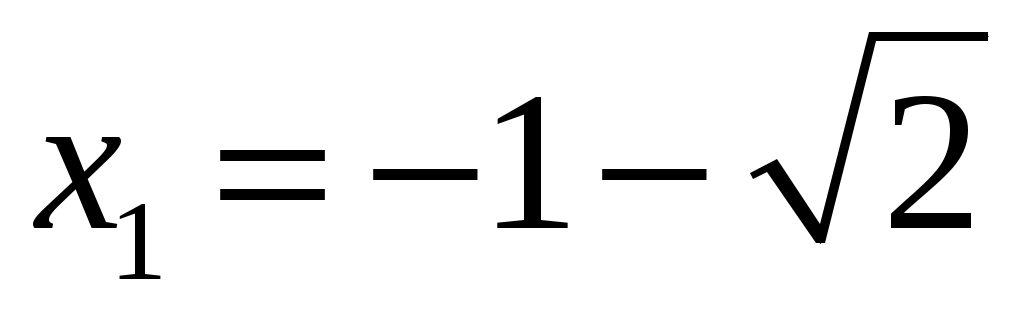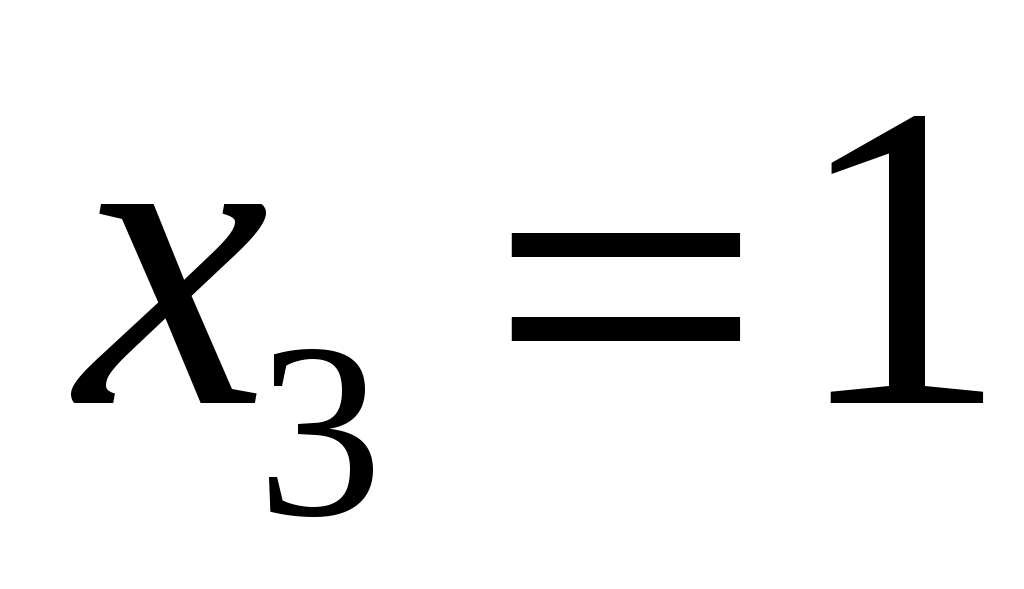при
,
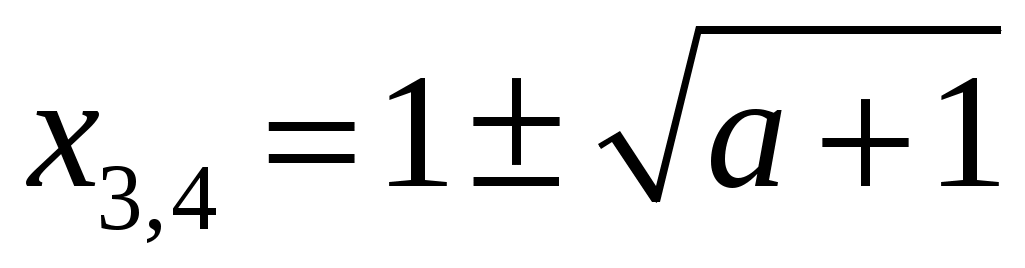
2) Рассматривая этапы решений уравнения (1) с конца, видно, что следует начинать с составления выражения вида (2):
.
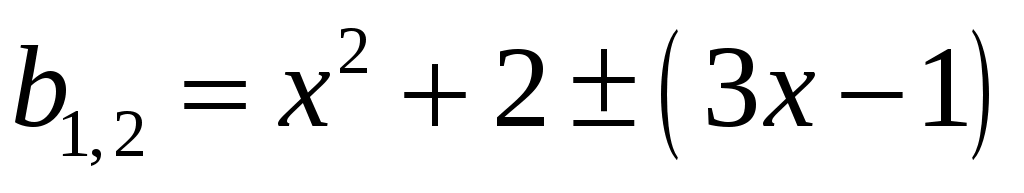Далее запишем два квадратных уравнения с параметром b:
;
.
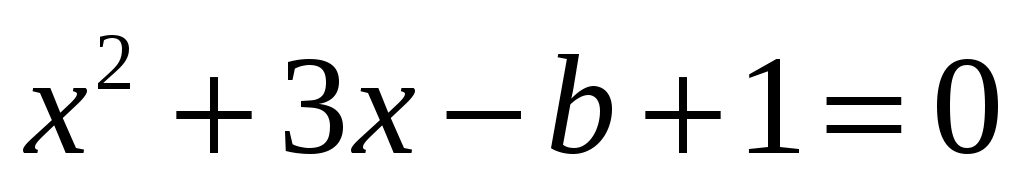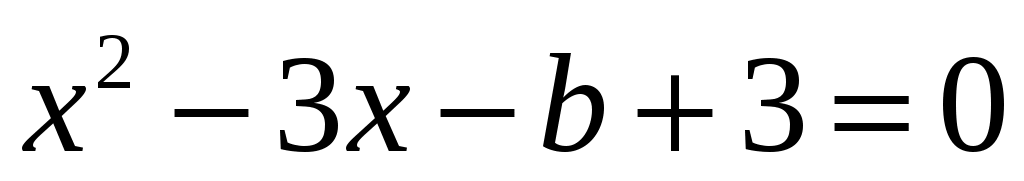Перемножив левые части этих уравнений, получим уравнение четвертой степени относительно x:
,
.
Решается так же, как уравнение (1).
4. Составление задач, обратных данным.
Пример 1.
1) Дано уравнение первой степени
.
Требуется определить область изменения параметра a, если данное уравнение имеет решение: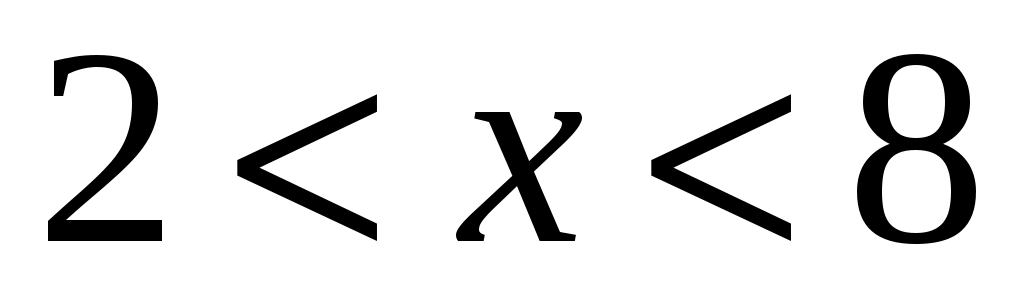
.
Ответ: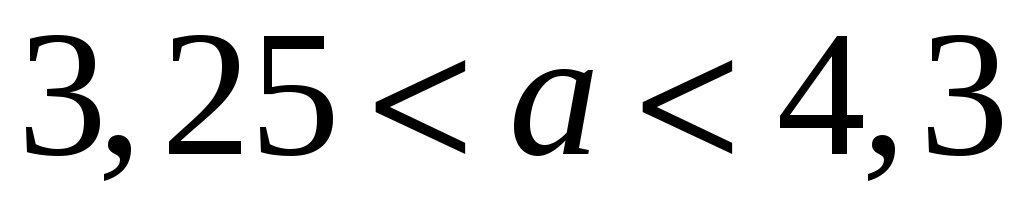
.
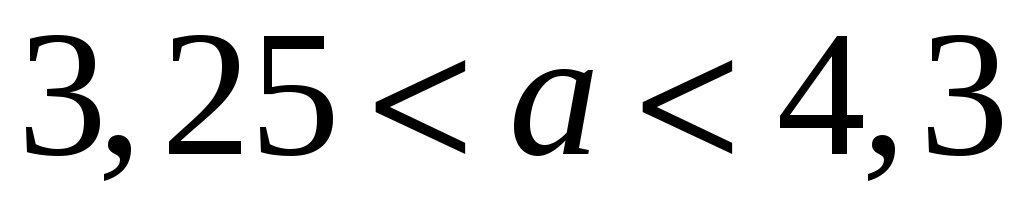2) (Обратная задача). В уравнении параметр a изменяется на промежутке . Определить соответствующую область изменения значений корня.
Пример 2.
1) Пусть решена следующая задача на неравенства:
В каком промежутке должно изменяться число
a, чтобы оба корня уравнения
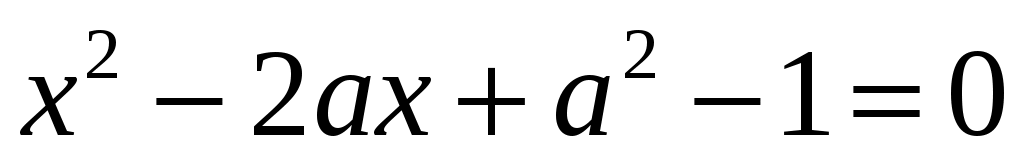были заключены между 2 и 4 ?
Ответ: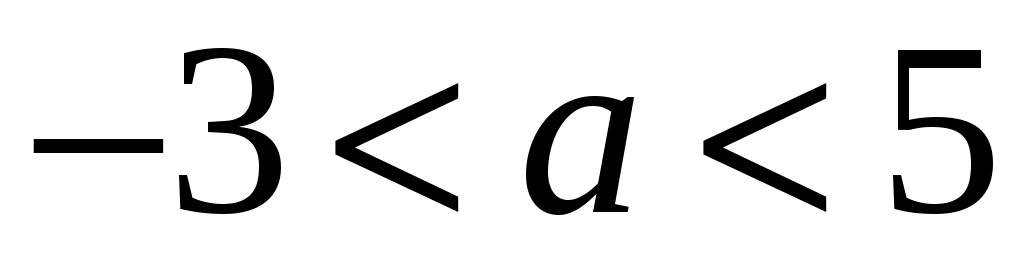
.
2) (Обратная задача). Дано уравнение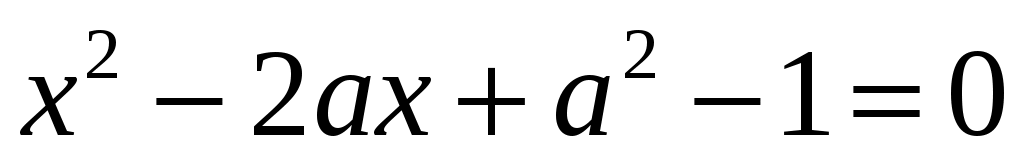 . В каких пределах будут изменяться корни уравнения, если параметр a изменяется в пределах
?
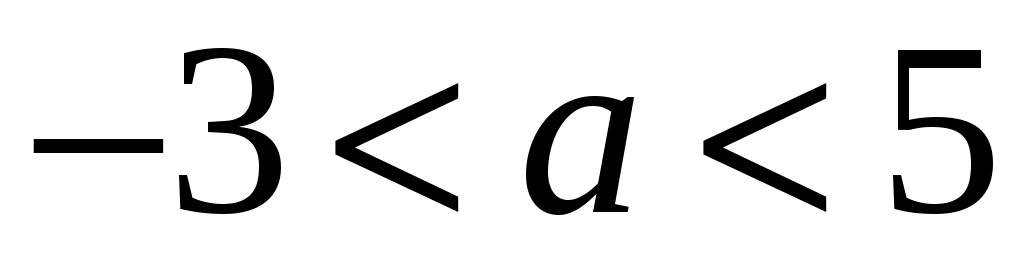Умение решать прямую и обратную задачи является важным критерием достигнутой учеником глубины понимания изучаемого раздела математики, развития творческого мышления, одним из путей саморазвития ума учащихся.
При выборе метода следует продумать такие моменты:
1. Идея метода.
2. Выбор примера для первого знакомства.
3. Способ выполнения анализа условия с целью определения метода решения.
4. Возможности самоконтроля.
5. Методы усложнения заданий.
6. Подготовка банка заданий.
7. Стереотипы мышления, которые мешают при реализации метода и способы их преодоления.
Когда закончена методическая разработка темы, следует переходить к составлению лекции для учащихся. Очевидны следующие требования к школьной лекции:
1. Лекция должна быть интересной для учащихся и для учителя.
2. Научный уровень лекции должен соответствовать уровню развития учащихся класса.
3. Лекция должна быть обучающей, развивающей и воспитывающей.
4. Тема лекции должна естественным образом вытекать из ранее изученного и прокладывать тропинку к последующему.
5. Лекция должна быть совместным делом учащихся и учителя.
6. Лекция должна быть емкой, целостной, размерной, ритмичной, обстоятельной.
7. Главные мысли должны быть повторены несколько раз, выписаны аккуратно на доске и законспектированы учениками.
Специальные графические средства (подчеркивание, выделение) помогают представить конспектируемый материал в наиболее запоминающейся форме.
Основная часть лекции сопровождается вопросами к классу "А как вы думаете?" и т.п. Такие вопросы стимулируют учащихся к активной работе на лекции, помогают им не "выключаться" из процесса познания.
Одно из главных правил-на лекции должны быть вопросы, т.к. способность задавать вопросы является верным признаком активной мыслительной деятельности.
Для урока решения ключевых задач выбираются задачи, соответствующие следующим критериям:
1. Соответствие данной теме.
2. Степень использования при изучении последующих тем.
3. Затраты времени по обучению учащихся решению задач.
4. Оптимальность алгоритмов решения задач.
5. Возможность поразить учащихся красотой решения.
Способ выделения ключевых задач основан либо на умениях, которые должны быть сформированы у учеников после изучения темы, либо на методах решения задач по изучаемой теме.
При определении последовательности ключевых задач учитываются следующие рекомендации:
1. Начинать лучше всего с самых простых ключевых задач.
2. Те ключевые задачи, которые связаны с предыдущей темой, включать в число первых, а используемые в последующих темах разбирать позднее.
3. Самые красивые задачи отнести на вторую часть урока.
4. Чередовать задачи, требующие обширных записей, с теми, которые не требуют громоздких обоснований.
При разборе решений ключевых задач лучше обратиться к лекции. "Размышляя вслух", учитель знакомит ребят с логическими приемами, на основе которых выбирается тот или иной подход к решению. Для того, чтобы убедиться, что учащиеся поняли, можно обратиться к конкретному ученику с предложением рассказать решение ключевой задачи.
К основным задачам урока решения обучающих задач можно отнести:
1. Ознакомление школьников с решениями задач, сводящихся к решению ключевых;
2. Систематизацию методов решения задач по теме;
3. Обучение решению задач по теме в ходе специальных упражнений.
В планируемой системе обучающих задач должны быть представлены:
1. Задачи на распознавание (т.е. задачи, в которых следует распознать ту или иную ключевую задачу);
2. Задачи на реализацию методов;
3. Задачи на применение (в них отрабатываемая задача служит вспомогательной при решении другой задачи).
Успех урока зависит от таких факторов: соответствует ли система обучающих задач особенностям класса ;правильно ли организована работа по систематизации; известны ли затруднения учеников.
В связи с тем, что программой не отведено специальное время на решение задач с параметрами, практикуются долгосрочные домашние задания. Обычно срок выполнения – 7-10 дней. По окончании этого срока на стенде в кабинете вывешивается решение предложенных задач, на текущем уроке делается краткий анализ домашнего задания, назначаются консультанты. Тема развивается по спирали, пронизывая программный материал, поэтому задачи с параметрами включаются либо последним номером в текущую самостоятельную или контрольную работу, либо как дополнительная задача. В течение года учащимся предлагается выполнить несколько проверочных работ, проверяющих навыки решения ключевых задач, а также домашняя контрольная работа, в которую уже включены задачи разной степени сложности. В конце года проводится итоговая контрольная работа
Несмотря на то, что в обучении математики в 5-6 классах встречаются буквенные выражения с одной или несколькими буквами (в частности, в вычислениях по формулам, при записи свойств арифметических действий), в упражнениях, направленных на отработку навыков преобразования буквенных выражений, решения уравнений и т.п., как правило, рассматриваются выражения лишь с одной буквой. Поэтому в самом начале знакомства с параметром (термин дается без определения; записывается на доске и в тетрадях учащихся, включается в словарную работу) у учеников возникает некий психологический барьер, который обусловлен противоречивыми характеристиками параметра. С одной стороны, параметр в уравнении, неравенстве, следует считать величиной известной, а с другой-конкретное значение параметра неизвестно. С одной стороны, параметр является величиной постоянной, а с другой-он может принимать различные значения. Получается, что параметр в уравнении-это неизвестная известная, переменная постоянная величина. Этот "каламбур" очень точно отражает существо тех сложностей, которые нужно преодолеть ученикам. Учитель должен не спеша, скрупулезно и обязательно доброжелательно разъяснить младшим школьникам такой сложный вопрос, обильно сопровождая его различными примерами.
Целесообразно включать как в устные, так и в письменные упражнения задачи такого содержания:
5 класс
Сравните
и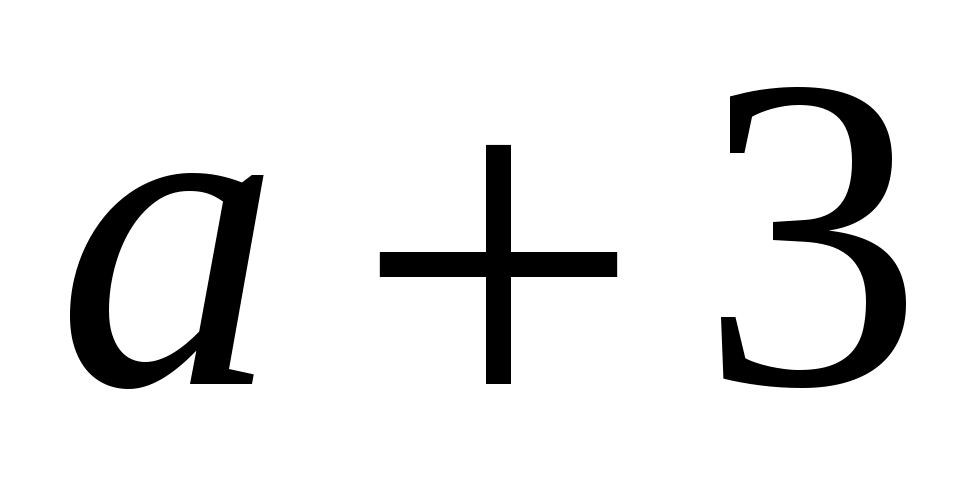 
.
Известно, что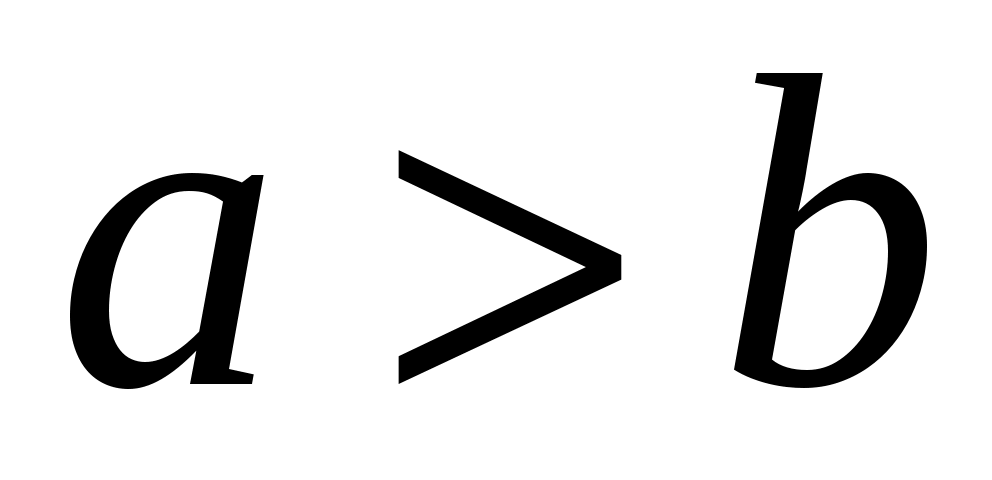
. Расположите в порядке возрастания числа:
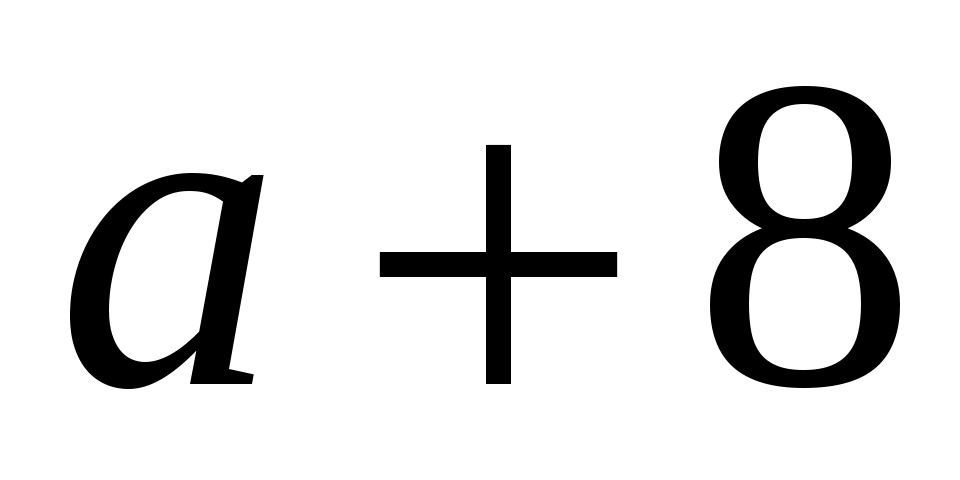
при
;при
, , ;при
, 2) Рассматривая этапы решений уравнения (1) с конца, видно, что следует начинать с составления выражения вида (2):
.Далее запишем два квадратных уравнения с параметром b:
; .Перемножив левые части этих уравнений, получим уравнение четвертой степени относительно x:
, .Решается так же, как уравнение (1).
4. Составление задач, обратных данным.
Пример 1.
1) Дано уравнение первой степени
. Требуется определить область изменения параметра a, если данное уравнение имеет решение:
.Ответ:
.2) (Обратная задача). В уравнении
параметр a изменяется на промежутке . Определить соответствующую область изменения значений корня.Пример 2.
1) Пусть решена следующая задача на неравенства:
В каком промежутке должно изменяться число
a, чтобы оба корня уравнения
были заключены между 2 и 4 ?Ответ:
.2) (Обратная задача). Дано уравнение
. В каких пределах будут изменяться корни уравнения, если параметр a изменяется в пределах ?Умение решать прямую и обратную задачи является важным критерием достигнутой учеником глубины понимания изучаемого раздела математики, развития творческого мышления, одним из путей саморазвития ума учащихся.
При выборе метода следует продумать такие моменты:
1. Идея метода.
2. Выбор примера для первого знакомства.
3. Способ выполнения анализа условия с целью определения метода решения.
4. Возможности самоконтроля.
5. Методы усложнения заданий.
6. Подготовка банка заданий.
7. Стереотипы мышления, которые мешают при реализации метода и способы их преодоления.
Когда закончена методическая разработка темы, следует переходить к составлению лекции для учащихся. Очевидны следующие требования к школьной лекции:
1. Лекция должна быть интересной для учащихся и для учителя.
2. Научный уровень лекции должен соответствовать уровню развития учащихся класса.
3. Лекция должна быть обучающей, развивающей и воспитывающей.
4. Тема лекции должна естественным образом вытекать из ранее изученного и прокладывать тропинку к последующему.
5. Лекция должна быть совместным делом учащихся и учителя.
6. Лекция должна быть емкой, целостной, размерной, ритмичной, обстоятельной.
7. Главные мысли должны быть повторены несколько раз, выписаны аккуратно на доске и законспектированы учениками.
Специальные графические средства (подчеркивание, выделение) помогают представить конспектируемый материал в наиболее запоминающейся форме.
Основная часть лекции сопровождается вопросами к классу "А как вы думаете?" и т.п. Такие вопросы стимулируют учащихся к активной работе на лекции, помогают им не "выключаться" из процесса познания.
Одно из главных правил-на лекции должны быть вопросы, т.к. способность задавать вопросы является верным признаком активной мыслительной деятельности.
Для урока решения ключевых задач выбираются задачи, соответствующие следующим критериям:
1. Соответствие данной теме.
2. Степень использования при изучении последующих тем.
3. Затраты времени по обучению учащихся решению задач.
4. Оптимальность алгоритмов решения задач.
5. Возможность поразить учащихся красотой решения.
Способ выделения ключевых задач основан либо на умениях, которые должны быть сформированы у учеников после изучения темы, либо на методах решения задач по изучаемой теме.
При определении последовательности ключевых задач учитываются следующие рекомендации:
1. Начинать лучше всего с самых простых ключевых задач.
2. Те ключевые задачи, которые связаны с предыдущей темой, включать в число первых, а используемые в последующих темах разбирать позднее.
3. Самые красивые задачи отнести на вторую часть урока.
4. Чередовать задачи, требующие обширных записей, с теми, которые не требуют громоздких обоснований.
При разборе решений ключевых задач лучше обратиться к лекции. "Размышляя вслух", учитель знакомит ребят с логическими приемами, на основе которых выбирается тот или иной подход к решению. Для того, чтобы убедиться, что учащиеся поняли, можно обратиться к конкретному ученику с предложением рассказать решение ключевой задачи.
К основным задачам урока решения обучающих задач можно отнести:
1. Ознакомление школьников с решениями задач, сводящихся к решению ключевых;
2. Систематизацию методов решения задач по теме;
3. Обучение решению задач по теме в ходе специальных упражнений.
В планируемой системе обучающих задач должны быть представлены:
1. Задачи на распознавание (т.е. задачи, в которых следует распознать ту или иную ключевую задачу);
2. Задачи на реализацию методов;
3. Задачи на применение (в них отрабатываемая задача служит вспомогательной при решении другой задачи).
Успех урока зависит от таких факторов: соответствует ли система обучающих задач особенностям класса ;правильно ли организована работа по систематизации; известны ли затруднения учеников.
В связи с тем, что программой не отведено специальное время на решение задач с параметрами, практикуются долгосрочные домашние задания. Обычно срок выполнения – 7-10 дней. По окончании этого срока на стенде в кабинете вывешивается решение предложенных задач, на текущем уроке делается краткий анализ домашнего задания, назначаются консультанты. Тема развивается по спирали, пронизывая программный материал, поэтому задачи с параметрами включаются либо последним номером в текущую самостоятельную или контрольную работу, либо как дополнительная задача. В течение года учащимся предлагается выполнить несколько проверочных работ, проверяющих навыки решения ключевых задач, а также домашняя контрольная работа, в которую уже включены задачи разной степени сложности. В конце года проводится итоговая контрольная работа
Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 5-8 классов
5-6 класс. Пропедевтика
Несмотря на то, что в обучении математики в 5-6 классах встречаются буквенные выражения с одной или несколькими буквами (в частности, в вычислениях по формулам, при записи свойств арифметических действий), в упражнениях, направленных на отработку навыков преобразования буквенных выражений, решения уравнений и т.п., как правило, рассматриваются выражения лишь с одной буквой. Поэтому в самом начале знакомства с параметром (термин дается без определения; записывается на доске и в тетрадях учащихся, включается в словарную работу) у учеников возникает некий психологический барьер, который обусловлен противоречивыми характеристиками параметра. С одной стороны, параметр в уравнении, неравенстве, следует считать величиной известной, а с другой-конкретное значение параметра неизвестно. С одной стороны, параметр является величиной постоянной, а с другой-он может принимать различные значения. Получается, что параметр в уравнении-это неизвестная известная, переменная постоянная величина. Этот "каламбур" очень точно отражает существо тех сложностей, которые нужно преодолеть ученикам. Учитель должен не спеша, скрупулезно и обязательно доброжелательно разъяснить младшим школьникам такой сложный вопрос, обильно сопровождая его различными примерами.
Целесообразно включать как в устные, так и в письменные упражнения задачи такого содержания:
5 класс
Тема "Натуральные числа"
Сравните
и .Известно, что
. Расположите в порядке возрастания числа: