Файл: Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc
Добавлен: 09.11.2023
Просмотров: 185
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2+3x+(k27k+12) равно нулю?
Ответ: 3; 4.
61. При каких значениях k сумма корней квадратного уравнения x2+(k2+4k 5)x k равна нулю?
Ответ: 1.
62. При каких значениях p и q корни уравнения x2+px+q=0 равны 2p и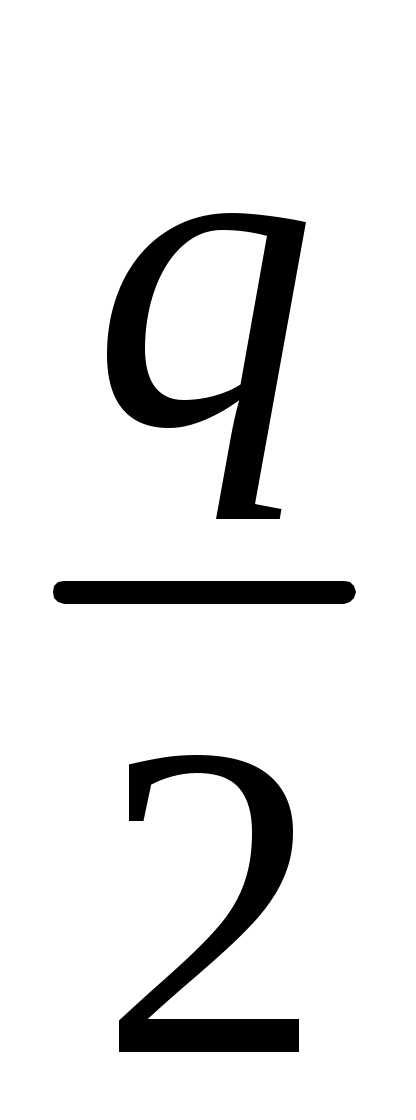 ?
?
Ответ: p=q=0 или p=1, q=6.
Более подробно следует остановиться на задачах такого содержания.
63. При каких значениях a оба корня уравнения x22ax+4=0 положительны?
Обсуждаем. Для того, чтобы оба корня уравнения были положительны, нужно, во-первых, чтобы оно имело два корня, а для этого необходимо, чтобы дискриминант был больше нуля. Во-вторых, так как свободный член положительный, то оба корня имеют одинаковые знаки, а поэтому, чтобы они имели знаки "плюс", нужно, чтобы коэффициент среднего члена был отрицательный.
Разбив требование задачи на указанные две части, мы разбиваем и саму задачу на две более простые:
1. При каких значениях a дискриминант уравнения положительный?
2. При каких значениях a коэффициент среднего члена уравнения отрицательный?
Решение:
D=a2 4, a2 4>0, a2>4, a>2, a<2 или a>2.
2a<0, a>0.
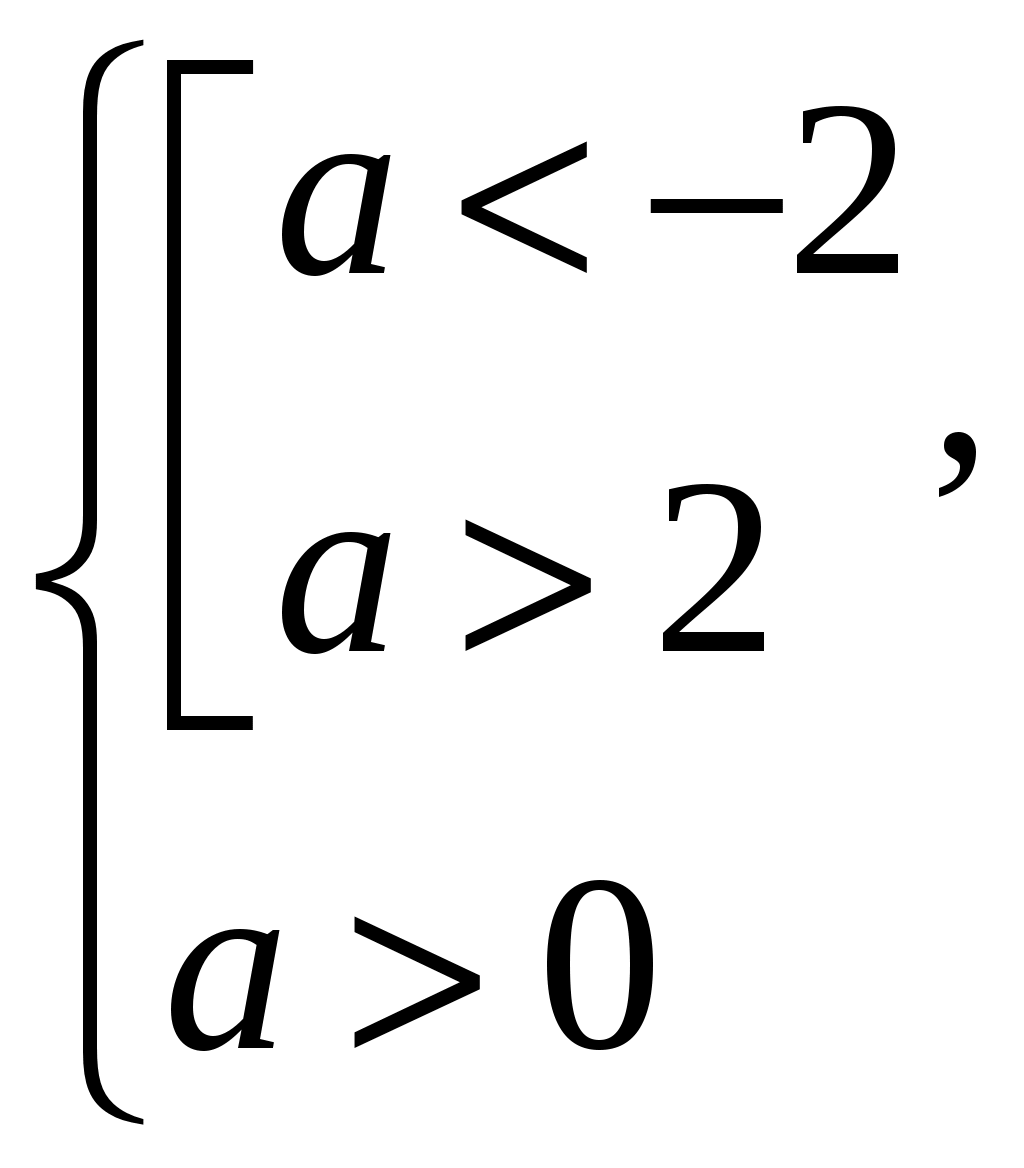 a>2.
a>2.
Ответ: a>2.
64. При каких значениях параметра a уравнение ax2 4x+a=0 имеет:
а) положительные корни;
б) отрицательные корни;
в) корень, равный нулю?
Ответ: а) 0 2; б) 2 a<0; в) a=0.
65. В уравнении x2+ax+12=0 определить a таким образом, чтобы разность корней равнялась единице.
Решение: x2 x1=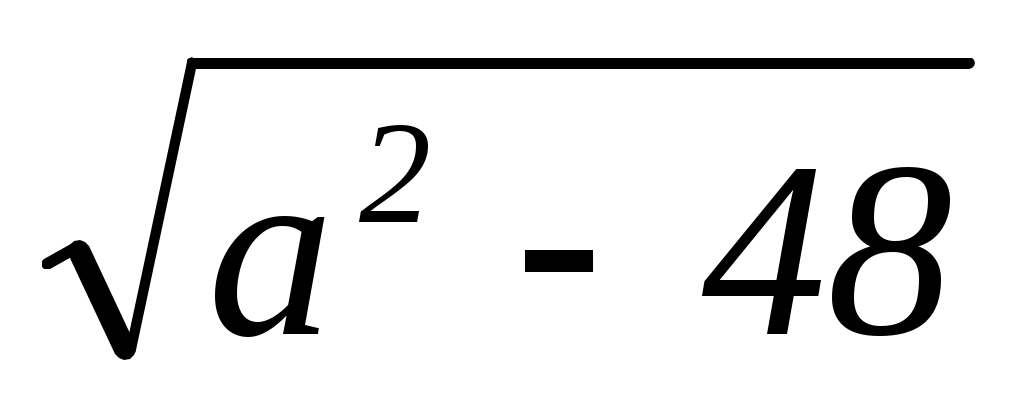 = 1, a= 7.
= 1, a= 7.
Ответ: a= 7.
Разнообразны задачи с применением формул сокращенного умножения.
66. Корниуравнения x2 3ax+a2=0 таковы, что x1 2+ x2 2=112. Найти a.
Решение:
D=9a2 4a2=5a2, D 0 при любых a.
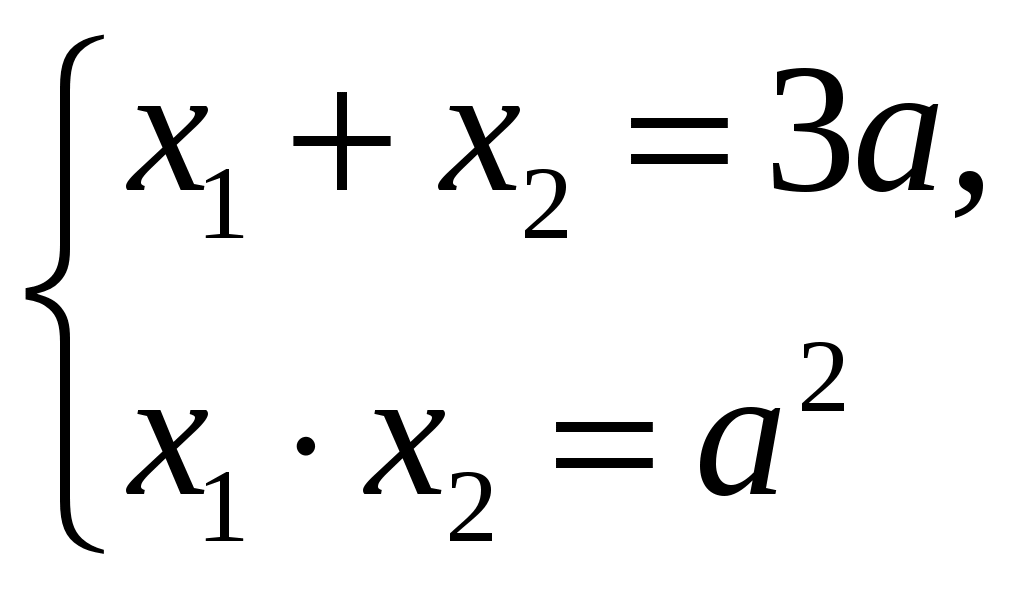 ,
,
x12+ x22=(x1+x2)2 2x1 x2=(3a)2 2a2=7a2=112; a2=16, a= 4.
Ответ: 4.
67. В уравнении 3x2+ax+2=0 определить a таким образом, чтобы корни уравнения были действительными, а сумма кубов корней равнялась удвоенной сумме корней.
Решение:
D>0, D=a2 24;
a2 24>0, a2>24; a>2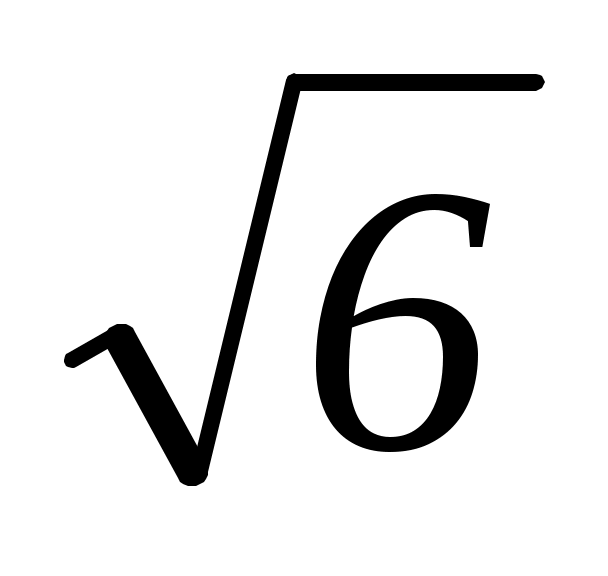 .
.
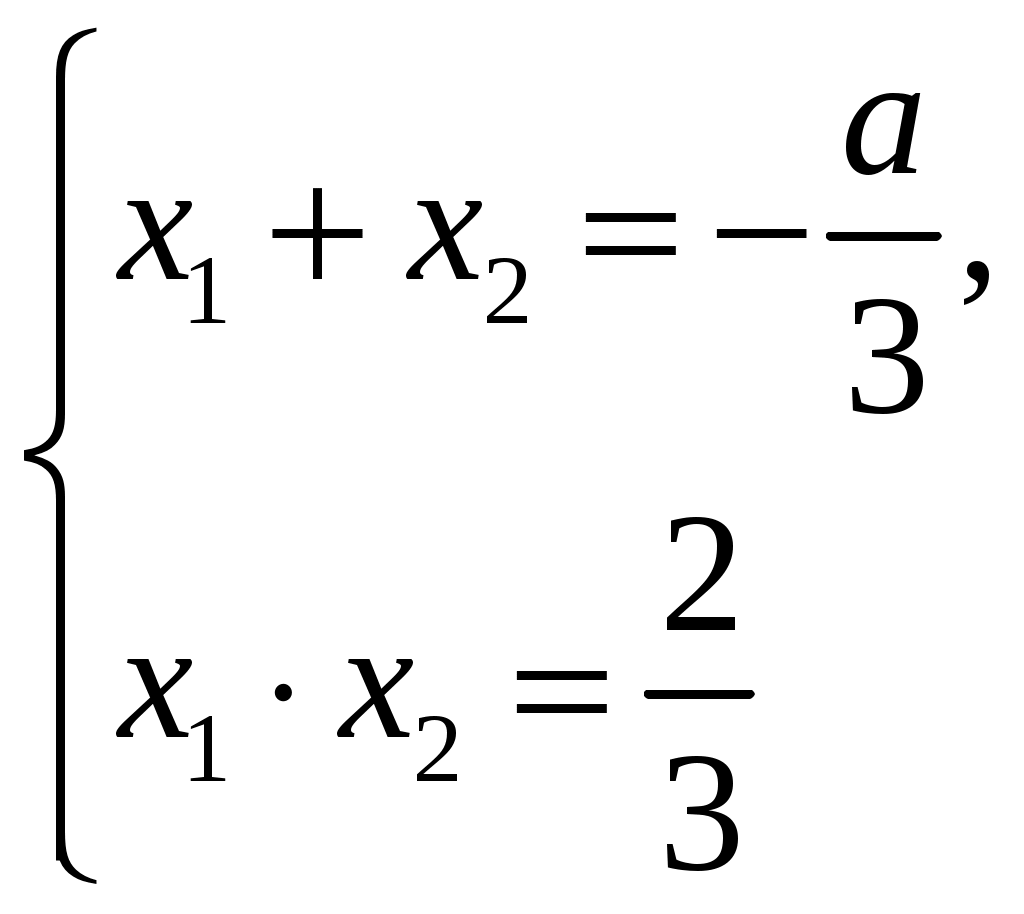
x13+x23=(x1+x2)(x12+ x22 x1 x2)=(x1+x2)((x1+ x2)2 3x1 x2)=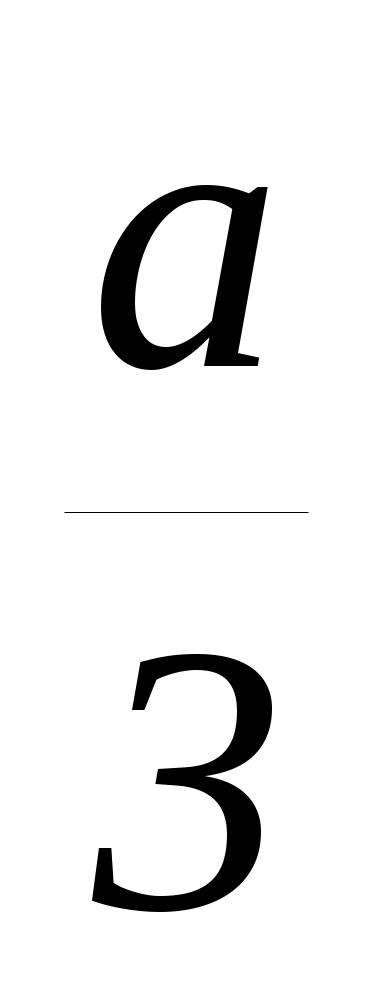 (
( 2).
2).
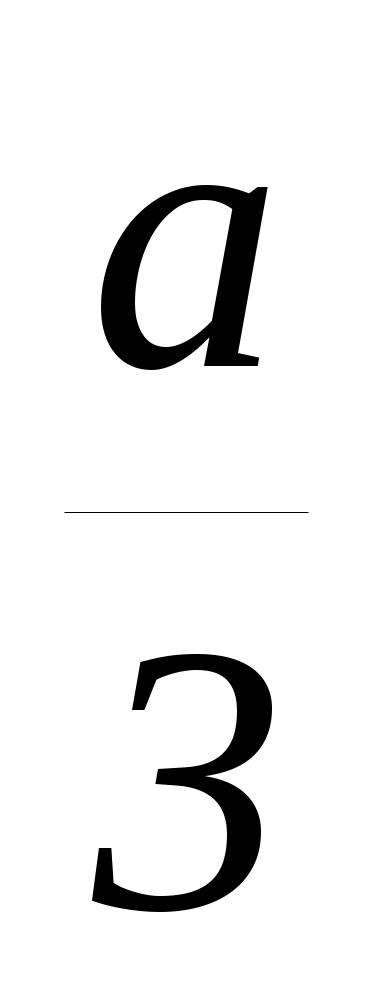 (
( 2)=
2)=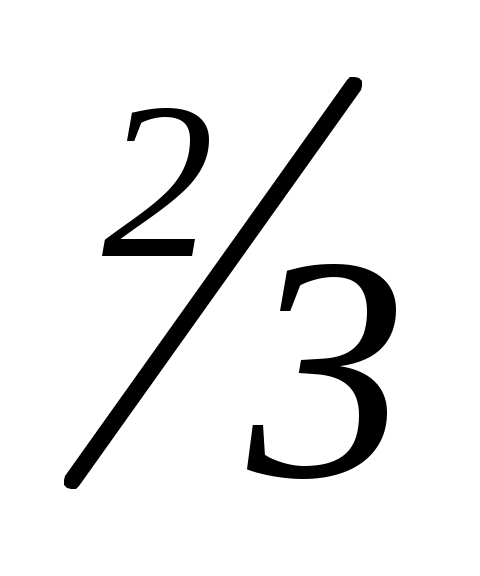 a; a(
a; a( 4)=0; a=0; a= 6.
4)=0; a=0; a= 6.
0<2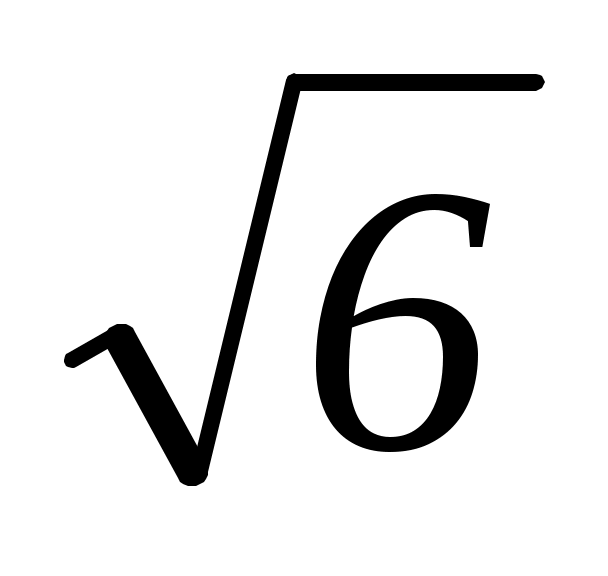 ; 6>2
; 6>2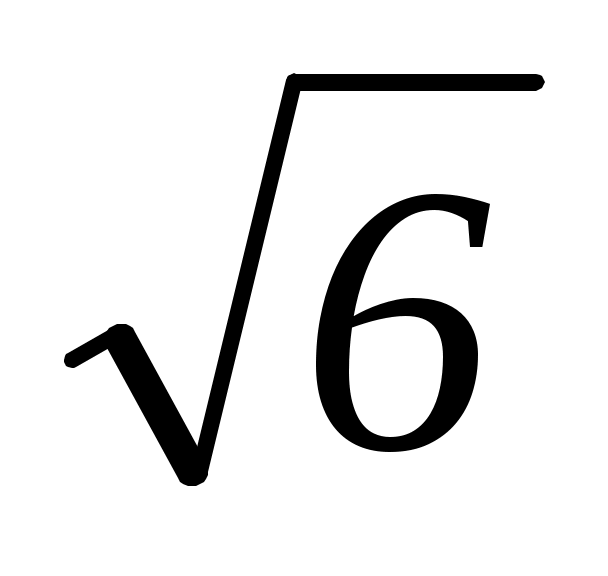 .
.
Ответ: 6.
68. Пусть x1 и x2-корниуравнения x2+px+q=0. Выразить x14+ x24 через p и q.
Решение:
1)x1+x2= p;
x1 x2=q.
2) x14+x24=(x12+ x22)22x12x22=((x1+x2)22x1x2)22x12x22=(p2-2q2)2-2q2=
=p4-4p2q2+2q2.
Ответ: p4-4p2q2+2q2.
69. При каком значении параметра m сумма квадратов корней уравнения x2+(m 1)x+m2 1,5=0 наибольшая?
Ответ: –1.
70. При каком значении параметра m сумма квадратов корней уравнения x2+(2 m)x+m 3=0 наименьшая?
Ответ: 1.
Учащиеся должны самостоятельно уметь решать задачи типа 59, 62, 65. Задачи такого типа целесообразно включать как обязательный материал в текущие самостоятельные и контрольные работы.
Итоги работы за год покажет большая проверочная работа, в которую включены задачи, аналогичные ключевым по всем темам.
Основная цель работы в 9 классе – просто изучить квадратный трехчлен и квадратные неравенства. Учащиеся 9 класса уже готовы к серьезной исследовательской работе, поэтому излагать новый материал можно в виде проблемного диалога между учениками и учителем.
При изучении графиков функций y=ax2+nиy=a(x-m)2 в устную и письменную работу полезно включать задачи такого содержания.
71. Найдите количество целых значений а, при которых абсцисса и ордината вершины параболы y=(x-5-a)2+3-a положительны.
Решение: y=(x-(5+a))2+3-a; х0=5+а; y0=3-a.
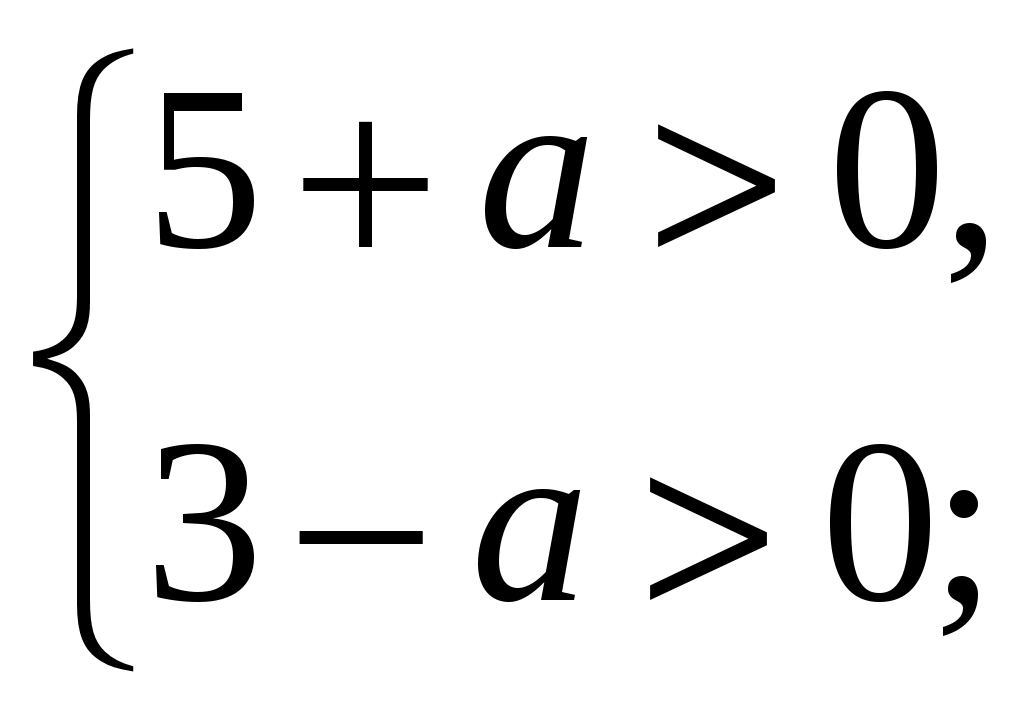
 –5<а<3.
–5<а<3.
Целые значения а: –4; –3; –2; –1; 0; 1; 2.
Ответ: 7.
Изучая график квадратного трехчлена, рассматриваем следующие задачи:
72. При каких m парабола y=mx2-4mх+35 касается оси абсцисс?
Решение: Парабола касается оси абсцисс, если дискриминант равен 0
D1=(2m)2-m35=4m2-35m=4m (m-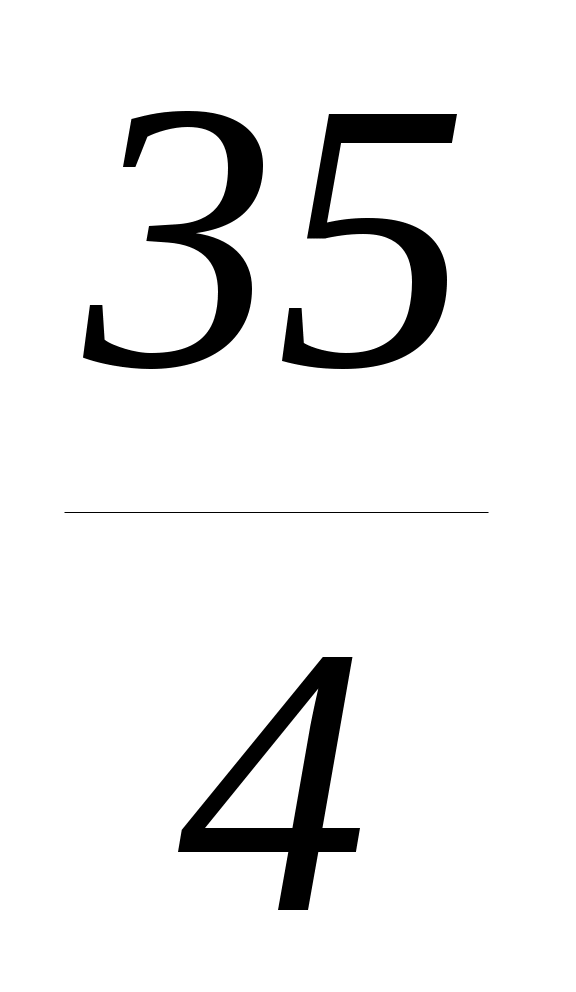 );
);
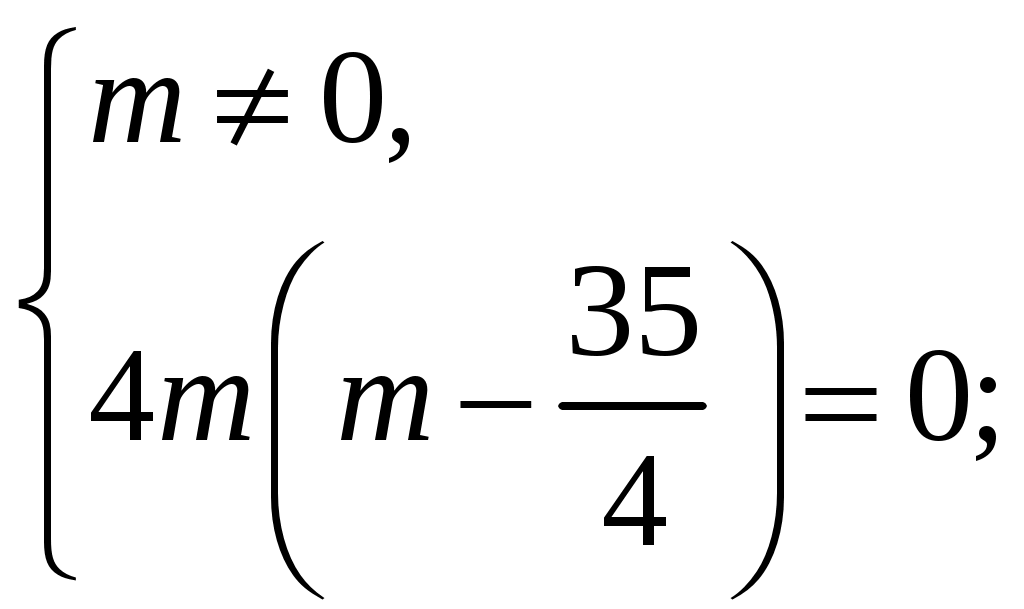
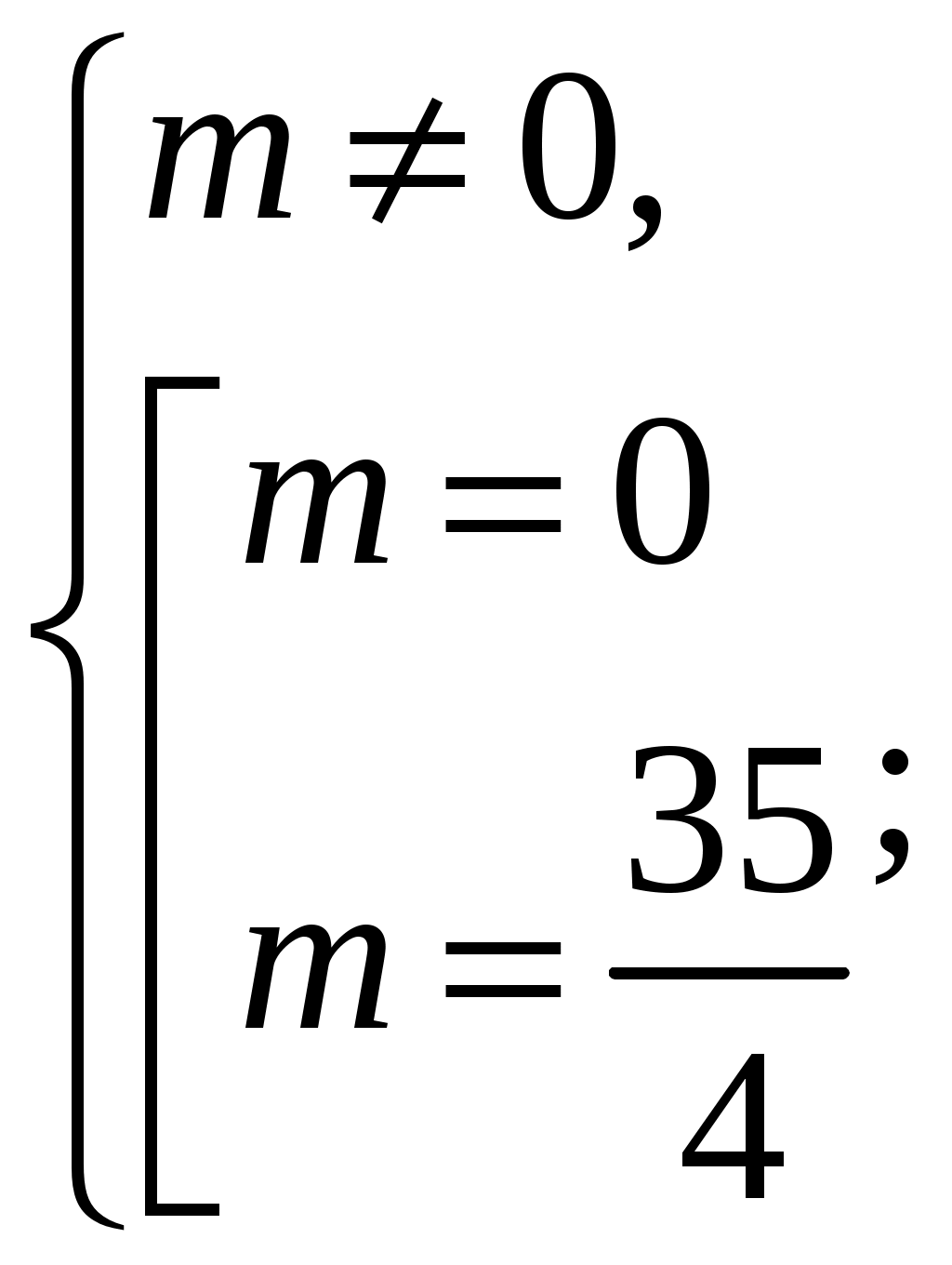
Ответ: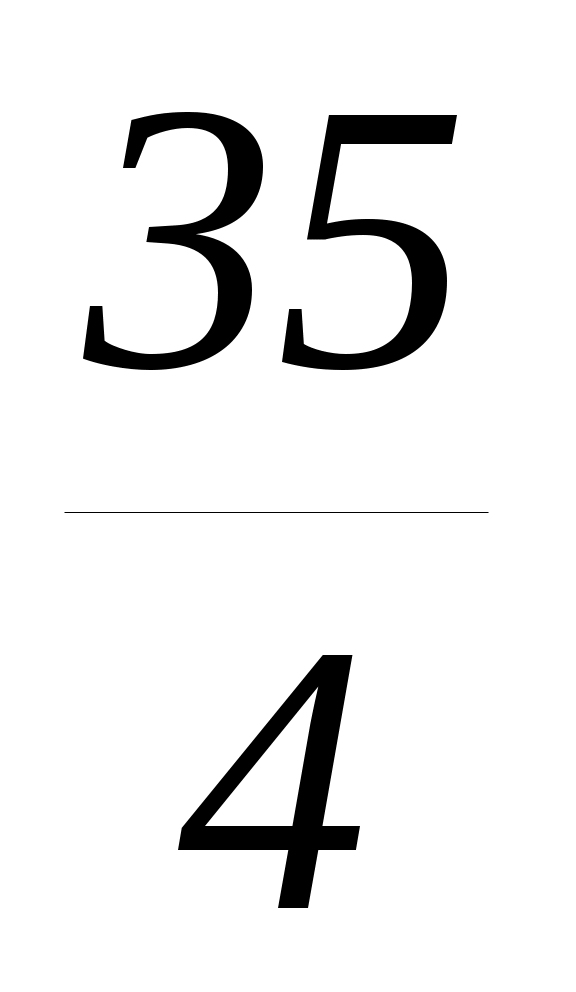 .
.
Замечание. При решении таких задач следует всякий раз акцентировать внимание на том факте, что значение первого коэффициента не должно обращаться в ноль.
73. Найдите значения а и b, при которых точка (1; 1) является вершиной параболы
y=аx2+bх+8.
Решение: Если точка (х0; y0)-вершина параболы, то х0=–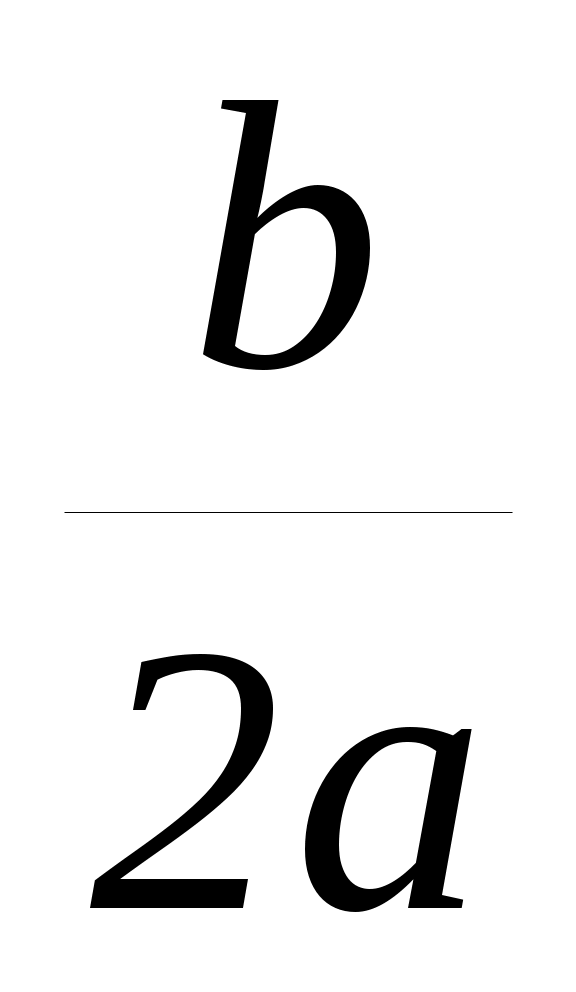 ; y0=y(x0).
; y0=y(x0).
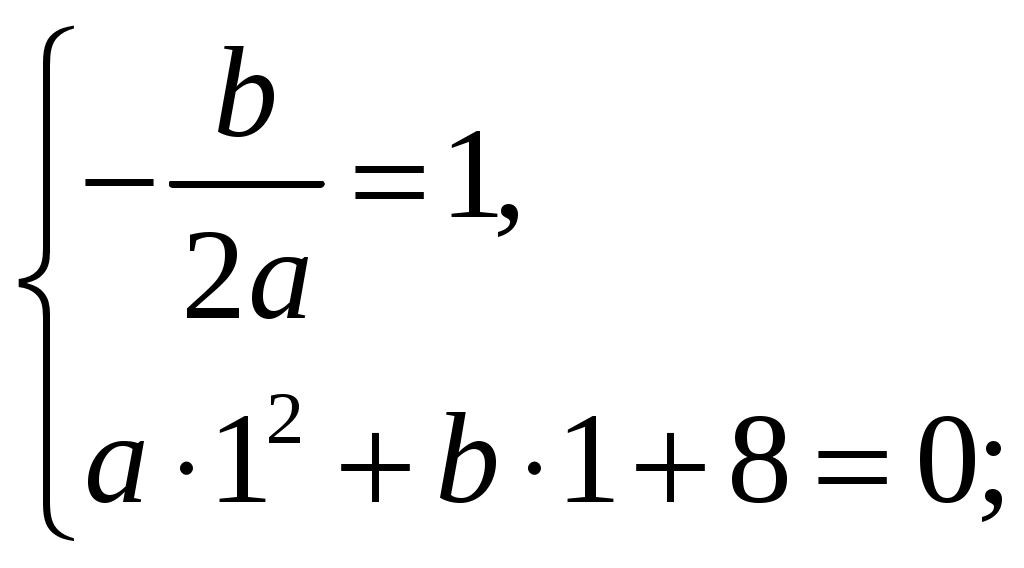
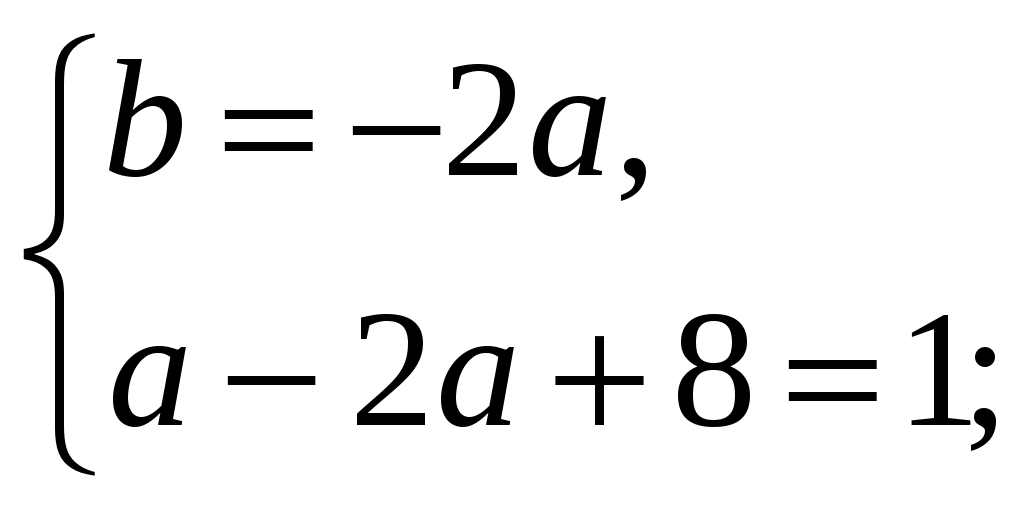
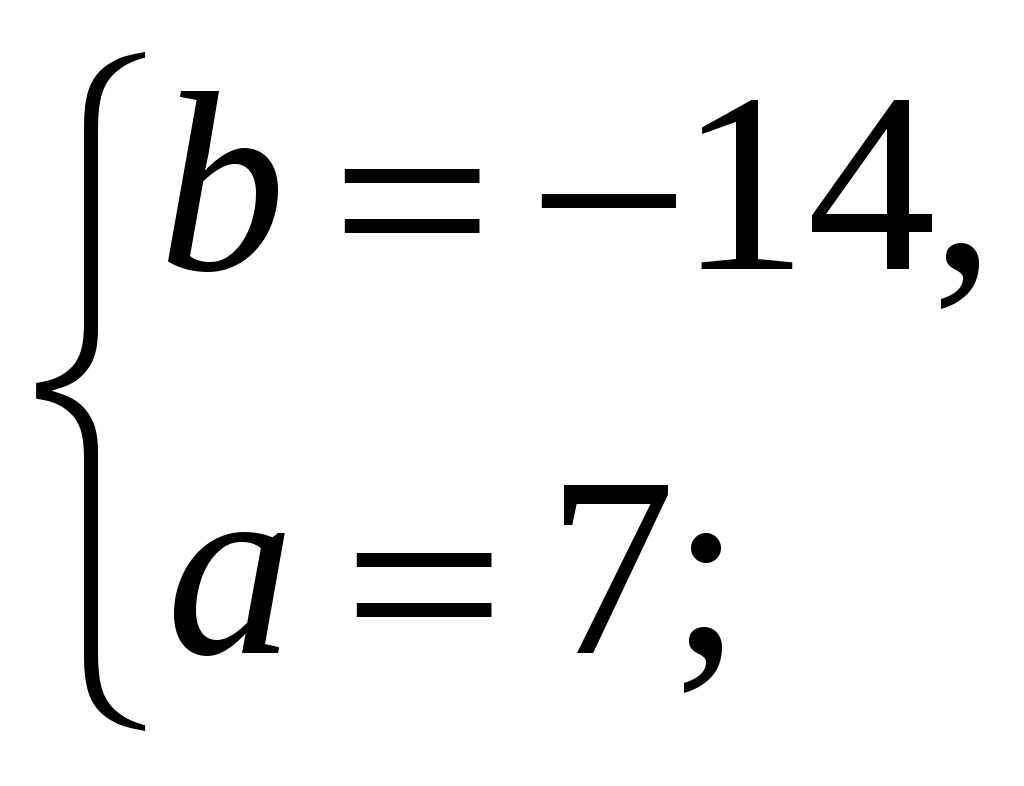
Ответ: а=7; b=–14.
Очень содержательными, по-настоящему развивающими исследователь-ские навыки являются задачи типа:
74. Известно, что парабола y=аx2+bх+с не пересекает ось 0х и a+b+ c< 0. Определить знаки а и с.
Прежде, чем записать решение задачи, рассмотрим утверждения:
1. Если парабола не пересекает ось 0х, то она полностью лежит или над осью, или под осью, то есть при всех х принимает значения одного знака.
2. Значение функции при х=0 равно ее свободному члену, т.е. y(0)=c.
3. Значение функции при х=1 равно сумме коэффициентов y(1)=a+b+c.
Решение:
1) y(1)=a+b+c. Так как a+b+c<0, то y(1)<0.
2) Функция принимает значения одного знака, следовательноy<0 при всех х, т. е. парабола лежит под осью 0х, таким образом а<0,y(0)<0, с<0.
Ответ: а<0; с<0.
75. Квадратный трехчлен аx2+bх+с не имеет корней, а его коэффициенты связаны условием ab+c<0. Определить знак числа с.
Решение:
D<0, следовательно y>0 или y<0 для всех х.
y()=ab+c. Так как ab+c<0, то y()<0, таким образом y<0 для всех х.
с=y(0); y(0)<0, значит с<0.
Ответ: с<0.
76. Известно, что квадратное уравнение аx2+bх+с=0 не имеет корней и a+c<
b. Определить знак с.
Решение: совпадает с решением задачи 76.
Ответ: с<0.
Пока девятиклассники не научились решать квадратные неравенства, им предлагаются задачи простые по технике решения. Важно, чтобы ученики могли грамотно проанализировать условие и вопрос задачи и правильно составить соответствующую систему.
Решение квадратных неравенств с параметрами – один из наиболее сложных вопросов 9 класса. Задачи очень разнообразны по формулировкам и порой достаточно трудоемки, объемны по записи решения, поэтому уже на первых уроках изучения темы "Решение неравенств второй степени с одной переменной" ученики составляют в тетради таблицу, которой активно пользуются сначала при решении числовых неравенств, а потом и неравенств с параметрами.
Изучив графический способ решения квадратных неравенств и рассмотрев примеры всех возможных типов, девятиклассники делают вывод, что возможны шесть случаев положения параболы относительно оси 0х. Факторы, влияющие на положение параболы-знак первого коэффициента и знак дискриминанта. Исследуем решение всех случаев.
Решение квадратных неравенств
f (x)>0(x)=Ax2+Bx+C, где А, В, С – некоторые числа или выражения,
зависящие только от параметра, причем А 0, х1 , х2-нули функции.
Ответ: 3; 4.
61. При каких значениях k сумма корней квадратного уравнения x2+(k2+4k 5)x k равна нулю?
Ответ: 1.
62. При каких значениях p и q корни уравнения x2+px+q=0 равны 2p и
Ответ: p=q=0 или p=1, q=6.
Более подробно следует остановиться на задачах такого содержания.
63. При каких значениях a оба корня уравнения x22ax+4=0 положительны?
Обсуждаем. Для того, чтобы оба корня уравнения были положительны, нужно, во-первых, чтобы оно имело два корня, а для этого необходимо, чтобы дискриминант был больше нуля. Во-вторых, так как свободный член положительный, то оба корня имеют одинаковые знаки, а поэтому, чтобы они имели знаки "плюс", нужно, чтобы коэффициент среднего члена был отрицательный.
Разбив требование задачи на указанные две части, мы разбиваем и саму задачу на две более простые:
1. При каких значениях a дискриминант уравнения положительный?
2. При каких значениях a коэффициент среднего члена уравнения отрицательный?
Решение:
D=a2 4, a2 4>0, a2>4, a>2, a<2 или a>2.
2a<0, a>0.
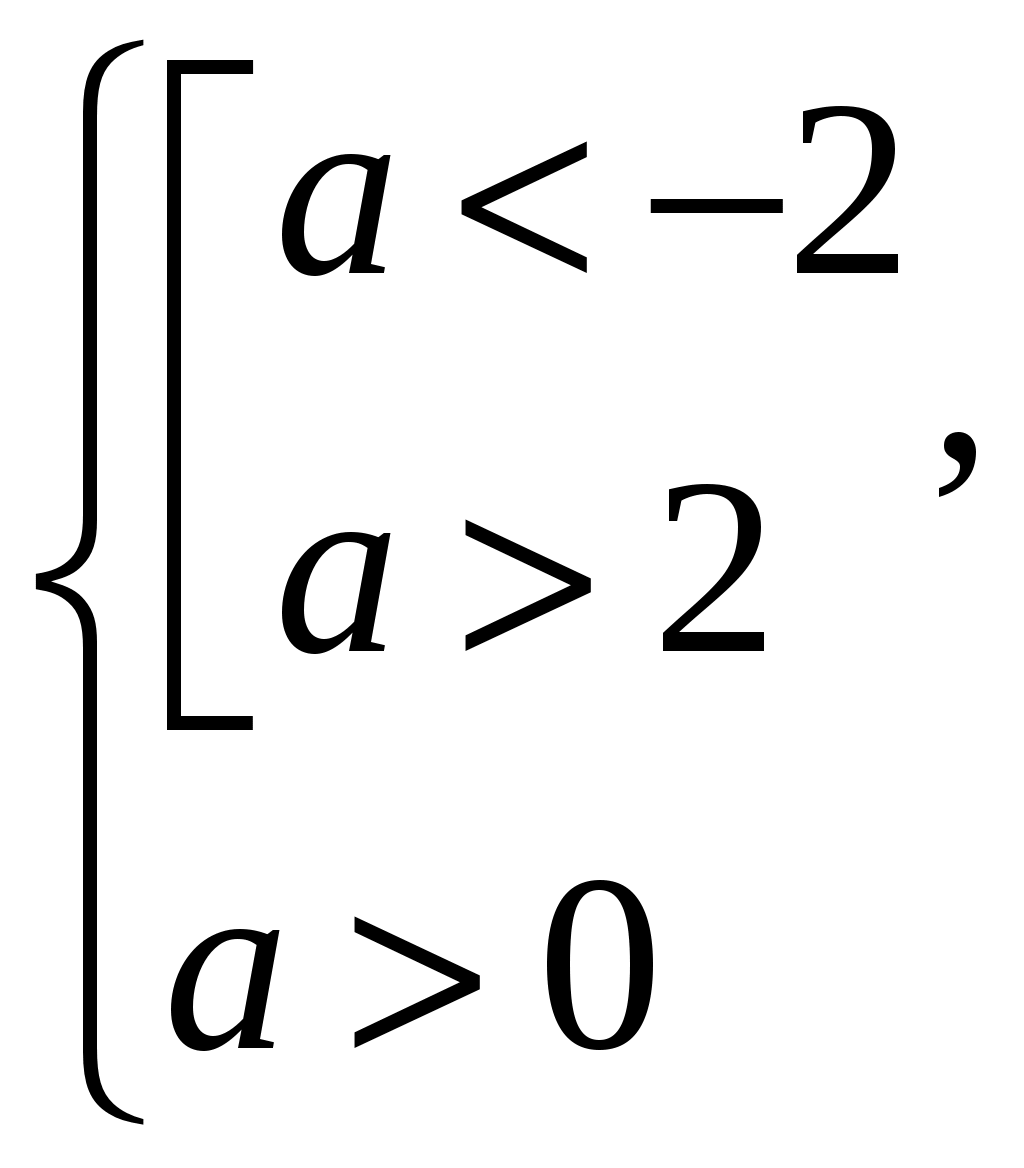 a>2.
a>2.Ответ: a>2.
64. При каких значениях параметра a уравнение ax2 4x+a=0 имеет:
а) положительные корни;
б) отрицательные корни;
в) корень, равный нулю?
Ответ: а) 0 2; б) 2 a<0; в) a=0.
65. В уравнении x2+ax+12=0 определить a таким образом, чтобы разность корней равнялась единице.
Решение: x2 x1=
Ответ: a= 7.
Разнообразны задачи с применением формул сокращенного умножения.
66. Корниуравнения x2 3ax+a2=0 таковы, что x1 2+ x2 2=112. Найти a.
Решение:
D=9a2 4a2=5a2, D 0 при любых a.
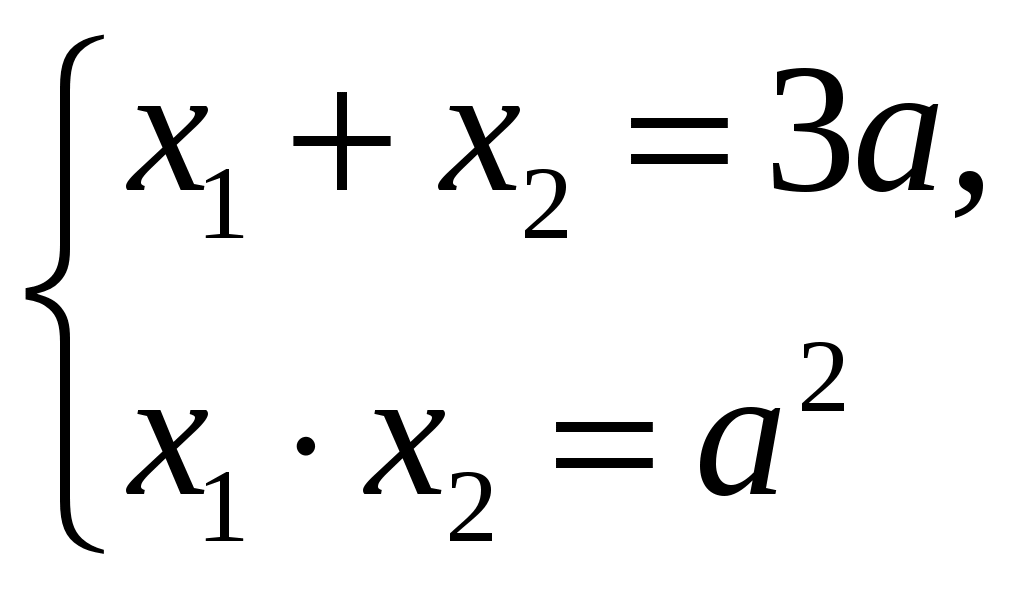 ,
,x12+ x22=(x1+x2)2 2x1 x2=(3a)2 2a2=7a2=112; a2=16, a= 4.
Ответ: 4.
67. В уравнении 3x2+ax+2=0 определить a таким образом, чтобы корни уравнения были действительными, а сумма кубов корней равнялась удвоенной сумме корней.
Решение:
D>0, D=a2 24;
a2 24>0, a2>24; a>2
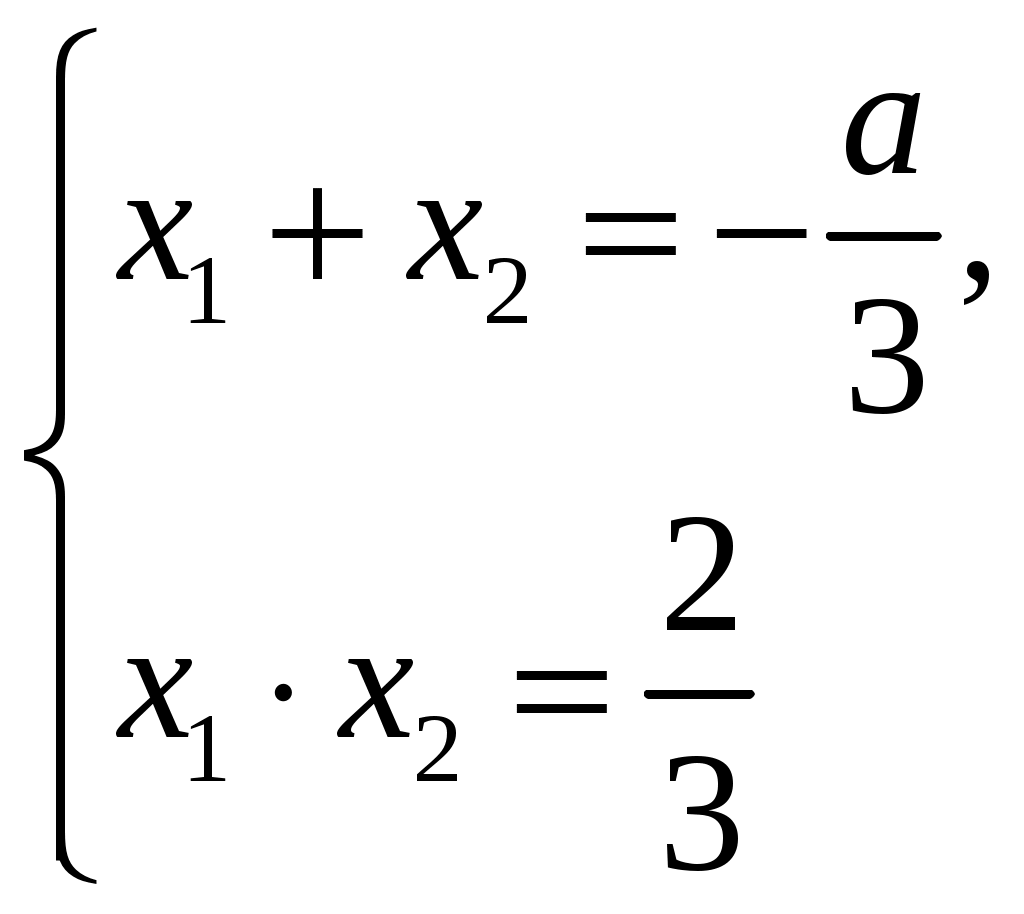
x13+x23=(x1+x2)(x12+ x22 x1 x2)=(x1+x2)((x1+ x2)2 3x1 x2)=
0<2
Ответ: 6.
68. Пусть x1 и x2-корниуравнения x2+px+q=0. Выразить x14+ x24 через p и q.
Решение:
1)x1+x2= p;
x1 x2=q.
2) x14+x24=(x12+ x22)22x12x22=((x1+x2)22x1x2)22x12x22=(p2-2q2)2-2q2=
=p4-4p2q2+2q2.
Ответ: p4-4p2q2+2q2.
69. При каком значении параметра m сумма квадратов корней уравнения x2+(m 1)x+m2 1,5=0 наибольшая?
Ответ: –1.
70. При каком значении параметра m сумма квадратов корней уравнения x2+(2 m)x+m 3=0 наименьшая?
Ответ: 1.
Учащиеся должны самостоятельно уметь решать задачи типа 59, 62, 65. Задачи такого типа целесообразно включать как обязательный материал в текущие самостоятельные и контрольные работы.
Итоги работы за год покажет большая проверочная работа, в которую включены задачи, аналогичные ключевым по всем темам.
9 класс
Основная цель работы в 9 классе – просто изучить квадратный трехчлен и квадратные неравенства. Учащиеся 9 класса уже готовы к серьезной исследовательской работе, поэтому излагать новый материал можно в виде проблемного диалога между учениками и учителем.
Квадратичная функция и ее график
При изучении графиков функций y=ax2+nиy=a(x-m)2 в устную и письменную работу полезно включать задачи такого содержания.
71. Найдите количество целых значений а, при которых абсцисса и ордината вершины параболы y=(x-5-a)2+3-a положительны.
Решение: y=(x-(5+a))2+3-a; х0=5+а; y0=3-a.
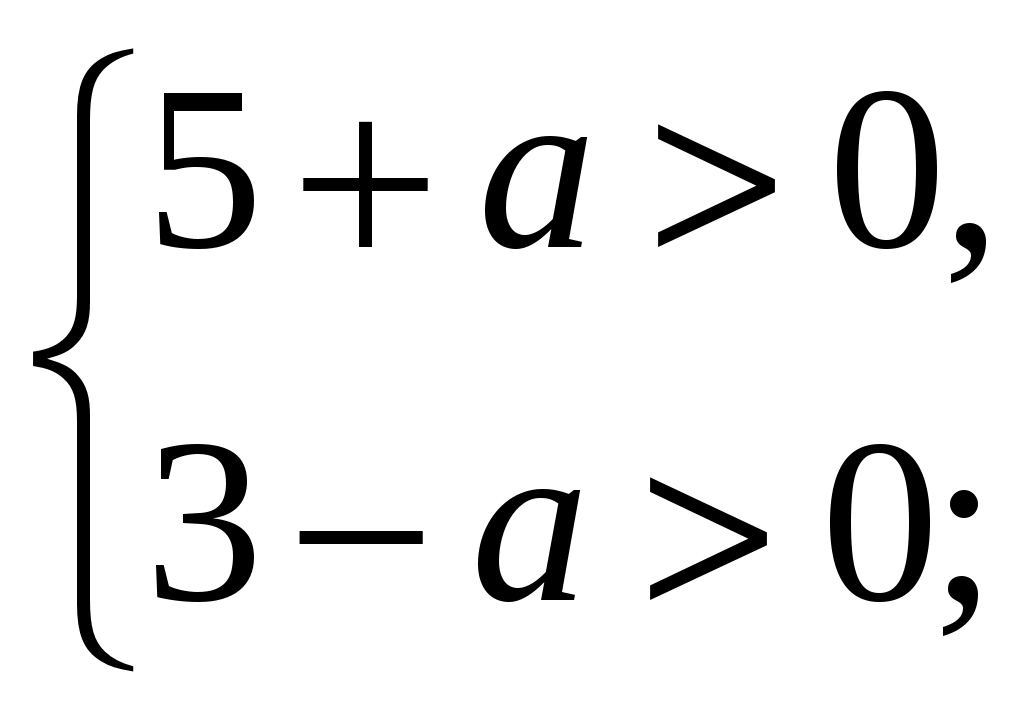
 –5<а<3.
–5<а<3.Целые значения а: –4; –3; –2; –1; 0; 1; 2.
Ответ: 7.
Изучая график квадратного трехчлена, рассматриваем следующие задачи:
72. При каких m парабола y=mx2-4mх+35 касается оси абсцисс?
Решение: Парабола касается оси абсцисс, если дискриминант равен 0
D1=(2m)2-m35=4m2-35m=4m (m-
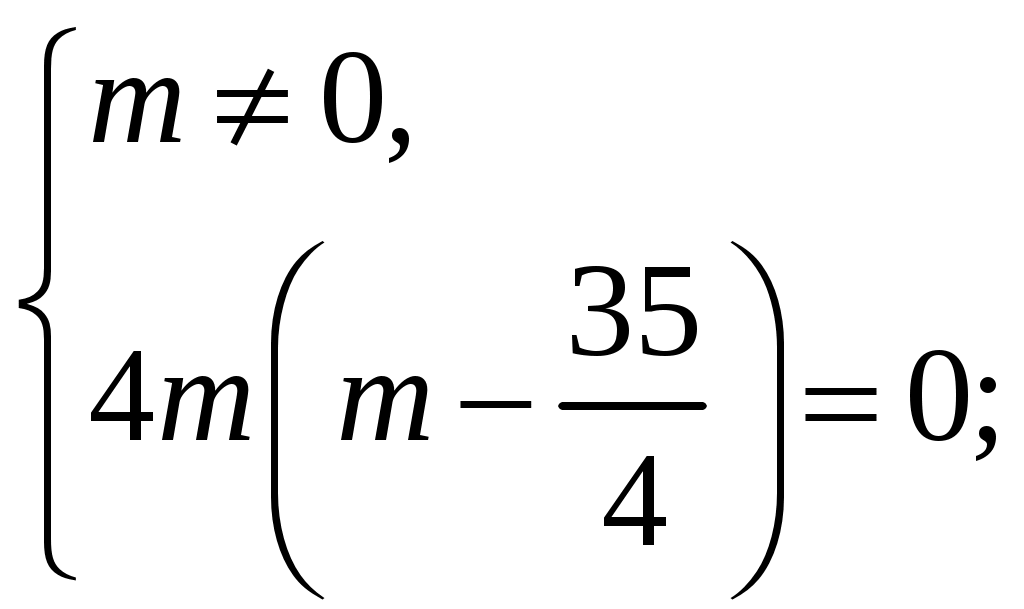
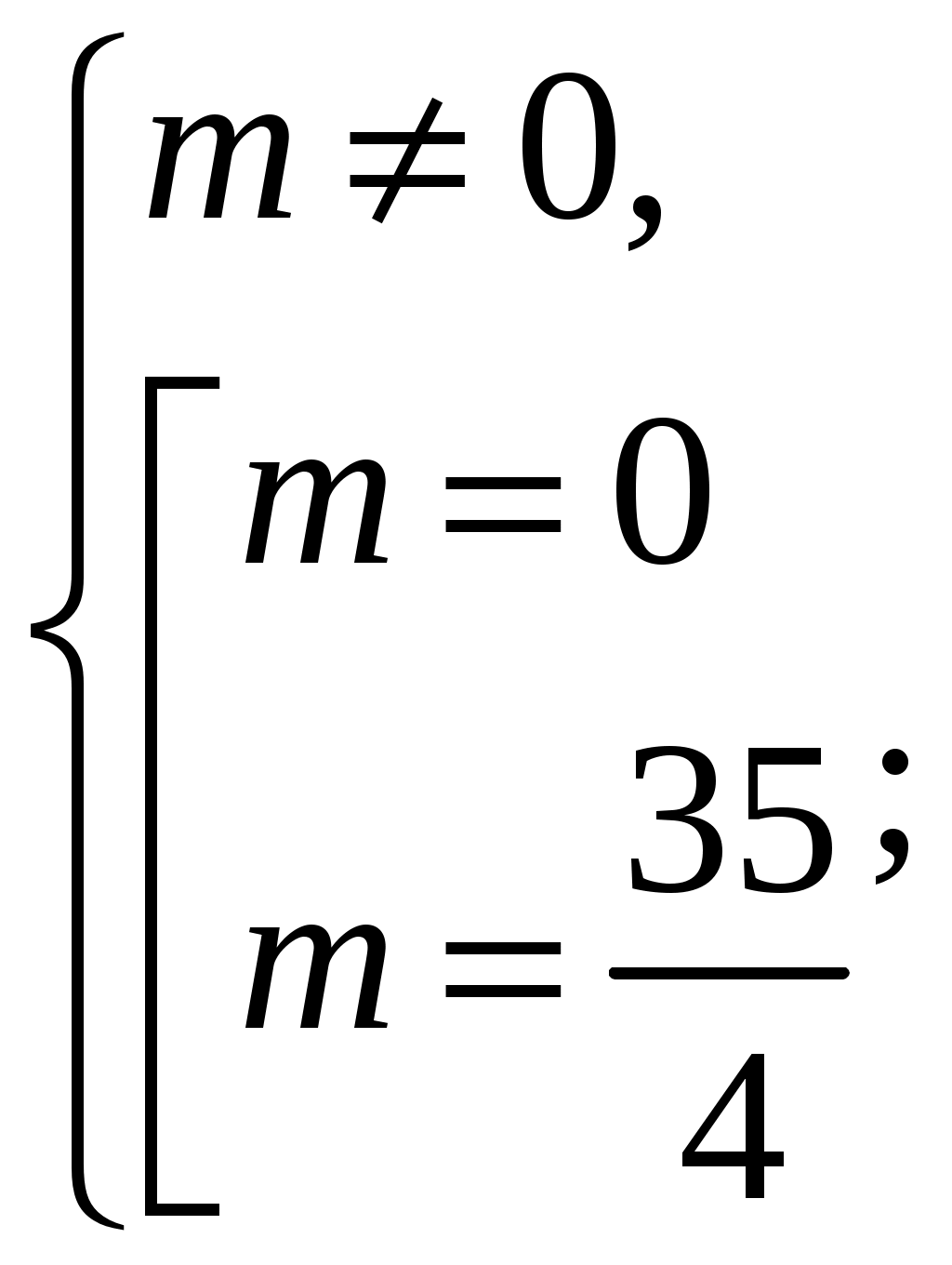
Ответ:
Замечание. При решении таких задач следует всякий раз акцентировать внимание на том факте, что значение первого коэффициента не должно обращаться в ноль.
73. Найдите значения а и b, при которых точка (1; 1) является вершиной параболы
y=аx2+bх+8.
Решение: Если точка (х0; y0)-вершина параболы, то х0=–
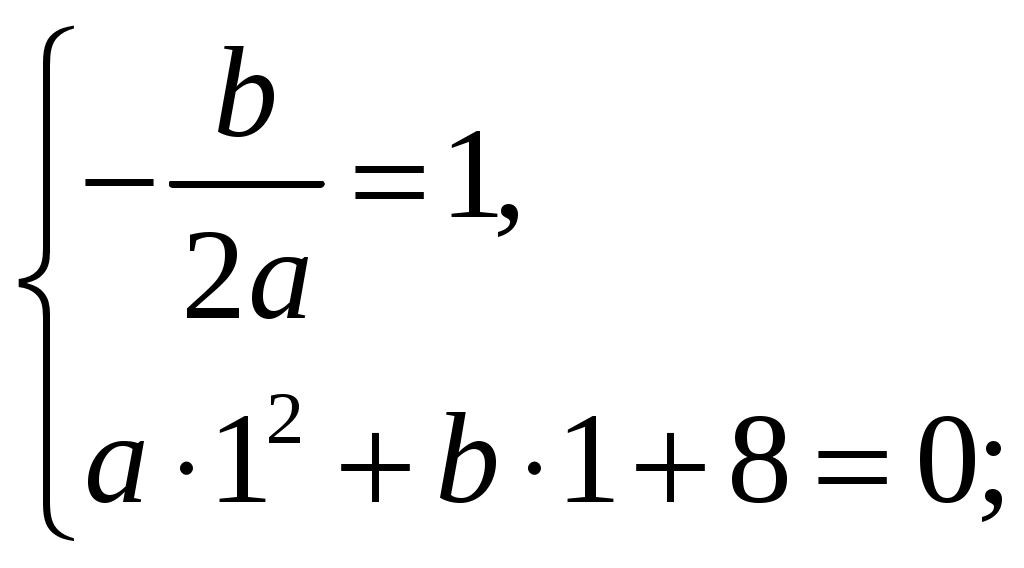
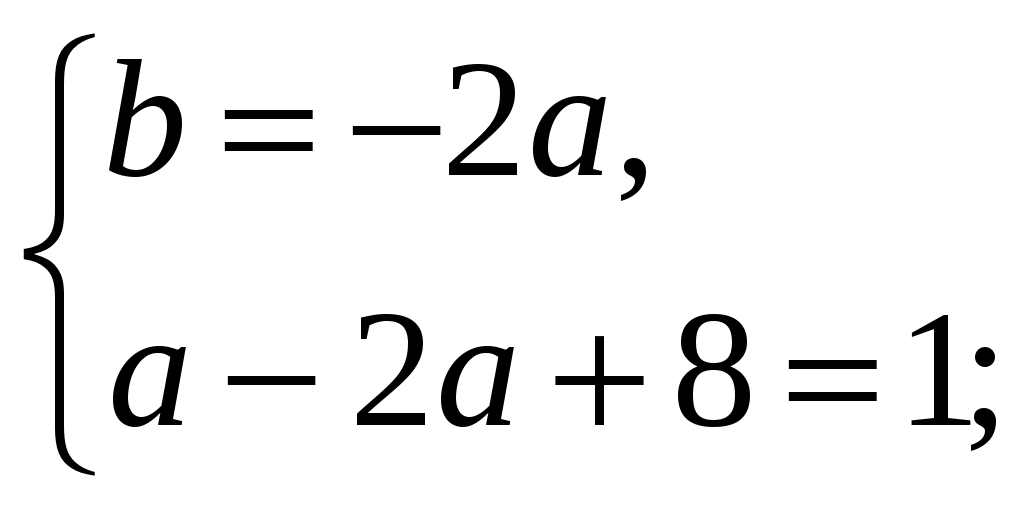
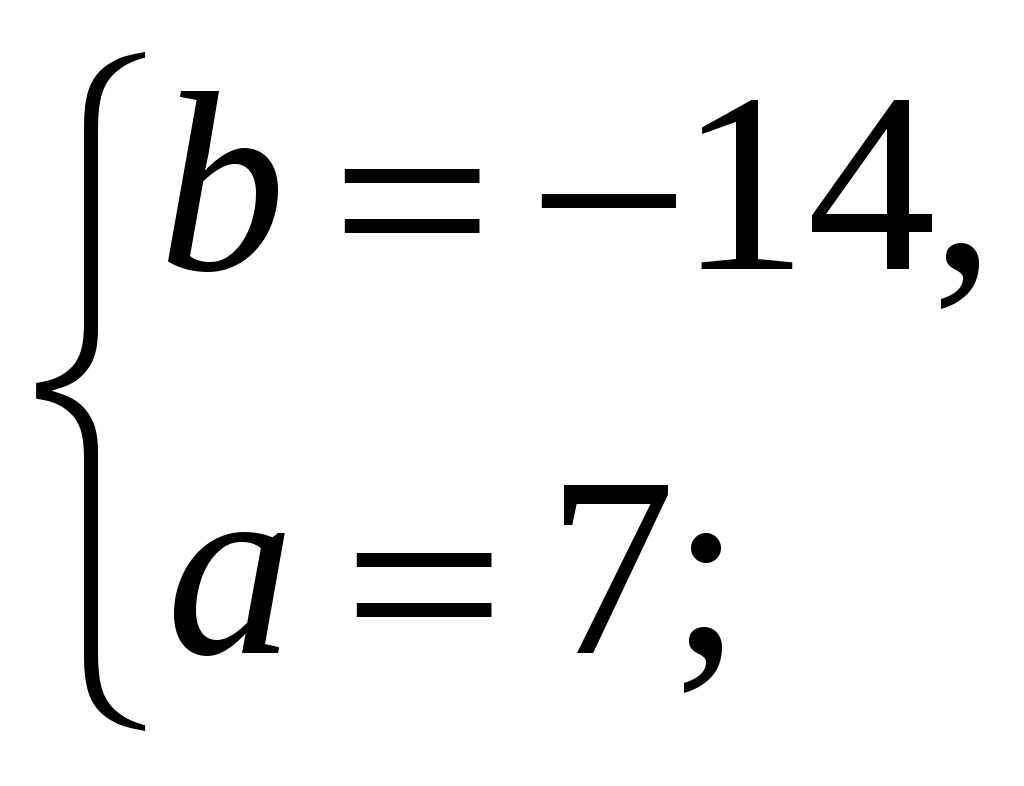
Ответ: а=7; b=–14.
Очень содержательными, по-настоящему развивающими исследователь-ские навыки являются задачи типа:
74. Известно, что парабола y=аx2+bх+с не пересекает ось 0х и a+b+ c< 0. Определить знаки а и с.
Прежде, чем записать решение задачи, рассмотрим утверждения:
1. Если парабола не пересекает ось 0х, то она полностью лежит или над осью, или под осью, то есть при всех х принимает значения одного знака.
2. Значение функции при х=0 равно ее свободному члену, т.е. y(0)=c.
3. Значение функции при х=1 равно сумме коэффициентов y(1)=a+b+c.
Решение:
1) y(1)=a+b+c. Так как a+b+c<0, то y(1)<0.
2) Функция принимает значения одного знака, следовательноy<0 при всех х, т. е. парабола лежит под осью 0х, таким образом а<0,y(0)<0, с<0.
Ответ: а<0; с<0.
75. Квадратный трехчлен аx2+bх+с не имеет корней, а его коэффициенты связаны условием ab+c<0. Определить знак числа с.
Решение:
D<0, следовательно y>0 или y<0 для всех х.
y()=ab+c. Так как ab+c<0, то y()<0, таким образом y<0 для всех х.
с=y(0); y(0)<0, значит с<0.
Ответ: с<0.
76. Известно, что квадратное уравнение аx2+bх+с=0 не имеет корней и a+c<
b. Определить знак с.
Решение: совпадает с решением задачи 76.
Ответ: с<0.
Пока девятиклассники не научились решать квадратные неравенства, им предлагаются задачи простые по технике решения. Важно, чтобы ученики могли грамотно проанализировать условие и вопрос задачи и правильно составить соответствующую систему.
Квадратные неравенства
Решение квадратных неравенств с параметрами – один из наиболее сложных вопросов 9 класса. Задачи очень разнообразны по формулировкам и порой достаточно трудоемки, объемны по записи решения, поэтому уже на первых уроках изучения темы "Решение неравенств второй степени с одной переменной" ученики составляют в тетради таблицу, которой активно пользуются сначала при решении числовых неравенств, а потом и неравенств с параметрами.
Изучив графический способ решения квадратных неравенств и рассмотрев примеры всех возможных типов, девятиклассники делают вывод, что возможны шесть случаев положения параболы относительно оси 0х. Факторы, влияющие на положение параболы-знак первого коэффициента и знак дискриминанта. Исследуем решение всех случаев.
Решение квадратных неравенств
f (x)>0(x)=Ax2+Bx+C, где А, В, С – некоторые числа или выражения,
зависящие только от параметра, причем А 0, х1 , х2-нули функции.
| A, D | Эскиз графика | f(x)>0 | f(x) 0 | f(x)<0 | f(x) 0 |
| A>0 D>0 | 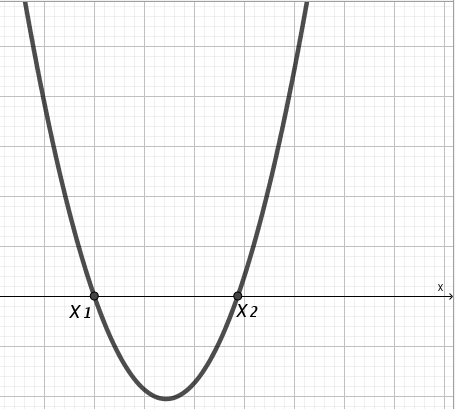 | (–;х1)U(х2;+) | (–;х1]U[х2;+) | (х1; х2) | [х1; х2] |
| A>0 D=0 | 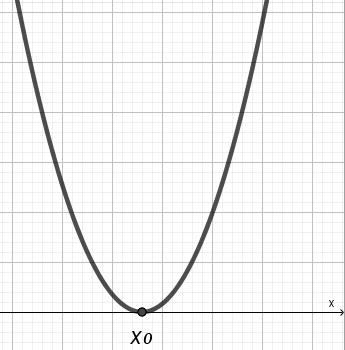 | (–;х0)U(х0;+) | (–; +) | решений нет | х0 |
| A>0 D<0 |  | R знак значений функции совпадает со знаком а | R | решений нет | решений нет |
| A<0 D>0 |  | (х1; х2) | [х1; х2] | (–;х1)U(х2;+) | (–;х1]U[х2;+) |
| A<0 D=0 |  | решений нет | х0 | (–;х0)U(х0;+) | R |
| A<0 D<0 |  | решений нет | решений нет | R знак значений функции совпадает со знаком а | R |