Файл: Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc
Добавлен: 09.11.2023
Просмотров: 175
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В первую очередь ученикам предлагаются неравенства, которые должны выполняться или не выполняться при всех действительных значениях х.
77. При каких значениях а неравенство x2(а+2)х+8а+1>0 выполняется для всех действительных значений х?
Решение: Неравенство выполняется для всех х, если имеет решение система
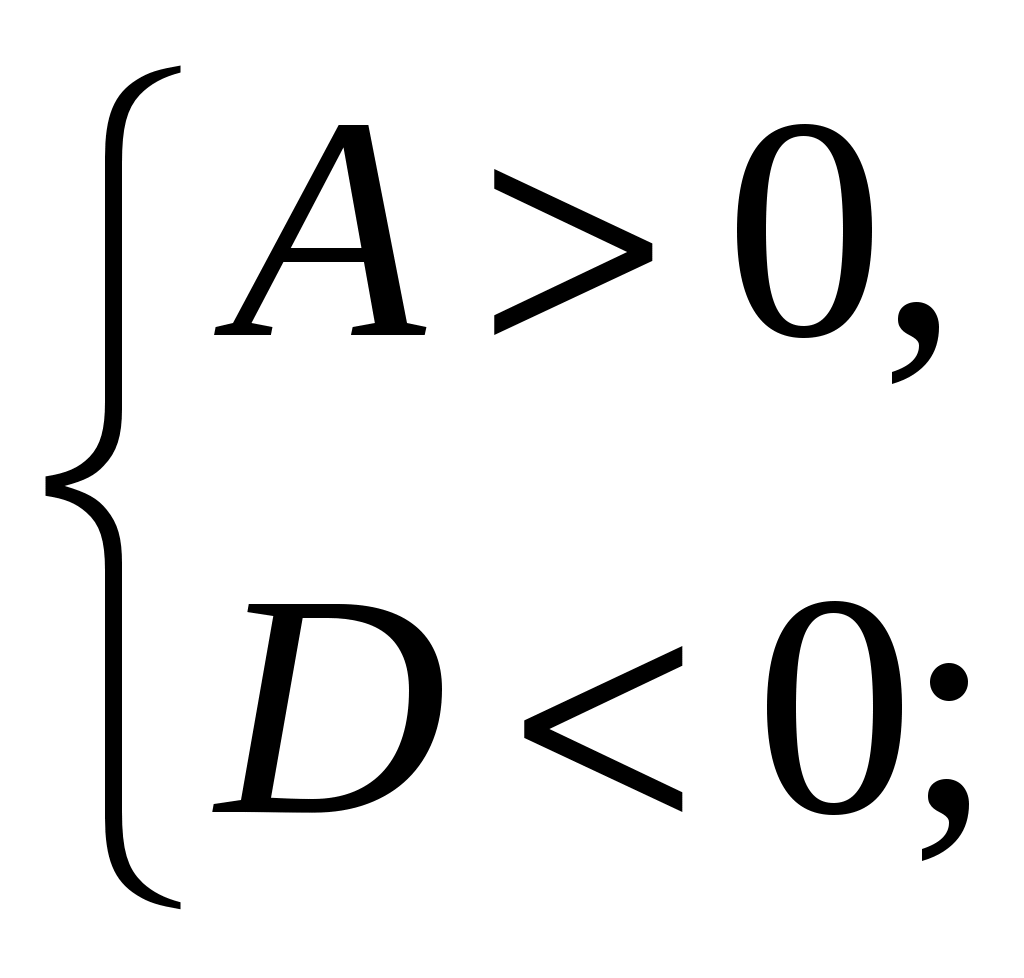
1) А=1; 1>0.
2) D=(а+2)2+4(8a+1)=а2+4а+4 32а 4=а2 28а=а(а 28).
3
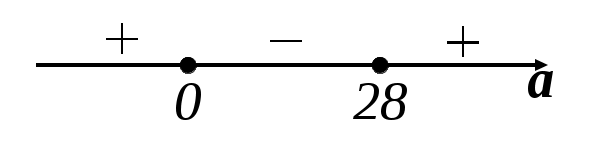) а(а 28)<00<а<28.
Ответ: (0; 28).
78. При каких значениях b квадратное неравенство (4 b)x2+2(b+2) х 1>0 не имеет решений?
При разборе условия задачи ставим акцент на слове "квадратное". Обращаемся к таблице, находим в ней соответствующий случай. Выясняем, что имеется два случая: 1) А<0, D =0;2) А<0, D< 0, которые можно объединить.
Решение: Неравенство не имеет решений, если имеет решение система
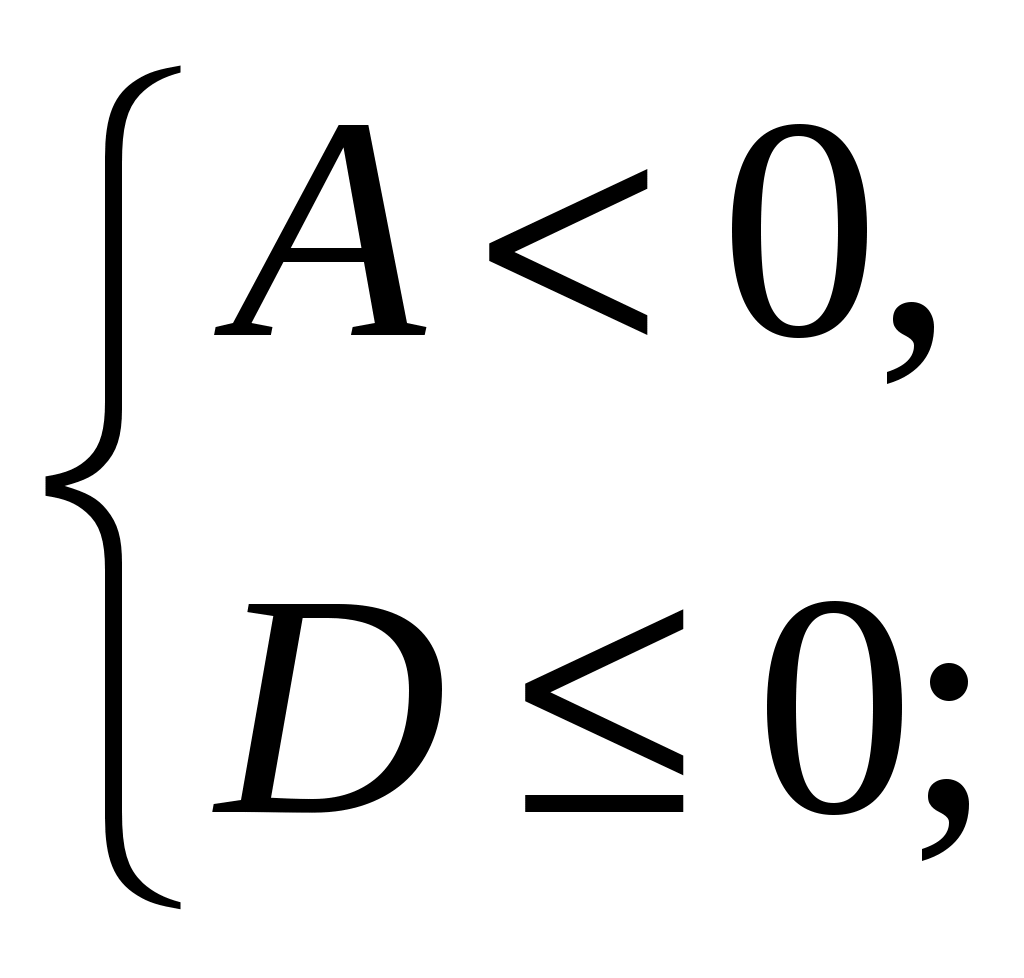
1) А=4 b2.
2
3
) 
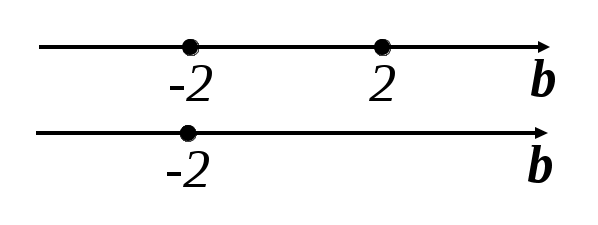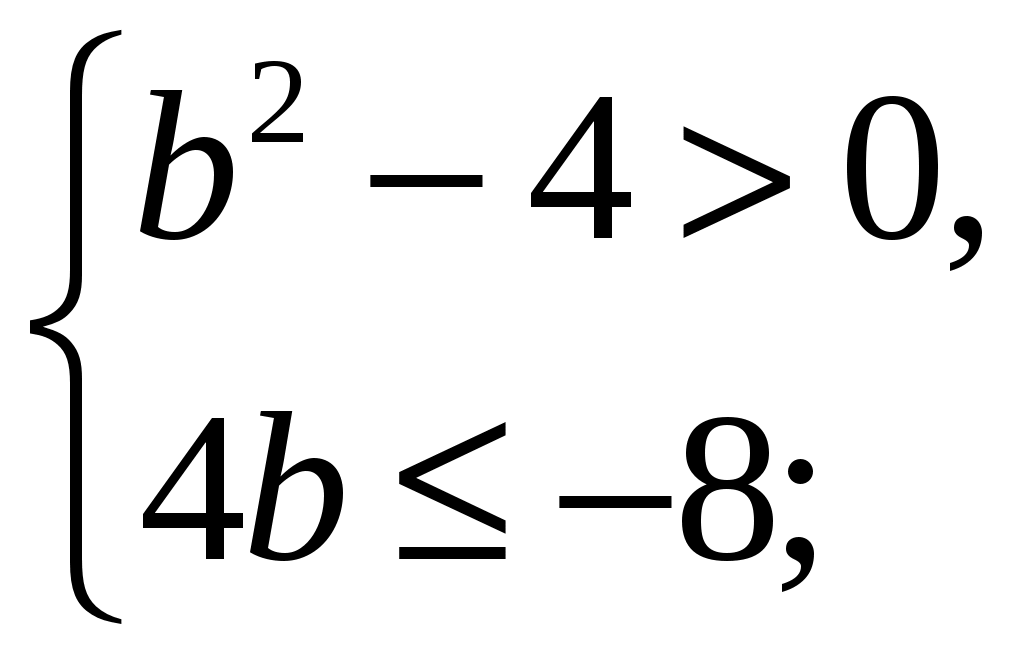
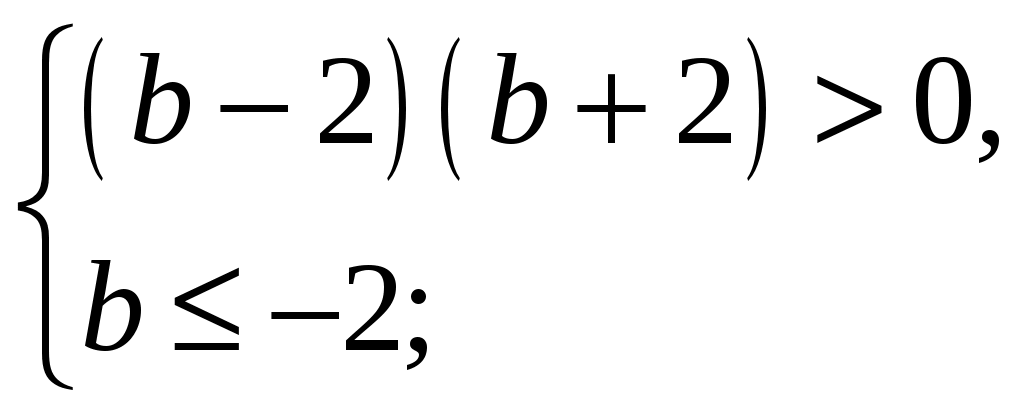
b<-2
Ответ: (; 2).
Перед тем, как рассматривать следующую группу задач, полезно обсудить с учениками упражнение:
При каких значениях а уравнение ах2х+3=0 имеет единственное решение?
Вспомнить, что при изменении параметра могут измениться и важнейшие характеристики уравнения.
79. Найти все значения r, при которых неравенство (r2 1)х2+2(r 1)x+2>0 является верным при всех х R.
При обсуждении выражения, стоящего в левой части, говорим, что при некоторых значениях rнеравенство будет линейным.
Решение:
1) r21=0 при r=1.
а) если r=1, то 4x+2>0, x<0,5, не удовлетворяет условию х R.
б) если r=1, то 0x>2, х R.
2) r2 1 0.
Неравенство выполняется для всех х, если имеет решение система
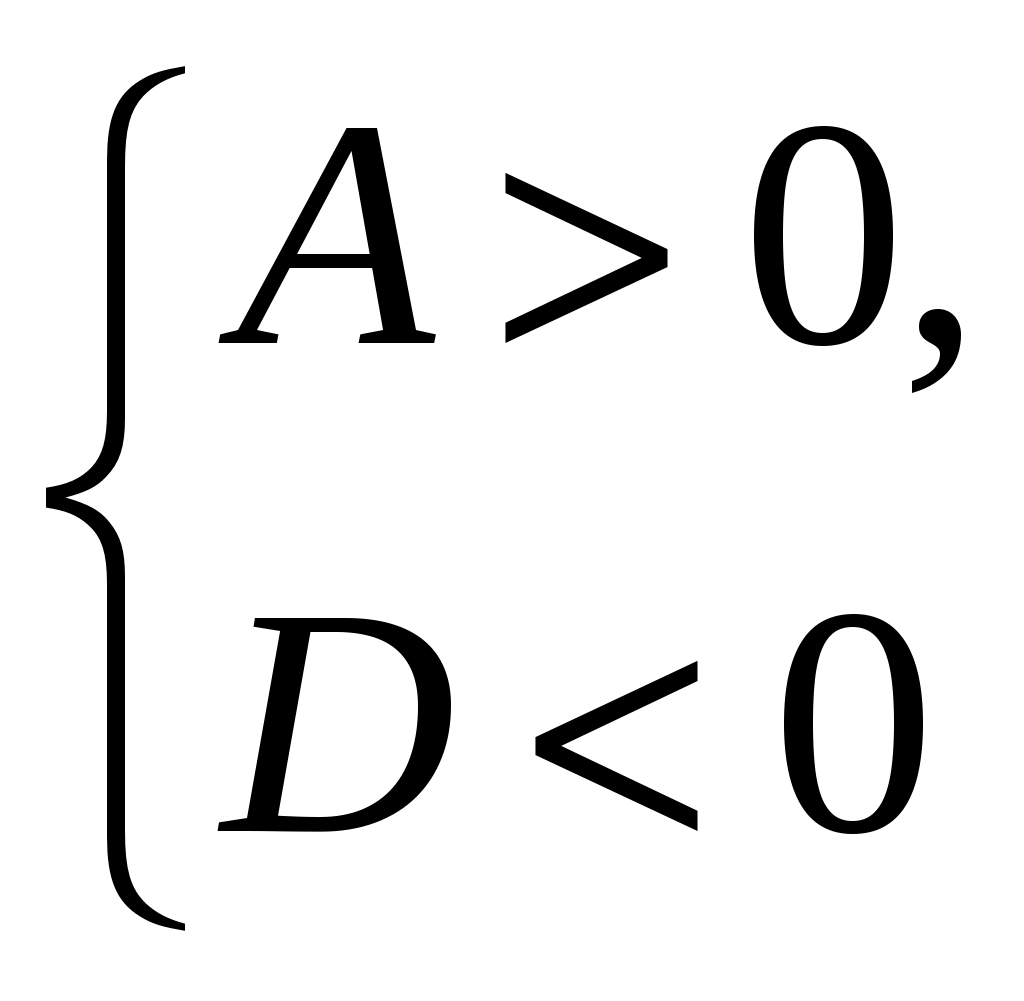
А=r2 1;
D1=(r 1)2 2(r2 1)=(r 1)(r 1 2(r+1))=(r 1)(r 3)
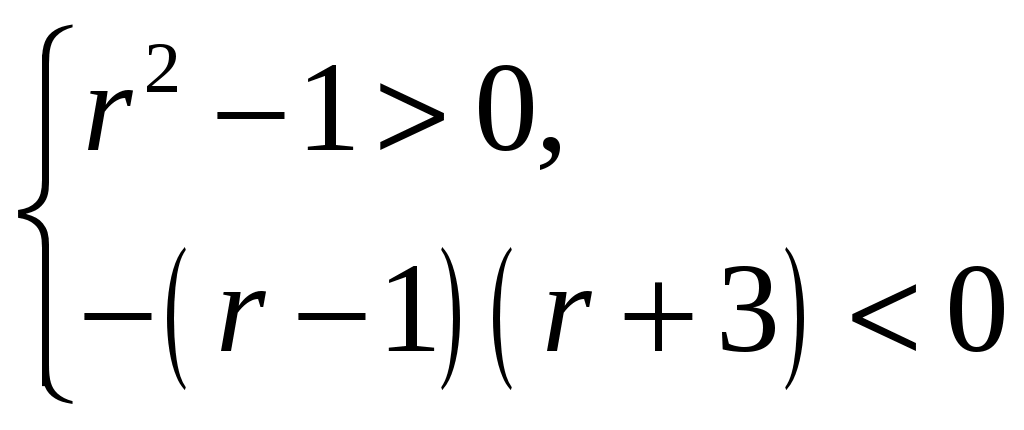
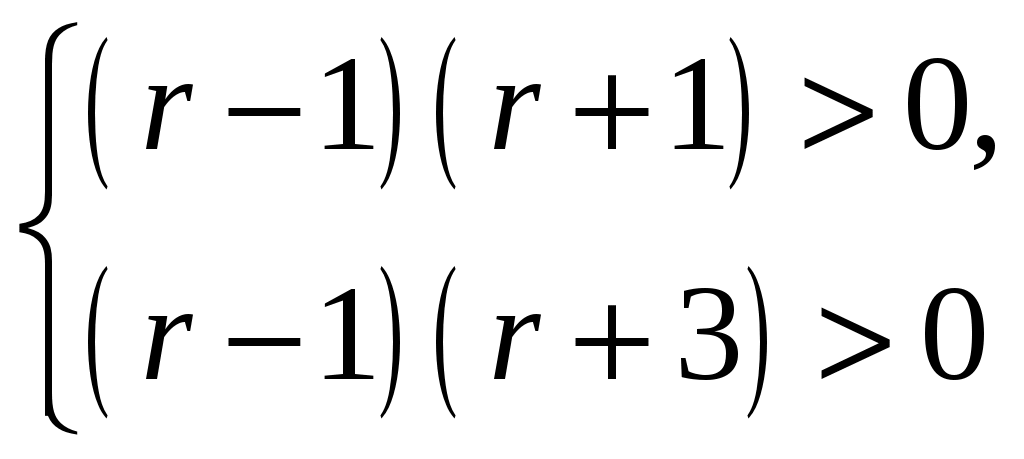
С учетом п. 1 (б)
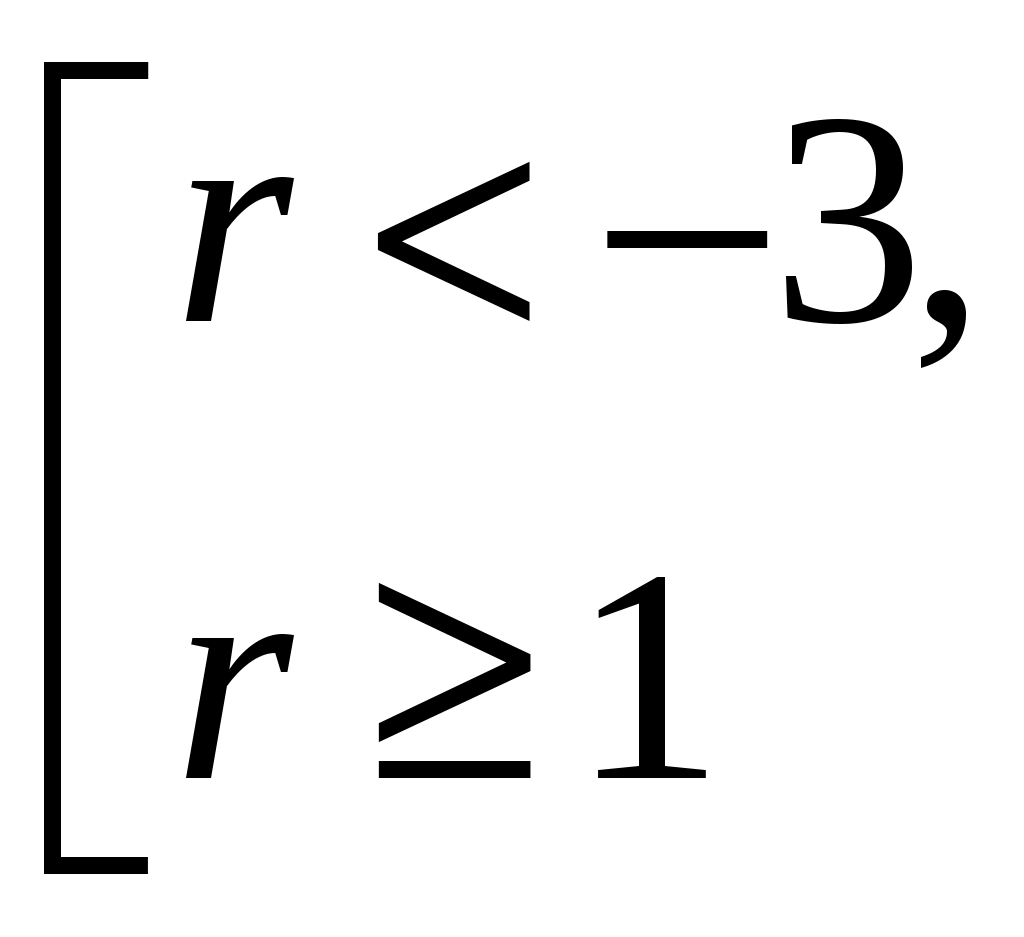
Ответ: (; 3) U[1; +).
Для закрепления решаем задачи:
80. При каких значениях р функция y =
определена при всех действительных значениях х?Решение: px2+(3p+1)x 4p 0;
1) p=0; х 0 не удовлетворяет условию х R.
р 0;
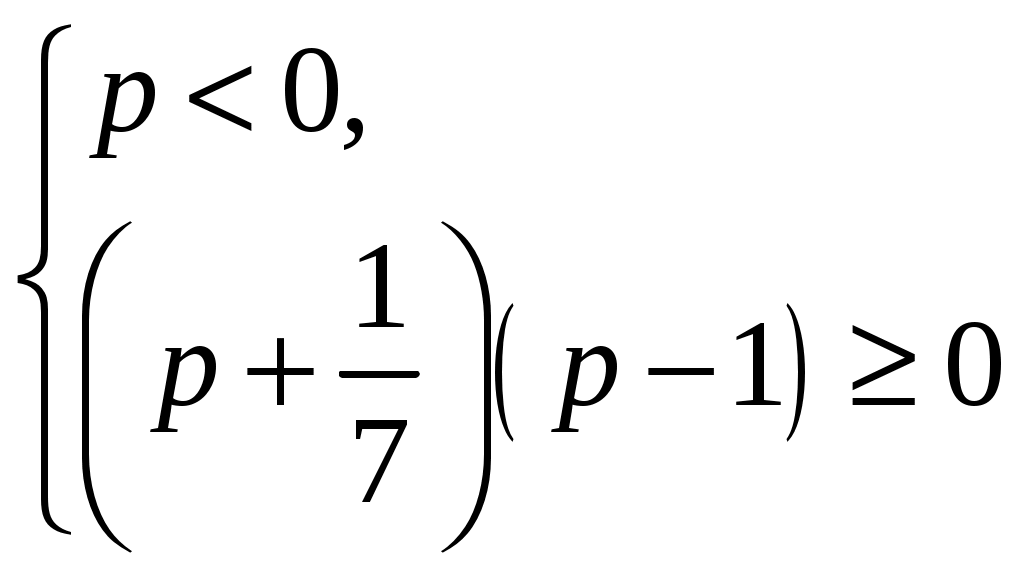
Ответ: (;
].82. При каких mнеравенство (m 1)x2+2mx+3m 2<0 не имеет решений?
Ответ: [2; +).
83. При каких nнеравенство (2n2 5n+2)x2 4nx+2>0 выполняется при всех х?
Ответ: (; 0,4).
84. При каких а квадратный трехчлен (а2 1) x2+2(а 1) x+1 принимает положительные значения для всех х?
Ответ: (1; +).
При работе над этими задачами рекомендую выполнять графическую иллюстрацию, которая зачастую сразу помогает понять суть задачи.
Приступая к решению квадратных неравенств, говорим, что предыдущая группа задачи с дополнительными условиями. Мы искали значения параметров, удовлетворяющих конкретным требованиям.
Если же следует решить неравенство, значит, оно должно быть рассмотрено при всех значениях параметра. Если хотя бы одно значение не исследовано, решение задачи не может быть признано полным. При решении неравенств используем таблицу, чтобы не пропустить все возможные случаи.
В 9 классе достаточно рассмотреть несколько примеров, где первый коэффициент не зависит от параметра.
Решить неравенства:
84. х2+2х+а>0
А=1, А>0;
D1=1 a;
x1=1
; x2=1 + ;1) D1>0; 1a>0; при а<1
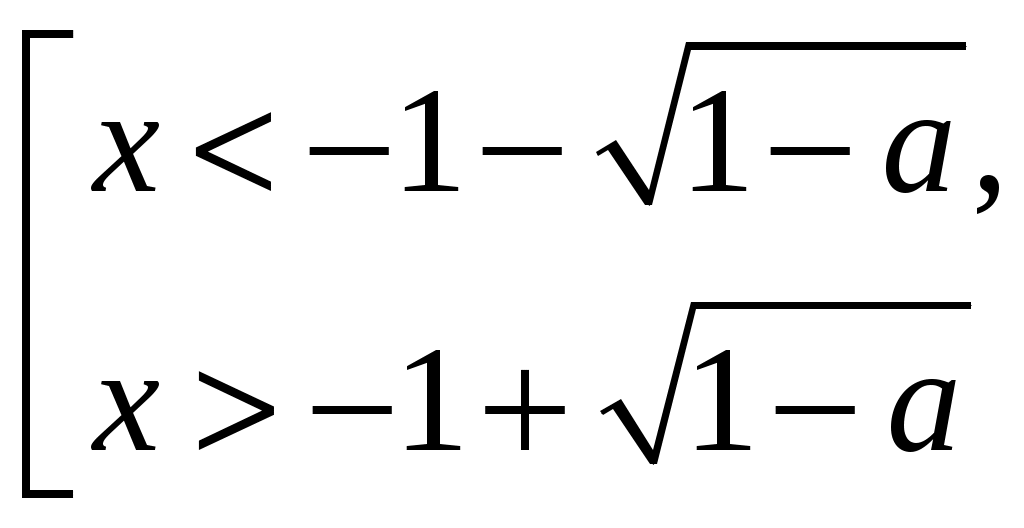
2)D1=0; 1a=0; при а=1 х2+2х+1>0; (х+1)2>0;
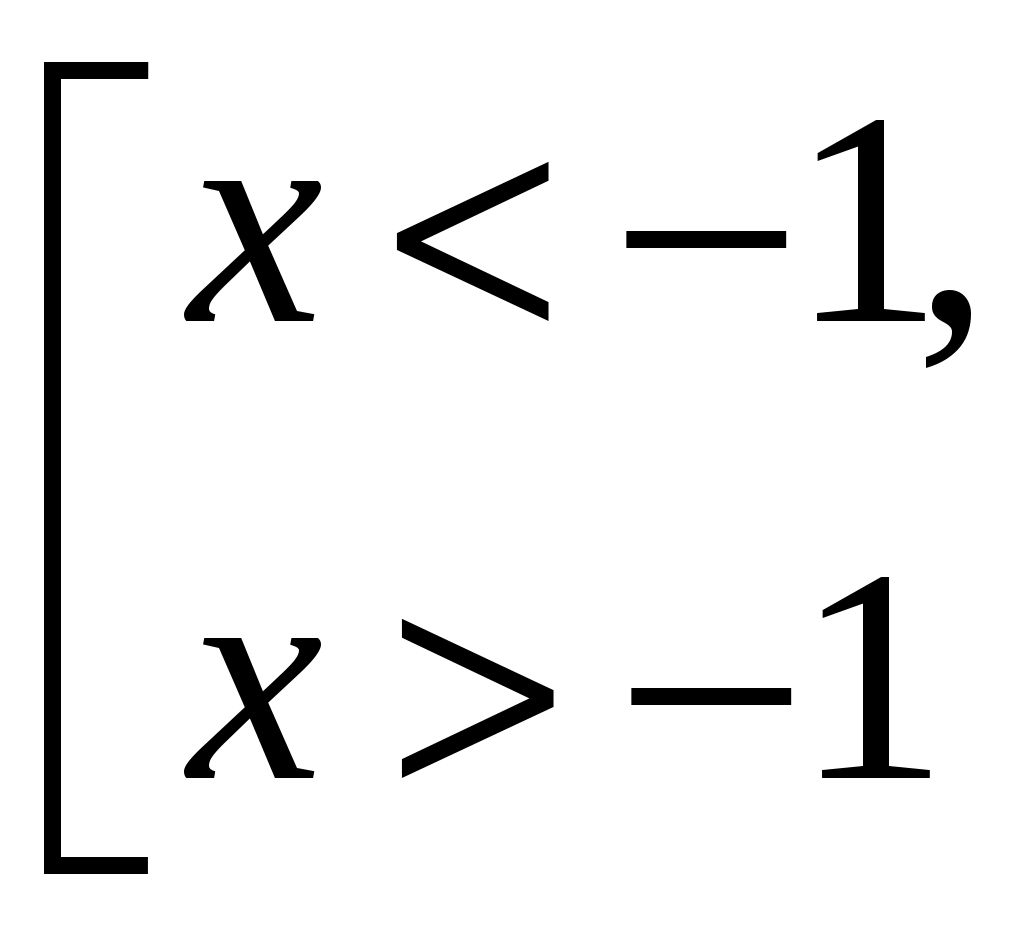
3) D1<0; 1a<0; при а >1 х любое число.
Ответ: при а (; 1) х (; 1
) U (1 + ; +);
при а=1 х (; 1) U (1; +);
при а (1; +) х R.
Аналогичное неравенство:
85. х2+3ах а>0
D=9а (а +
), поэтому следует рассмотреть случаи:1) D>0;
2) D=0; a) а=0; б) а=
;3) D<0.
86. х2 2ах+2а2+4а+4 0
D1= (a+2)2;
1) D>0; (а+2)2>0; таких а нет.
2) D=0 при а=2; х2+4х+4 0; (х+2)2 0; х=2.
3) D<0 при а 2; решений нет.
Ответ: при а=2; х=2;
при а 2 решений нет.
87. х2<ах+1
х2+ах+1>0;
А=1; А>0;
D=а2 4;
х1=
; х2=
;1) D>0; а2 4>0 при
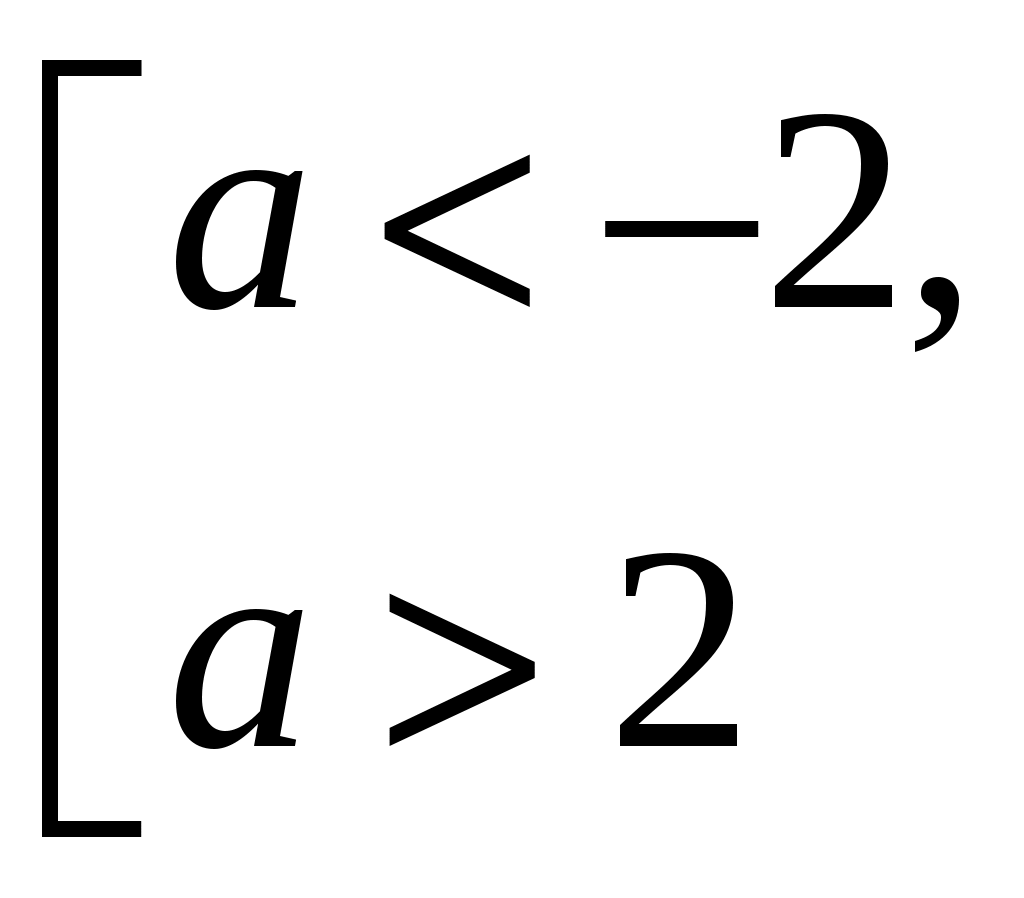х (; х1) U (х2; +).2) D=0; а= 2; а) а=2, (х 1)2>0, х R\{1}
б) а=2, (х+1)2>0, х R\{1}
3) D<0 при 2<а<2, х R.
Ответ: при а <2; х<
или х> ;при а <2; х R;
при а=2; х R\{1};
при а=2; х R\{1}.
Используются различные формы записи решения неравенства, важным является приучить школьников к последовательности в решении и выписке ответа.
Ключевыми задачами этой темы являются задачи 71, 72, 78, 80, 85.
На этапах изучения можно предлагать самостоятельные работы из 1-2 задач, а по завершении темы, учитывая определенную ее сложность домашнюю контрольную работу по ключевым задачам.
1>