Файл: Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc
Добавлен: 09.11.2023
Просмотров: 178
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 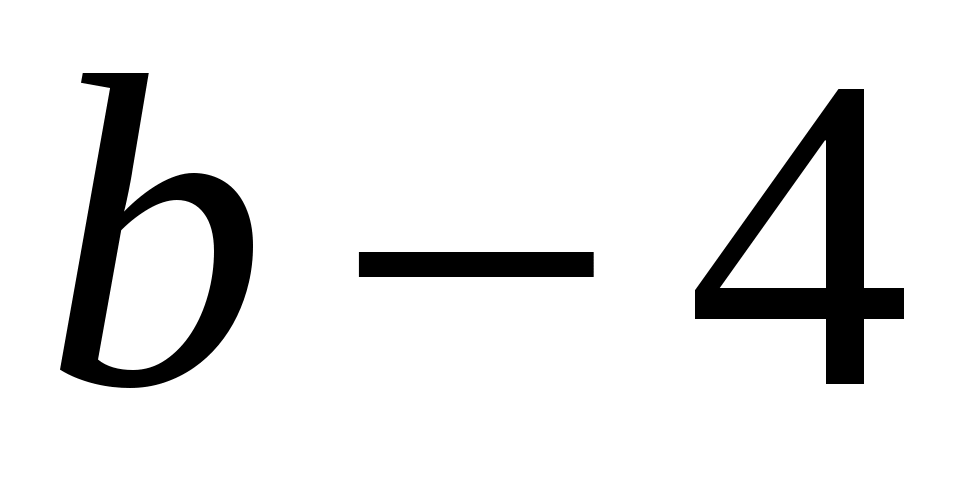 ,
,  , a,
, a, 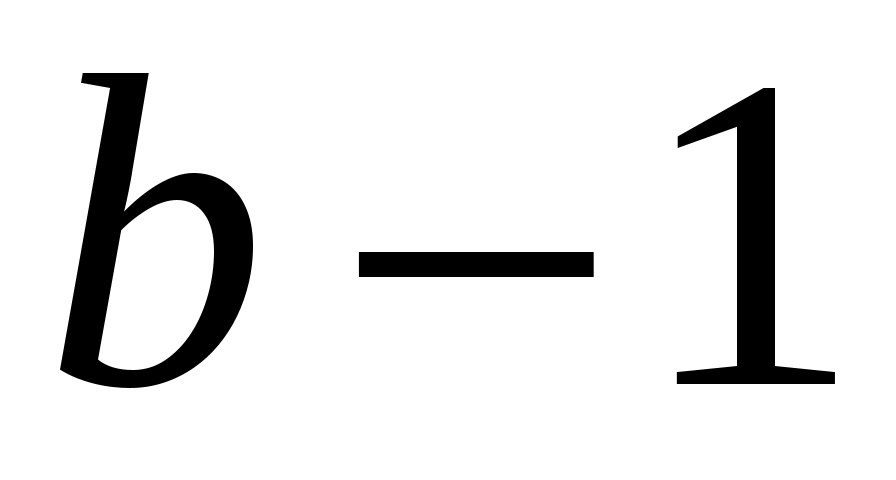 , b.
, b.
Зная, что , сравните числа:
, сравните числа:
а) и b;
и b;
б)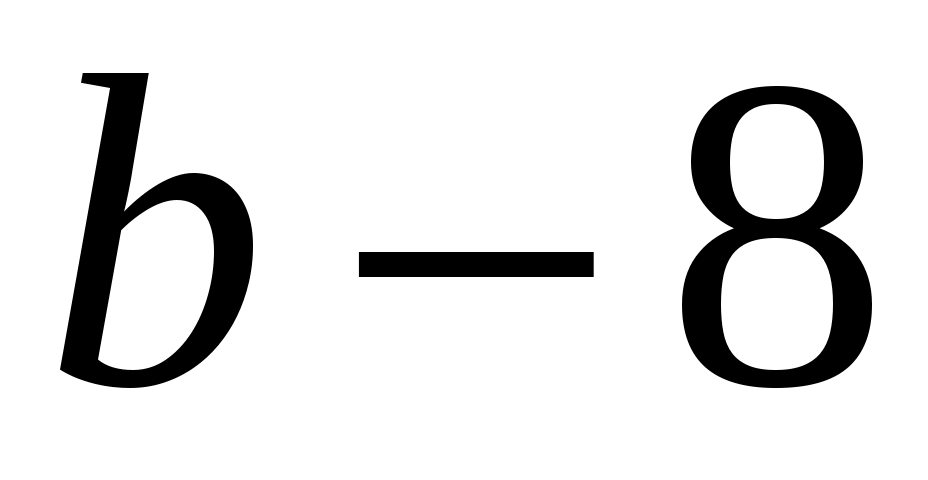 и a;
и a;
в) 12a и 10b;
г) 6a и b.
Очевидно, что данные задания решаются учениками 5 класса интуитивно, так как им не известны свойства неравенств, однако они развивают абстрактное мышление, столь необходимое математику.
Можно попросить проиллюстрировать свое утверждение на конкретных значениях a и b.
1. В каждом ряду зрительного зала m мест, а число рядов на n больше, чем мест в ряду. Сколько мест в зрительном зале?
2. В составе пассажирского поезда 3 мягких вагона и 14 купейных вагонов. В каждом мягком вагоне p мест, а в купейном на q мест больше. Сколько всего мест в таком составе поезда?
3. Запишите число, в котором:
а) 8 десятков и x единиц;
б) xдесятков и 8 единиц;
в) x десятков и y единиц;
г) 5 сотен, x десятков и 4 единицы;
д) x сотен, y десятков, z единиц.
1. При каких значениях a число 5 является корнем уравнения:
а) ;
;
б)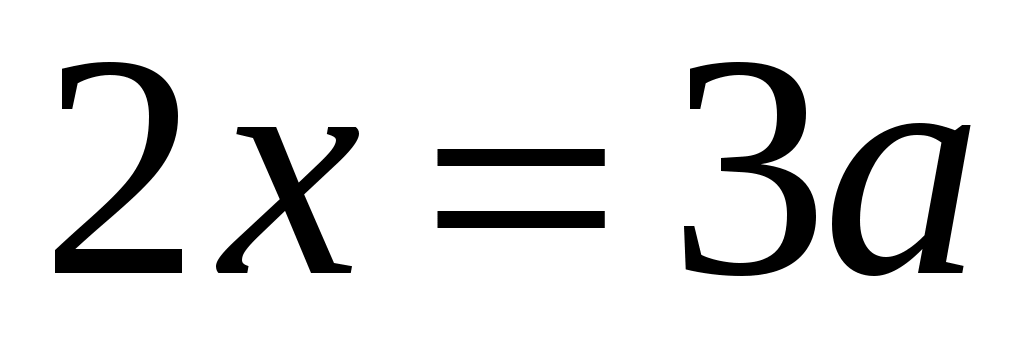 ;
;
в) .
.
2. Какое из двух чисел, обозначенных буквами, больше?
Сравнивая числа в каждом уравнении, докажите, на сколько или во сколько раз больше или меньше:
а)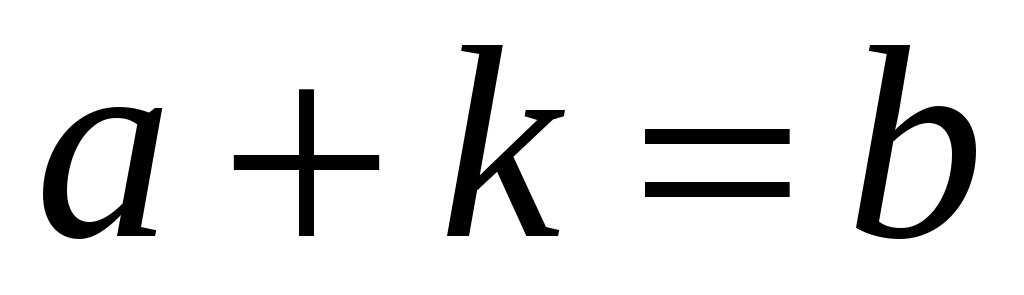 ;
;
б)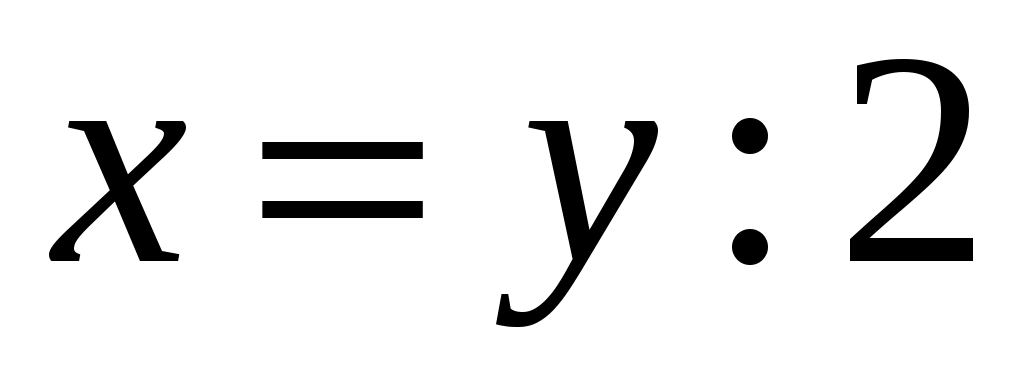 ;
;
в)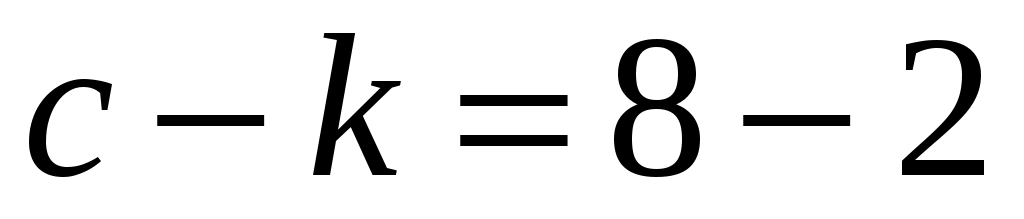 ;
;
г)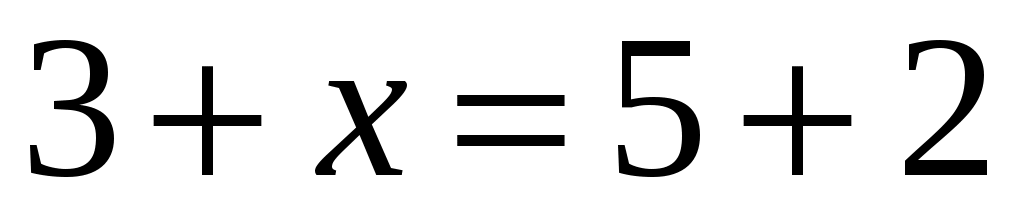 ;
;
д)
;
е) c.
3.Может ли при каком-нибудь значении a быть верным равенство:
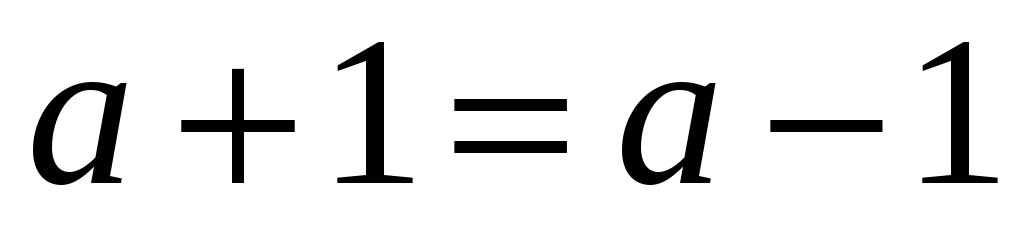 ?
?
1. Составьте формулы для вычисления площадей фигур:
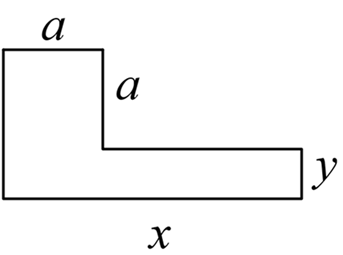
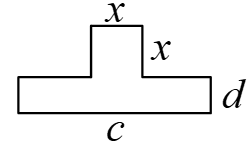 а) б)
а) б)
2. Составьте формулу для вычисления площади заштрихованной части фигуры:
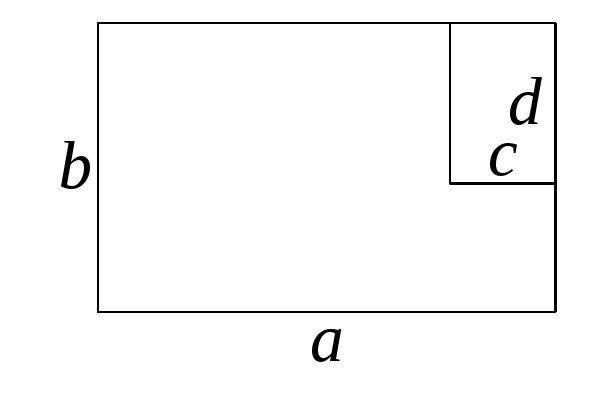
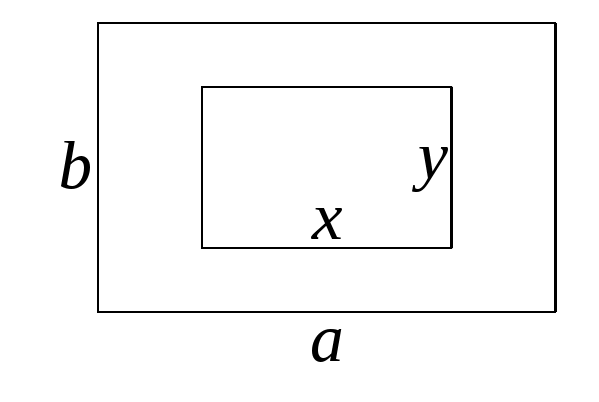 а) б)
а) б)
3. Запишите формулу для вычисления объёма фигуры:

1. Зная, что а>b, сравните числа:
а) aи 8 b; б) (a 4) и b.
2. Известно, что а>b>0. Сравните:
а) 15aи 8b; б) 3a и 2b.
3. Положительным или отрицательным числом является значение выражения
4kmn, где mи n-отрицательные числа?
4. Сравнить: а) a и 3a.
Решение: Следует рассмотреть три случая:
Если a<0, то a>3a.
Если a=0, то a=3a, (0=3 0; 0=0).
Если a>0, то a<3a.
б) a и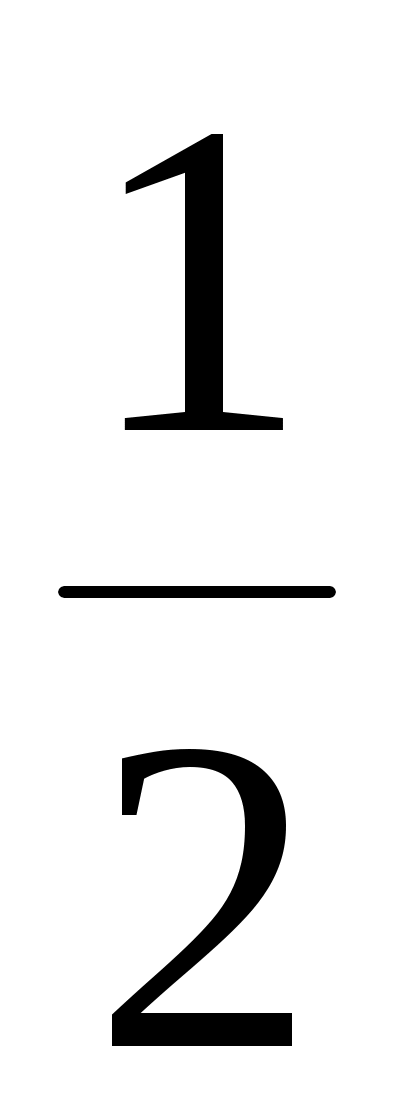 a.
a.
Решение: 1) Если a<0, то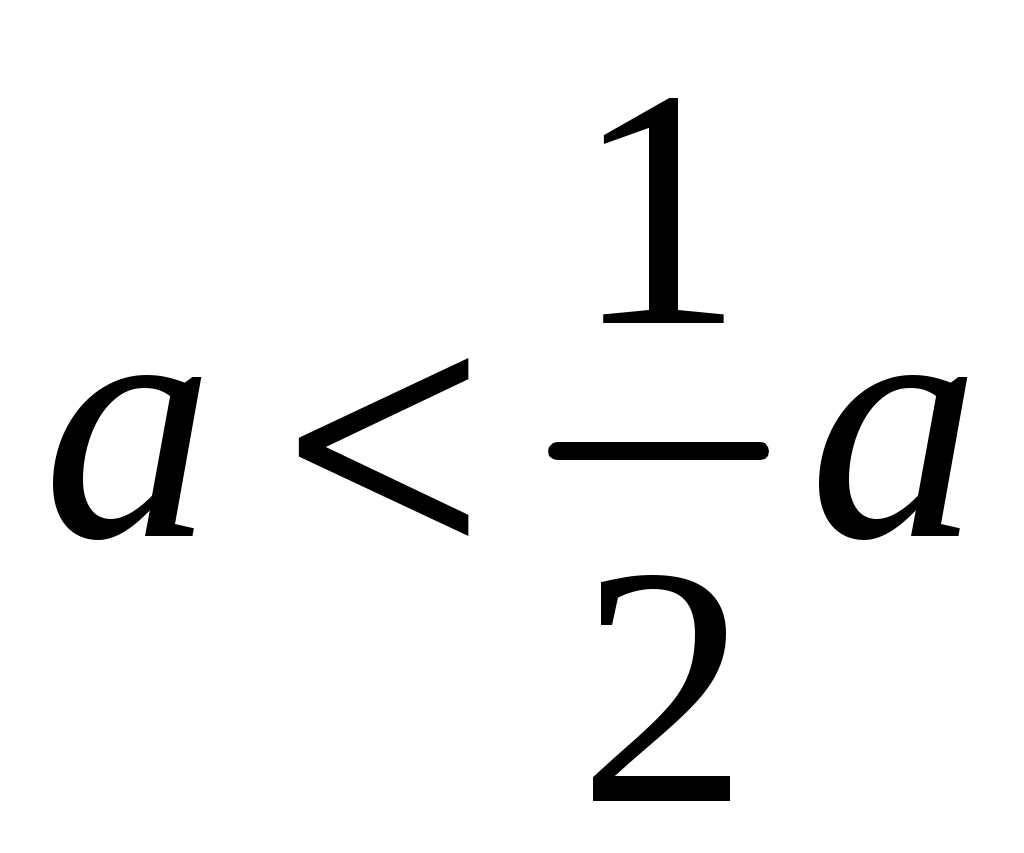 .
.
Если a=0, то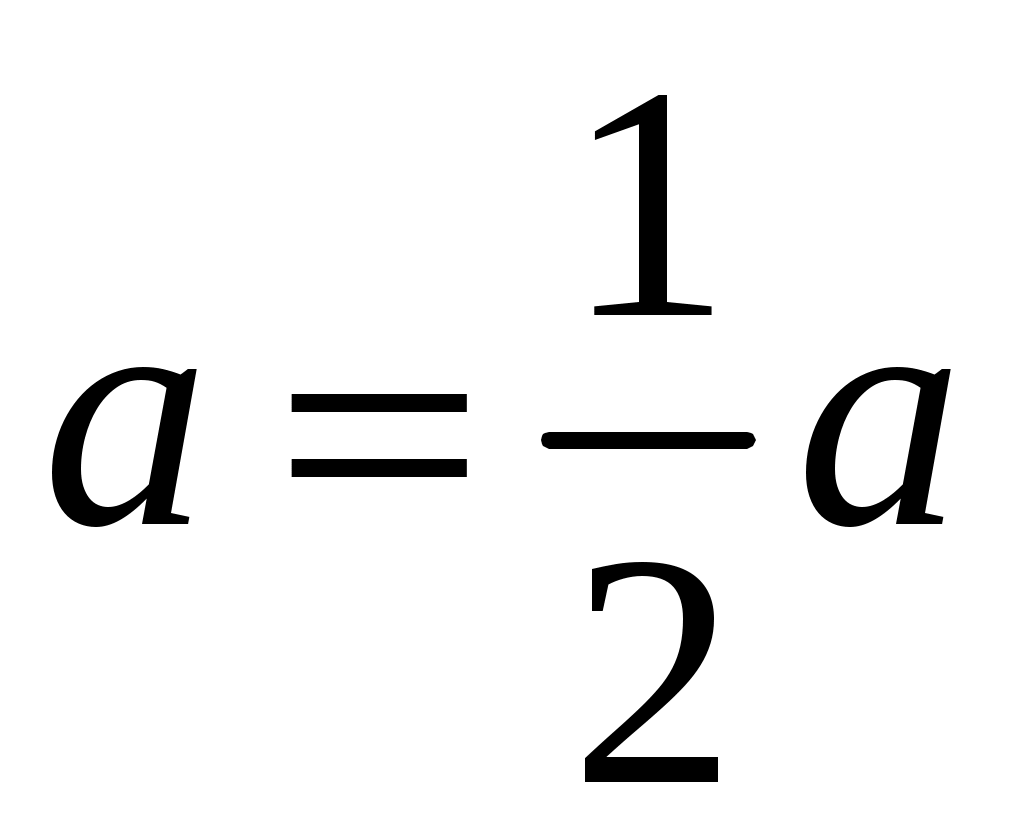 , (
, ( ; 0=0).
; 0=0).
Если a>0, то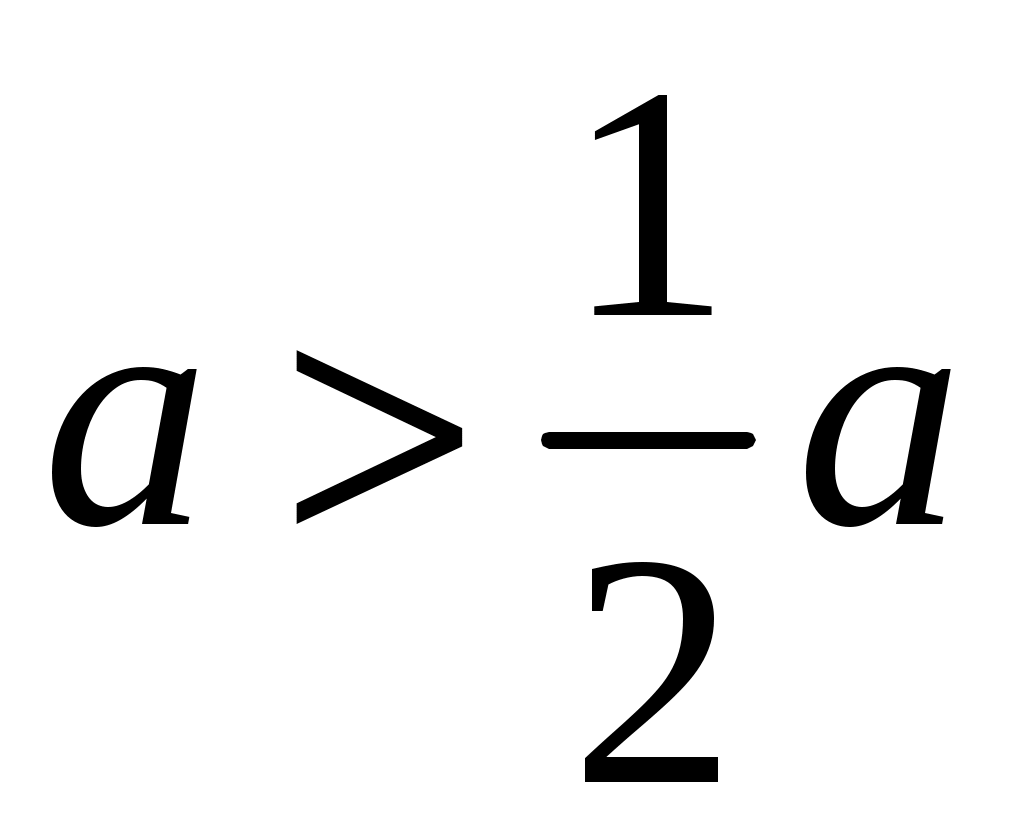 .
.
При решении задач такого рода желательно иллюстрировать рассуждения на координатной прямой.
1. При каких значениях k уравнение kz=8:
а) имеет корень, равный 4, , 0;
, 0;
б) не имеет корней;
в) имеет отрицательный корень?
2. Определите, при каких значениях bчисло 3 является корнем уравнения: а) (5+b) x=7+3b;
б) (5b 1) x=15b 3;
в) (4b+1) x=b 5.
3. Для каждого из следующих уравнений, в которых неизвестное число обозначено буквой a, число 1 является корнем уравнения. Найдите, какое число в каждом из уравнений обозначено при этом буквой x?
а) x+1=a; г) (a x)+2=2a;
б) 2x 3=2+a; д) (5 a)+7x=3a;
в) 3(x 1)=x+a. е) ax+3=5.
При выполнении этого задания следует акцентировать внимание учащихся на том, что неизвестное в уравнении обозначено буквой a, а параметр– буквой x.
Если подготовленность учащихся позволяет, то можно рассмотреть и более серьезные задания.
4. Решить уравнения:
а) xa=0
Ответ: при любом ax=a.
б) 5x=a
Ответ: при любом ax=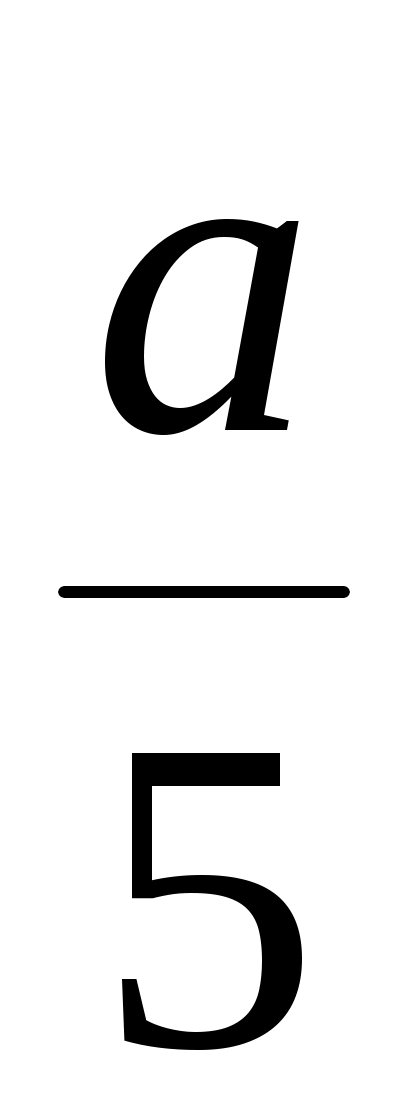 .
.
в) x 2=a
Ответ: при любом ax=2a.
г) x=a
Ответ: при любом ax1=a, x2=a.
Подобные упражнения помогают учащимся привыкнуть к параметру, к необычной форме ответов при решении уравнений. Однако даже такие, казалось бы, совершенно элементарные уравнения часто требуют от учителя подробных комментариев и терпеливых объяснений.
В некоторых сборниках задач фигурируют упражнения такого типа для учащихся 5-6 классов:
Решить уравнение относительно x: a(xa)+b(xb)=x.
Такая формулировка представляется вредной, т.к. младшие школьники не могут решить уравнение с двумя параметрами, проведя его полное исследование.
В таких заданиях следует требовать: выразить x через a и b.
Таким образом, если в течение 5 и 6 классов регулярно в урочной и внеклассной деятельности использовать различные задания пропедевтического содержания к теме "Задачи с параметрами", то это существенно облегчит учащимся изучение этого вопроса на более серьезном и глубоком уровне, поможет сломать стереотипы мышления, разнообразит уроки различных тем. Такие задачи встречают живой отклик у младших школьников, они интересны сами по себе и содержательны.
В 5-6 классах не стоит включать задачи с данным содержанием ни в самостоятельные, ни в контрольные работы, т.к. такие задания сложны для индивидуального решения. Кроме того, к заданиям такого характера учащиеся неоднократно обращаются в 7-8 классах.
Учащимся 5-6 классов предлагаются творческие домашние задания, где требуется придумать аналогичные примеры и решить их.
Пропедевтическая работа важна и интересна, более того, идея приоритета развивающей функции обучения математике является, по существу, формой гуманитаризации математического образования, его ориентации на формирование подрастающего человека как интеллектуальной личности, а реализация гуманитарного потенциала возможна лишь на базе изучения определенного учебного материала.
Зная, что
а)
б)
в) 12a и 10b;
г) 6a и b.
Очевидно, что данные задания решаются учениками 5 класса интуитивно, так как им не известны свойства неравенств, однако они развивают абстрактное мышление, столь необходимое математику.
Можно попросить проиллюстрировать свое утверждение на конкретных значениях a и b.
Тема "Числовые и буквенные выражения"
1. В каждом ряду зрительного зала m мест, а число рядов на n больше, чем мест в ряду. Сколько мест в зрительном зале?
2. В составе пассажирского поезда 3 мягких вагона и 14 купейных вагонов. В каждом мягком вагоне p мест, а в купейном на q мест больше. Сколько всего мест в таком составе поезда?
3. Запишите число, в котором:
а) 8 десятков и x единиц;
б) xдесятков и 8 единиц;
в) x десятков и y единиц;
г) 5 сотен, x десятков и 4 единицы;
д) x сотен, y десятков, z единиц.
Тема "Решение линейных уравнений"
1. При каких значениях a число 5 является корнем уравнения:
а)
б)
в)
2. Какое из двух чисел, обозначенных буквами, больше?
Сравнивая числа в каждом уравнении, докажите, на сколько или во сколько раз больше или меньше:
а)
б)
в)
г)
д)
;
е) c.
3.Может ли при каком-нибудь значении a быть верным равенство:
Тема "Площади и объемы"
1. Составьте формулы для вычисления площадей фигур:

 а) б)
а) б)2. Составьте формулу для вычисления площади заштрихованной части фигуры:

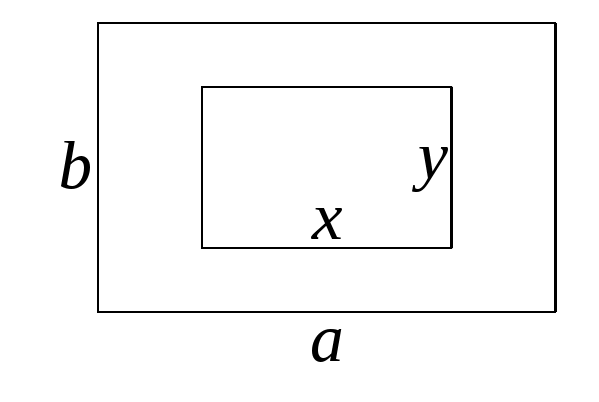 а) б)
а) б) 3. Запишите формулу для вычисления объёма фигуры:

6 класс
Тема "Положительные и отрицательные числа"
1. Зная, что а>b, сравните числа:
а) aи 8 b; б) (a 4) и b.
2. Известно, что а>b>0. Сравните:
а) 15aи 8b; б) 3a и 2b.
3. Положительным или отрицательным числом является значение выражения
4kmn, где mи n-отрицательные числа?
4. Сравнить: а) a и 3a.
Решение: Следует рассмотреть три случая:
Если a<0, то a>3a.
Если a=0, то a=3a, (0=3 0; 0=0).
Если a>0, то a<3a.
б) a и
Решение: 1) Если a<0, то
Если a=0, то
Если a>0, то
При решении задач такого рода желательно иллюстрировать рассуждения на координатной прямой.
Тема "Решение уравнений"
1. При каких значениях k уравнение kz=8:
а) имеет корень, равный 4,
б) не имеет корней;
в) имеет отрицательный корень?
2. Определите, при каких значениях bчисло 3 является корнем уравнения: а) (5+b) x=7+3b;
б) (5b 1) x=15b 3;
в) (4b+1) x=b 5.
3. Для каждого из следующих уравнений, в которых неизвестное число обозначено буквой a, число 1 является корнем уравнения. Найдите, какое число в каждом из уравнений обозначено при этом буквой x?
а) x+1=a; г) (a x)+2=2a;
б) 2x 3=2+a; д) (5 a)+7x=3a;
в) 3(x 1)=x+a. е) ax+3=5.
При выполнении этого задания следует акцентировать внимание учащихся на том, что неизвестное в уравнении обозначено буквой a, а параметр– буквой x.
Если подготовленность учащихся позволяет, то можно рассмотреть и более серьезные задания.
4. Решить уравнения:
а) xa=0
Ответ: при любом ax=a.
б) 5x=a
Ответ: при любом ax=
в) x 2=a
Ответ: при любом ax=2a.
г) x=a
Ответ: при любом ax1=a, x2=a.
Подобные упражнения помогают учащимся привыкнуть к параметру, к необычной форме ответов при решении уравнений. Однако даже такие, казалось бы, совершенно элементарные уравнения часто требуют от учителя подробных комментариев и терпеливых объяснений.
В некоторых сборниках задач фигурируют упражнения такого типа для учащихся 5-6 классов:
Решить уравнение относительно x: a(xa)+b(xb)=x.
Такая формулировка представляется вредной, т.к. младшие школьники не могут решить уравнение с двумя параметрами, проведя его полное исследование.
В таких заданиях следует требовать: выразить x через a и b.
Таким образом, если в течение 5 и 6 классов регулярно в урочной и внеклассной деятельности использовать различные задания пропедевтического содержания к теме "Задачи с параметрами", то это существенно облегчит учащимся изучение этого вопроса на более серьезном и глубоком уровне, поможет сломать стереотипы мышления, разнообразит уроки различных тем. Такие задачи встречают живой отклик у младших школьников, они интересны сами по себе и содержательны.
В 5-6 классах не стоит включать задачи с данным содержанием ни в самостоятельные, ни в контрольные работы, т.к. такие задания сложны для индивидуального решения. Кроме того, к заданиям такого характера учащиеся неоднократно обращаются в 7-8 классах.
Учащимся 5-6 классов предлагаются творческие домашние задания, где требуется придумать аналогичные примеры и решить их.
Пропедевтическая работа важна и интересна, более того, идея приоритета развивающей функции обучения математике является, по существу, формой гуманитаризации математического образования, его ориентации на формирование подрастающего человека как интеллектуальной личности, а реализация гуманитарного потенциала возможна лишь на базе изучения определенного учебного материала.