Файл: Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 58 классов 45.doc
Добавлен: 09.11.2023
Просмотров: 182
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
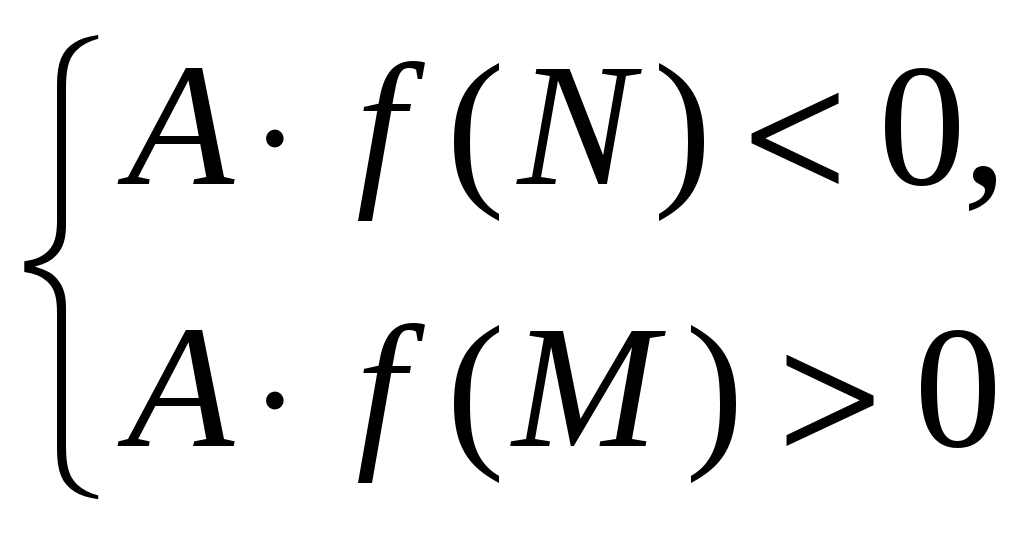
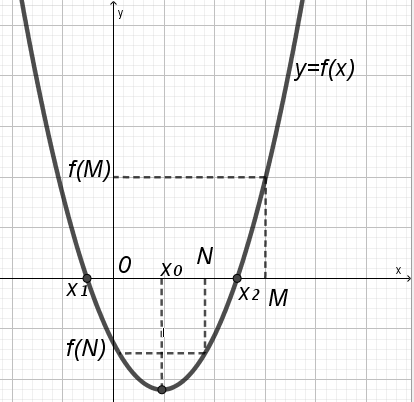
Утверждение 7. Для того, чтобы меньший корень квадратного трехчлена принадлежал интервалу (N; M), а больший не принадлежал, необходимо и достаточно выполнение условий:

У
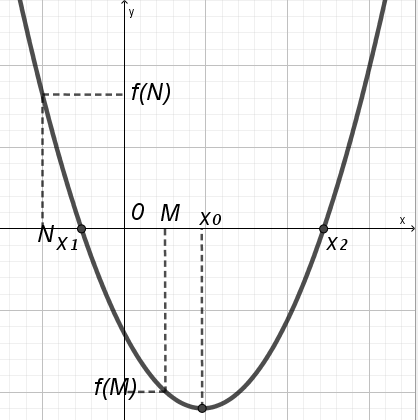 тверждение 8. Для того, чтобы только один корень квадратного трехчлена принадлежал интервалу (N; M), необходимо и достаточно выполнение неравенства
тверждение 8. Для того, чтобы только один корень квадратного трехчлена принадлежал интервалу (N; M), необходимо и достаточно выполнение неравенства f(N)f(M)<0.
При решении задач следует отдельно рассматривать случаи D=0 и A=0.
98. При каких р только один корень уравнения x2рx+6=0 удовлетворяет условию 2<х<5?
Решение: 1) f(2)f(5)<0;
(10 2p) (31 5p)<0 ; 5<p<
2) Если D=0, то уравнение имеет один корень.
D=p224; p224=0; p= 2
а) при p= 2
б) при p=2
Ответ:
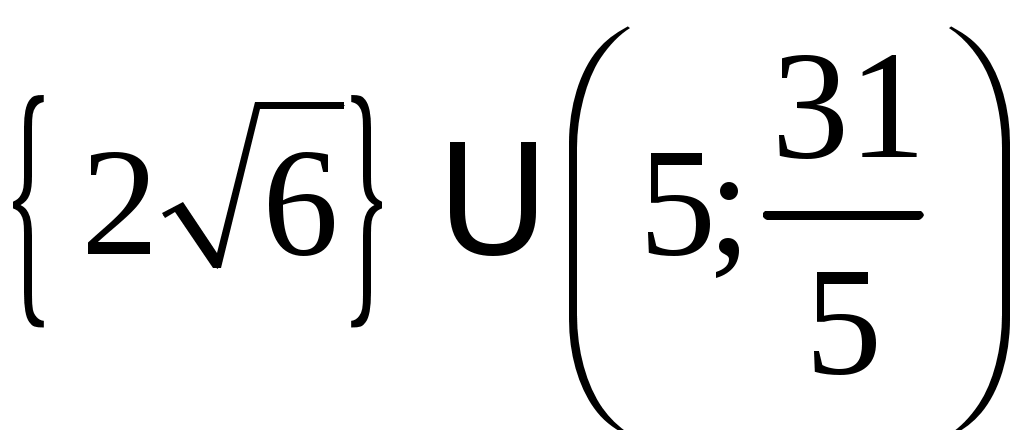 .
.У
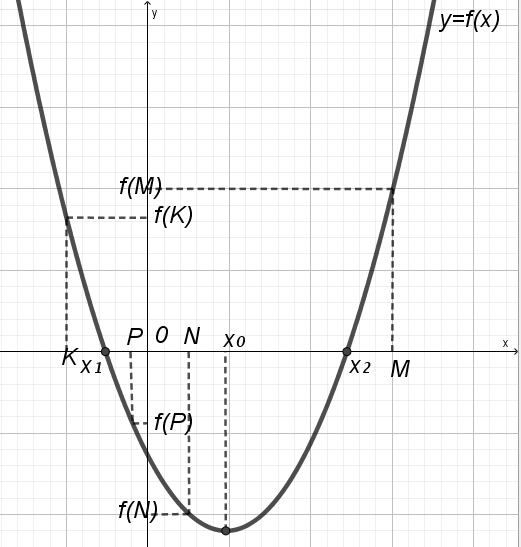 тверждение 9.
тверждение 9.
Для того, чтобы один корень квадратного трехчлена принадлежал интервалу (K; P), а другой интервалу (N; M), необходимо и достаточно выполнение условий:

99. При каких mодин из корней уравнения x2(2m+1)x+m2+m2=0 находится между числами 1 и 3, а второй между числами 4 и 6?
Решение:
1 способ.
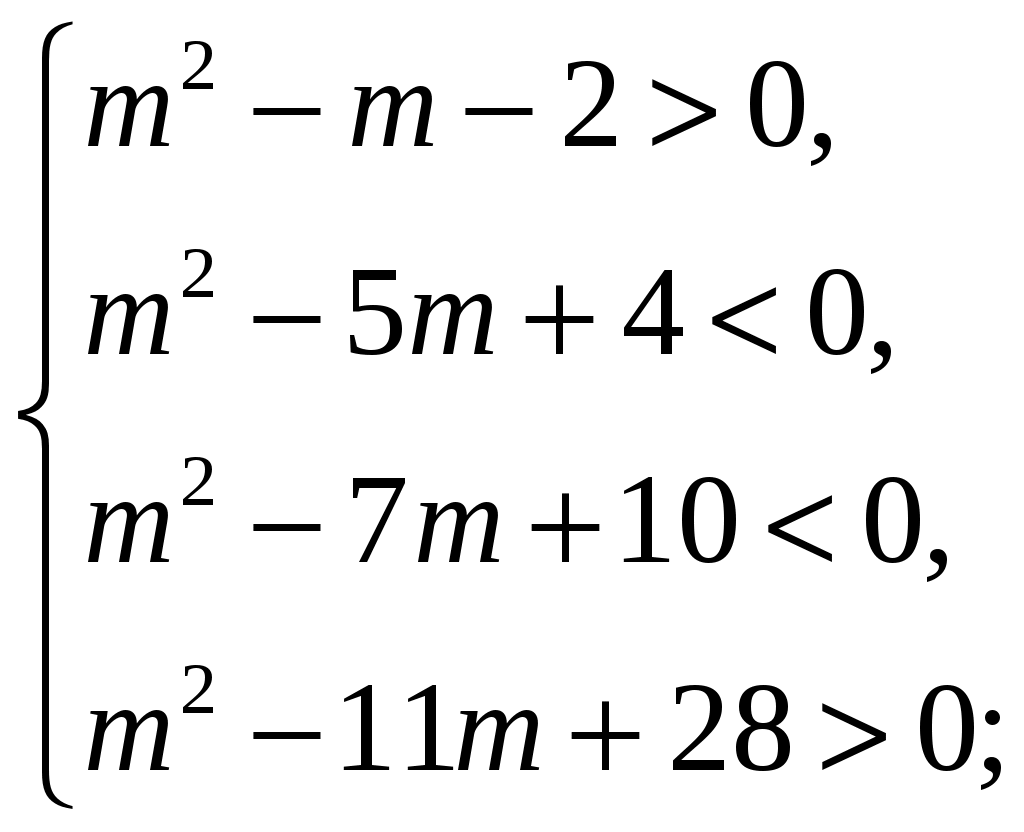

2 способ.
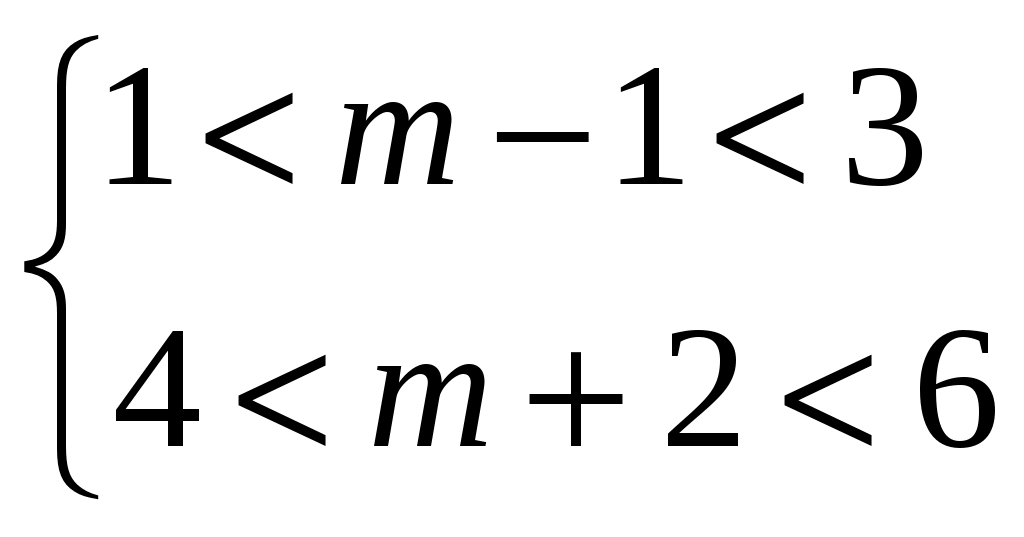
Ответ: (2; 4).
Ключевыми являются утверждения 1-5 и задачи 90, 93, 95, 99. Учителю следует требовать графическую иллюстрацию к задачам и формулировку соответствующего утверждения.
0>2>0>
Уравнения с одной переменной
При изучении уравнений, приводимых к квадратным, можно рассмотреть задачи:
100. При каких значениях а уравнение x2(а+1)x+а=0 имеет 3 различных корня?
Решение:
x2 (а+1)x+а=0; x=t, t 0;
t2(а+1) t+а=0; (1)
Исходное уравнение имеет 3 различных корня, если уравнение (1) имеет t1=0; t2>0
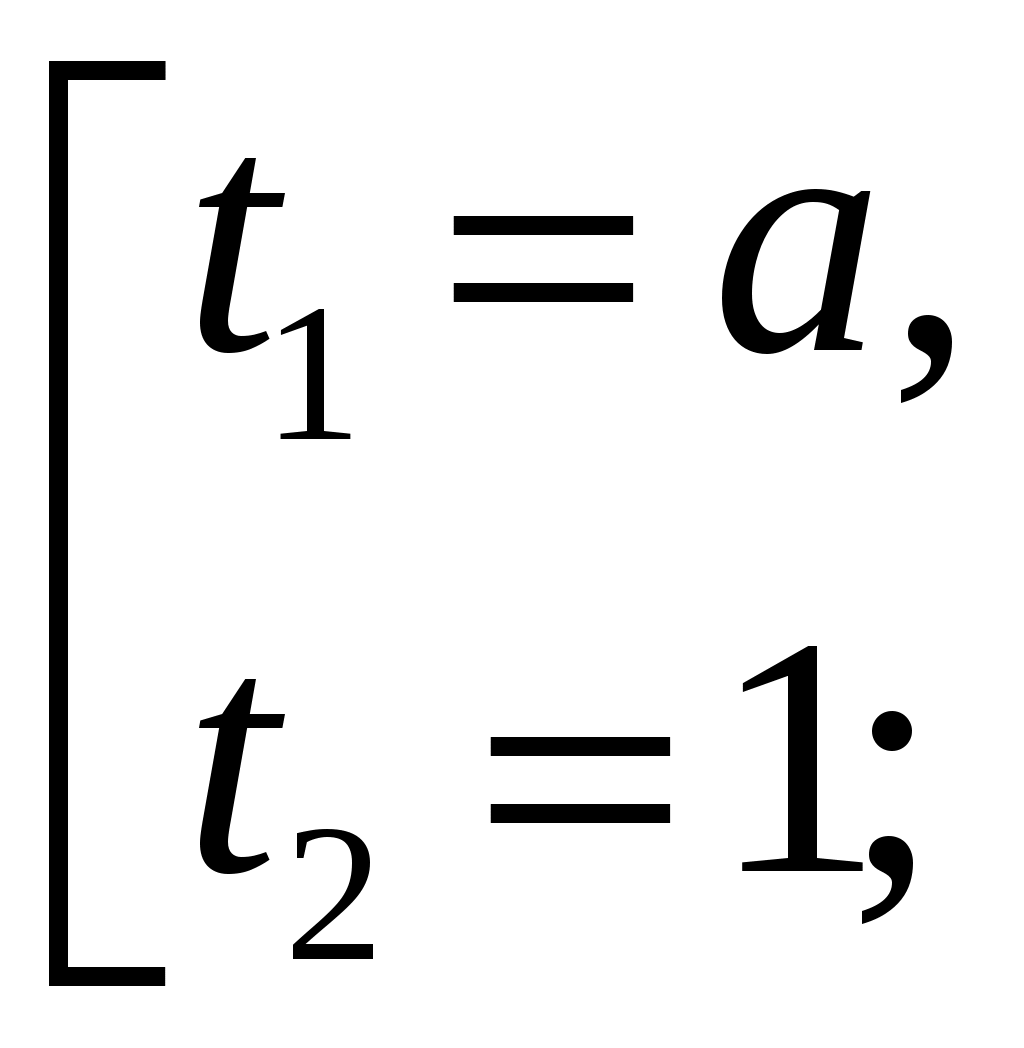


Ответ: а=0.
101. При каких а уравнение x4(3а1)x2+2а2а=0 имеет 2 различных корня?
Решение:
x2=t, t 0;
t2 (3а 1) t+2а2 а=0; (1)
Исходное уравнение имеет 2 различных корня:
1) когда уравнение (1) имеет корни разных знаков, т. е. t1 t2<0,
2аа<0;
0<а<
2) когда уравнение (1) имеет один положительный корень, т. е. D=0, t0>0,
D=9а6а+14(2a a)=a22a+1=(a 1)2;
(a 1)2=0; a=1.
t2 2t+1=0; t0=1.
Ответ: (0; 0,5) U{1}.
Полезно решить ряд задач графическим способом.
102. Определить все значения а, при которых уравнение имеет 2 различных корня:
а) x2=4x+а;
б) 2x=x2+а.
Ответ: а) а= 4, а>0; б) а=1, а<0.
103. При каких а уравнение x+3=ах2 имеет единственное решение?
Ответ: а=0; а=1.
Можно показать учащимся три способа решения этой задачи, сравнить, выбрать более рациональный.
Не следует упускать возможности поразить школьников красотой математики. Использование свойства четности функции превращает сложную, на первый взгляд, задачу в устное упражнение.
104. При каком значении а уравнение x10аx+а2а=0 имеет единственное решение?
Решение: f(x)=x10аx+а2 а четная функция.
Если х0 корень, то и х0 корень, следовательно х0= х0; х0=0 необходимо, но не достаточно.
010а0+а2а=0; а=0; а=1.
Проверка: а) при а=0; x10=0; х=0.
б) при а=1; x10x=0; х=0; х= 1 не удовлетворяет условию.
Ответ: а=0.
105. При каком а уравнение
Ответ: а=1.
Если в 7-9 классах проделать соответствующую работу по изучению параметров, заложить основы материала, то это существенно облегчит решение параметрических задач в 10-11 классах.
Заключение
Прежде всего нужно сказать, что хороших результатов ждать сразу не следует. Если у ученика есть маломальские математические способности, то в итоге он "вырастет" до параметрических задач. Некоторые же дети в силу их психологии, генетического кода так и не смогут общаться с параметрами ни на "ты", ни на "вы". Не следует этого жестко и требовать, раз они не будут связывать свою жизнь с математикой.
Однако же учащиеся, которые "вошли во вкус", способны на большие успехи. Конечно, в основном,
нестандартные методы решения, рациональные приемы они демонстрируют в 10-11 классах, но база для этого должна закладываться кропотливым вдумчивым трудом, начиная с 5 класса.
Целенаправленно изучая этот вопрос, можно достичь запланированных результатов, предполагающих формирование соответствующих умений и навыков.
Вот только как высоко поднять "планку", зависит от обучаемых. Можно ограничиться минимальным уровнем. Это уже хорошо. Можно расширить содержание, добавив тему "Решение систем с параметрами".
Система предложенных заданий саморегулируема. Учитель может по своему усмотрению переставить сами темы в течение года или перенести часть материала на следующий год.
Единственное серьезное требование к учителю-чутко улавливать при объяснении, все ли нюансы изучаемого вопроса "разложились по полочкам" в головах учеников; кропотливо, терпеливо, еще и еще раз объяснять трудные моменты; иметь в запасе много простеньких задач по всем темам. В 7-9 классах главное-качественное изучение блока ключевых задач. С большим разнообразием использования параметра ученики столкнутся в 10-11 классах.
Учитель не должен забывать о цели развития математического мышления: строгости логических построений, четкости речи, полноты рассуждений, точности определений.
Реализация этой цели делает неизбежным отказ от единообразного, уравнительного преподавания математики, унифицирующего как содержание обучения, так и уровень требований к математической подготовке учащихся. А это значит, учитель сам может определять объем дополнительной информации и требования к уровню овладения этой информацией различными учащимися.
Литература
-
Галицкий М.Л., Гольдман А.М., Звавич Л.И., «Сборник задач по алгебре: Учеб. пособие для 8-9 кл. с углубл. изучением математики», 7-е изд. - М.: "Просвещение", 2001. – 271с. -
Гольдич В.А., Злотин С.Е., «3000 задач по алгебре. 5-9 класс», С.-Птб.: "Литера", 2002. – 336с. -
Звавич Л.И., Шляпочник Л.Я., «Контрольные и проверочные работы по алгебре. 7-9 классы», М.: "Дрофа", 2002. – 112с. -
Иванов С.О., Войта Е.А., Коннова Е.Г., Ольховая Л.С., Ханин Д.И., «Математика. Учимся решать задачи с параметром. Подготовка к ЕГЭ-2015: задание 20 (профильный уровень) / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2015. – 64с. -
Козко А.И., Чирский В.Г., «Задачи с параметром и другие сложные задачи». – М.: МЦНМО, 2007. – 296с. -
Коннова Е.Г. «Математика. 9 класс. Подготовка к ГИА. Задания с параметром. – Ростов-на-Дону, Легион, 2014. – 64с. -
Математика. ЕГЭ. Алгебра: задания с развернутым ответом: учебно-методическое пособие / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2016. – 368с. -
Мерзляк А.Г., Якир М.С., «Алгебраический тренажер. Пособие для школьников и абитуриентов», М.: "Илекса", 2007 – 332с. -
Натяганов В.Л., Лужина Л.М., «Методы решения задач с параметрами: Учеб. пособие», М.: Изд-во МГУ, 2003. – 368 с. -
Фридман Л.М., «Учитесь учиться математике», М.: "URSS", 2002. – 120с. -
Шестаков С.А. «ЕГЭ 2016. Математика. Задачи с параметром. Задача 18 (профильный уровень) / Под ред. И.В. Ященко. – М.: МЦНМО, 2016. – 240с. -
Шихова Н.А. Задачи с экономическим содержанием. — М.: ИЛЕКСА, 2018. — 97 с.