Файл: 17.06.вкр.docx

§3. Ограниченность решений однородного уравнения

Выясним условия, при которых решения однородного уравнения 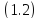ограничены на всей вещественной оси.

Поскольку совокупность решений этого уравнения описывается формулой

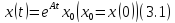
Из условия ограниченности решений следует оценка

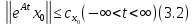
где постоянная 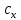зависит только от.

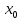Таким образом, совокупность операторов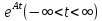ограничена на каждом элементе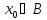. По теореме Банаха - Штейнгауза [2] такая совокупность является равномерно ограниченной

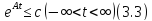
Из 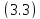следует, что спектр оператора 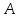лежит на мнимой оси.

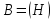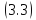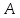Более точный результат можно получить, если фазовое пространство гильбертово. Действительно, условие в силу теоремы I.6.3 [2] выполняется тогда и только тогда, когда оператор подобен эрмитову (косоэрмитову) оператору, умноженному на мнимую единицу:

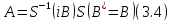
Таким образом, имеет место следующая теорема

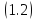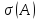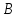Теорема 3.1. Если каждое решение уравнения ограничена на вещественной оси, то спектр лежит на мнимой оси. Если фазовое пространство гильбертово, то ограниченность всех решений имеет место тогда и только тогда, когда оператор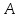 подобен косоэрмитову оператору.

Рассмотрим дифференциальное уравнение второго порядка

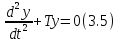
Где .

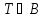Его исследование можно свести к исследованию уравнения первого порядка в сдвоенном фазовом пространстве 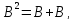элементами которого являются пары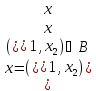с нормой, вычисляемой по формуле

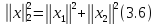
Полагая 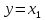,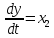мы заменим уравнение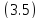системой

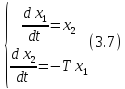
или эквивалентным ей уравнением относительно вектора 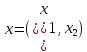в пространстве:

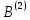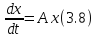
где оператор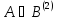определяется операторной матрицей

Нетрудно подсчитать, что

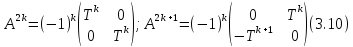
Оператор – функция 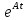, определяющая решения уравнения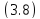, принимает вид

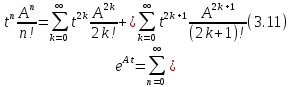
Пользуясь соответствием между скалярными и операторными функциями,

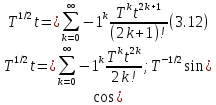
При этих обозначениях из 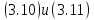следует соотношение

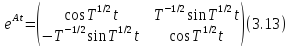
Формула 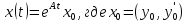, приводит нас теперь к представлению решения уравнения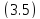, удовлетворяющего условиям

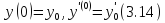
в виде

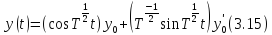
Из формулы 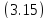следует, что ограниченность при 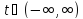каждого решения уравнения 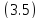эквивалентна ограниченности оператор-функций ,.

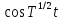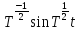Покажем, что достаточно потребовать ограниченность оператор – функции

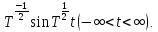
Рассмотрим вектор – функцию

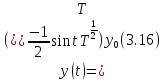
Ее производными являются вектор – функци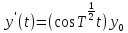и и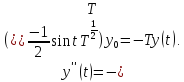По условию при каждом фиксированном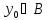вектор – функция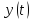, а значит, и

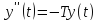, ограничена

Если мы докажем, что ограничена и 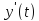, то совокупность операторов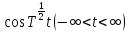 окажется ограниченной на каждом элементе 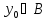, а, следовательно, и ограниченной по норме в силу теоремы Банаха – Штейнгауза [6].

Итак, остается показать, что ограниченности функции 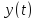и ее второй производной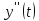следует ограниченность первой производной.

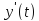Пусть

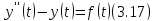
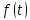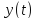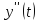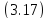Функция ограничена на оси вместе си. Рассматриваякак дифференциальное уравнение, мы можем выразить его ограниченное на всей оси решение при помощи легко проверяемой и известной формулы

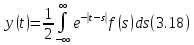
Дифференцируя это выражение по 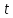, легко показать, что и

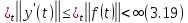
Таким образом, мы получаем, что ограниченность каждого решения уравнения второго порядка 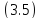на всей оси эквивалентна ограниченности оператор – функции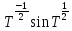.Одновременно доказано следующее утверждение: для того, чтобы все решения уравнения 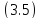были ограничены, необходимо и достаточно, чтобы были ограниченными решения, удовлетворяющие условию.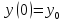

Для случая гильбертовых пространств справедлива следующая теорема и следствие из неё. [6]

Теорема 3.2. Для того чтобы уравнение 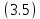в гильбертовом пространстве 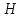было ограниченным на всей оси, необходимо и достаточно, чтобы оператор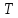был подобен равномерно положительному оператору.

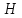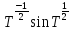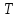Следствие 3.1. В гильбертовом пространстве ограниченность оператор - функцииимеет место тогда и только тогда, когда операторподобен равномерно положительному оператору.

§4.Условия существования ограниченного решения у неоднородного уравнения

Рассмотрим неоднородное уравнение

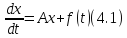
с непрерывной функцией .

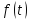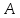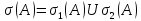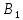Предположим, что спектр оператора распадается на два спектральных множества. Обозначим черези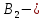инвариантные подпространства оператора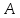, соответствующие этим множествам и, через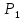и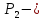соответствующие спектральные проекторы.

Напомним, что [5]

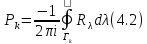
Определение 4.1 Функция вида

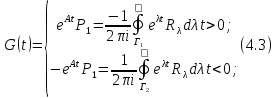
называется оператор – функцией Грина.

Она обладает следующими свойствами [12]:

1. При 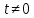оператор – функция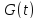непрерывно дифференцируема и удовлетворяет однородному уравнению

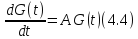
Этот факт непосредственно следует из.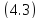

2. Скачок 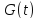в нуле равен единичному оператору.

Действительно,

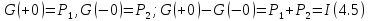
3. Вектор – функция

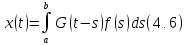
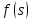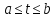где непрерывна, удовлетворяет принеоднородному уравнению.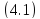

Для доказательства продифференцируем равенство