ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 2210
Скачиваний: 4
155
1.
Стационарная модель равновесия Соловьёва
В этой части изучается модель равновесия Соловьёва на основе уравнения Гр-
эда-Шафранова. В силу осевой симметрии в тороидальной плоскости и, как след-
ствие, инвариантности вдоль угла
θ
, достаточно рассматривать полоидльное сечение
токамака – область
Ω
(рис. 1). Таким образом, можно записать уравнение Грэда-
Шафранова в декартовых координатах
{
R, Z
}
в следующем виде:
−
R
∂
∂R
1
R
∂ψ
∂R
−
∂
2
ψ
∂Z
=
R
2
dp
dψ
+
F
dF
dψ
,
ψ
|
∂
Ω
= 0
,
(1)
где
p
- давледие плазмы,
F
- тороидальный ток,
ψ
- магнитный поток. Имеют место
следующие равенства:
(
p
0
(
ψ
) =
α
=
const,
F
(
ψ
)
F
0
(
ψ
) =
β
=
const
(2)
Описывая полоидальное сечение тора, выразим соотвестсвующие декартовы коор-
динаты:
(
R
=
R
0
+
ax
=
R
0
(1 +
εx
)
,
Z
=
ay,
(3)
где
ε
=
a
R
0
. Теперь уравнение Грэда-Шафранова (1) вместе с (2) может быть выра-
жено в следующем виде:
−
1
a
2
(1 +
εx
)
div
∇
ψ
1 +
εx
=
αR
2
0
(1 +
εx
)
2
+
β
.
(4)
Мы получили уравнение, известное как “уравнение Соловьёва”, выраженное в де-
картовых координатах
{
x, y
}
.
λ
R
0
a
b
R
Z
x
y
Рис. 1.
Координатная система и обозначения:
R
0
- тороидольный радиус,
a, b
- диаметры
по осям
x
и
y
,
λ
- параметр триангуляции
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
156
2.
Нестационарная модель состояния плазмы.
Явление “Current Hole”
2.1.
Постановка модели
Рассматривая цилиндрический случай (
ε
= 0
), имеем следующую модель [6, 8]:
∂ψ
∂t
= [
ψ, φ
] +
η
(
J
−
J
c
)
,
∂ω
∂t
= [
ω, φ
] + [
ψ, J
] +
ν
∆
ω,
J
= ∆
ψ,
ω
= ∆
φ,
(5)
где
[
·
,
·
]
- пуассоновы скобки:
[
a, b
] =
∂a
∂x
∂b
∂y
−
∂a
∂y
∂b
∂x
В системе (5), по сравнению со стационарной моделью, добавлено три новых пара-
метра:
φ
- потенциал скорости,
J
- плотность тороидольного тока,
ω
- завихрённость
плазмы.
2.2.
Численное решение
Для численного интегрирования модели с помощью FreeFem++, дискретизи-
руем модель по оси времени
t
. Далее воспользуемся схемой Кранка-Николсона. В
случае однородного дифференциального уравнения первой степени
∂u
∂t
=
F
(
u
)
, чис-
ленное решение будет иметь вид:
u
n
+1
−
u
n
δt
=
F
(
u
n
) +
F
(
u
n
+1
)
2
.
(6)
Теперь, как и в [7], вспомнив о том, что
F
(
u
n
+1
)
−
F
(
u
n
)
≈
∂F
∂u
(
u
n
)
δu,
выразим
F
(
u
n
+1
)
и подставим в (6). Получим:
1
−
δt
2
∂F
∂u
(
u
n
)
δu
=
δtF
(
u
n
)
.
Запишем теперь схему Кранка-Николсона для системы (5). Обозначим
δψ
=
ψ
n
+1
−
ψ
n
, δφ
=
φ
n
+1
−
φ
n
, δJ
=
J
n
+1
−
J
n
, δω
=
ω
n
+1
−
ω
n
.
(7)
Пусть известны значения неизвестных функций
X
=
{
ψ, φ, J, ω
}
в момент времени
t
n
. Найдём их значения в момент времени
t
n
+1
=
t
n
+
δt
δψ
δt
= [
ψ
n
+
1
2
δψ, φ
n
+
1
2
δφ
] +
η
(
J
n
+
1
2
δJ
−
J
c
)
,
δφ
δt
= [
ω
n
+
1
2
δω, φ
n
+
1
2
δφ
] + [
ψ
n
+
1
2
δψ, J
n
+
1
2
δJ
] +
ν
∆(
ω
n
+
1
2
δω
)
,
δJ
= ∆(
δψ
)
,
δω
= ∆(
δφ
)
,
(8)
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
157
Полагая, что слагаемыми вида
1
4
[
δu, δv
]
, u, v
∈
X
можно пренебречь в силу их мало-
сти, преобразуем систему к следующему виду:
δψ
+
δt
2
[
φ
n
, δψ
]
−
δt
2
[
ψ
n
, δφ
]
−
δt
2
ηδJ
= [
ψ
n
, φ
n
] +
η
(
J
n
−
J
c
)
,
δt
2
[
J
n
, δψ
]
−
δt
2
[
ω
n
, δφ
]
−
δt
2
[
ψ
n
, δJ
] +
δω
+
δt
2
[
φ
n
, δω
]
−
δt
2
ν
∆
ω
=
= [
ω
n
, ψ
n
] + [
ψ
n
, J
n
] +
ν
∆
ω
n
,
∆
δψ
+
δJ
= 0
,
∆
δφ
+
δω
= 0;
(9)
Система (9) в итоге реализуется в пакете FreeFem++.
3.
Вычислительные эксперименты
3.1.
Стационарная модель: уравнение Соловьёва в
D-образной области
В этом разделе будем сравнивать численное решение, полученное в пакете
FreeFem++ с аналитическим решением уравнения Соловьёва (4) [3], которое, по-
лагая, что параметр триангуляции
λ
= 0
, может быть записано в следующем виде:
ψ
(
x, y
) = 1
−
x
−
ε
2
(1
−
x
2
)
2
−
1
−
ε
2
4
(1 +
εx
)
2
a
b
y
2
.
(10)
Следуя [6], параметры
α, β
были выбраны в виде:
α
=
4(
a
2
+
b
2
)
ε
+
a
2
(2
λ
−
ε
3
)
2
R
2
0
εa
2
b
2
,
β
= 0
.
В вычислениях также были использованы параметры:
ε
= 0
.
3
,
R
0
= 5
/
3
,
a
= 0
.
5
,
b
= 0
.
7
, что даёт
α
≈
4
.
35
. D-образная форма сечения задаётся следующим образом:
∂
Ω =
(
(
x, y
)
∈
R
:
x
∈
[
−
1
,
1]
, y
=
±
b
a
s
1
−
(
x
−
ε
2
(1
−
x
2
))
2
(1
−
ε
2
4
)(1 +
εx
)
)
(11)
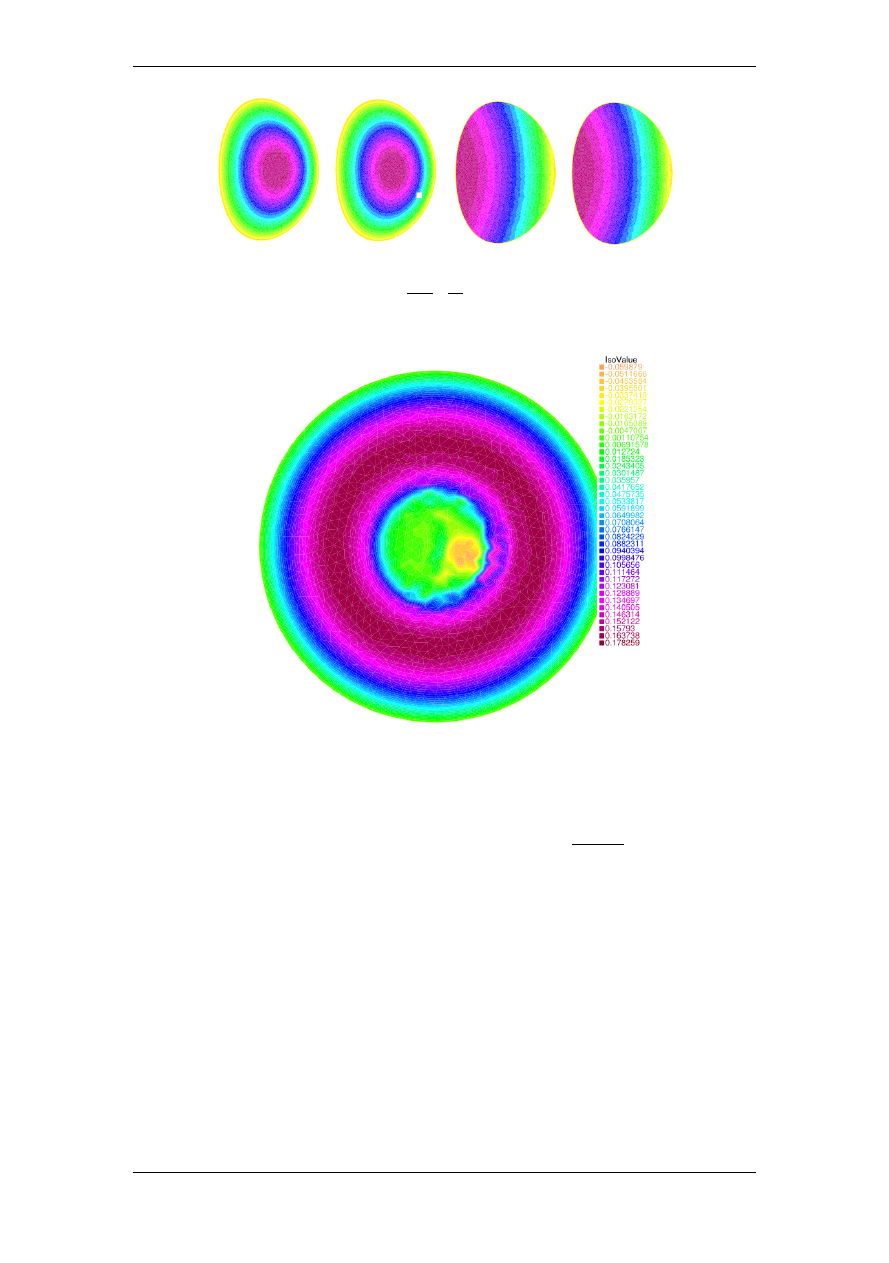
На рисунке 2 представлены результаты вычислений: точное значение магнитного
потока
ψ
ex
, приближённое значение
ψ
, их производные по оси
x
. Ошибка при мощ-
ности сетки
N
Ω
= 255
, определённая как относительная разность
E
(
ψ
) =
||
ψ
−
ψ
ex
||
L
2
||
ψ
ex
||
L
2
≈
0
.
000728738
.
3.2.
Моделирование эффекта “Current Hole” на основе
нестационарной модели
Система (5) моделирует нестационарное поведение функции плотности тока
J
.
Для замыкания системы были добавлены однородные граничные условия; в началь-
ный момент времени функция плотности тока является решением уравнения Гр-
эда-Шафранова (1), ток
J
принимает значения
J
c
, остальные функции принимают
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
158
Рис. 2.
Численное и точное решения уравнения Соловьёва слева направо: точное решение
ψ
ex
, численое решение
ψ
, произнодные
∂ψ
ex
∂x
,
∂ψ
∂x
Рис. 3.
Функция плотности тока в момент времени
t
= 4000
сек
нулевые значения. В поставленной задаче вычисления исходная плотность тока бы-
ла выбрана как [6]:
J
c
= 0
.
2(1
−
r
4
)
−
0
.
2666(1
−
r
2
)
8
,
r
=
p
x
2
+
y
2
.
Вязкость
ν
= 10
−
6
, сопротивление
η
= 10
−
5
. Граница
∂
Ω
является окружностю
радиуса
1
:
∂
Ω =
{
(
x, y
)
, x
= cos
t, y
= sin
t, t
∈
[0
,
2
π
]
}
.
На рис. 3 представлена фунция плотности тока в момент времени
t
= 4000
сек,
полученная на основе схемы Кранка-Николсона в пакете FreeFem++. Вычисления
проводились с шагом
δt
= 1
сек.
Список литературы
1.
К.В.Брушлинский, В.В.Савельев. Магнитные ловушки для удержания плазмы. Мат.
Моделирование, Т. 11, N 5, 1999, с. 3-36.
2.
http://www.femto.com.ua/articles/part_2/4106.html - Токамак - статься из Физической
энциклопедии.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
159
3.
L. S. Soloviev, in: M. A. Leontovich (Ed.). Reviews of Plasma Physics, 6, New York,
Consultant Bureau, 1975, p. 257.
4.
B. Despres, R. Sart. Reduced resistive MHD with general density I: Model and stability
results. 2010.
5.
http://www.freefem.org/ff++/index.htm - FreeFem++ Website.
6.
D. Biskamp. Nonlinear magnetohydrodynamics. Cambridge University Press, 1997.
7.
C. Hirstch. Numerical computations of internal and external flows, Fundamentals of
numerical discretization, vol. 1, John Willey & Sons, 1988.
8.
O. Czarny, G Huysmans. Bezier surfaces and finite elements for mhd simulations. Journal
of computational physics, V. 227, N. 16, 2008, p. 7423-7445.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.