ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 2215
Скачиваний: 4
175
Рассмотренные примеры показывают существенное влияние величины интерва-
ла неопределенности
(
a
2
−
a
1
)
на качество универсального состояния, в частности,
на его близость к целевой функции, при этом значение функционала (12) увеличи-
вается с 0.461699 до 1.05251. Все расчеты проводились в среде Mathematica 8.0.
Список литературы
1.
О
В.О.
Минимизация интервальной квадратичной функции в гильбертовом
пространстве // Сборник материалов XXXVI Дальневосточной Математической
Школы-Семинара имени академика Е.В. Золотова, Владивосток, 4-10 сентября 2012г.
с.175-181.
2.
О В.О.
Интервальная задача оптимального управления в гильбертовом простран-
стве // Журнал вычислительной математики и математической физики 2013, том
53, № 4, с. 26-32;
3.
Ащепков Л.Т., Давыдов Д.В.
Универсальные решения интервальных задач оп-
тимизации и управления. // М.: Наука, 2006.151 с.
4.
Лионс Ж.-Л.
Оптимальное управление системами, описываемыми уравнениями с
частными производными. // Изадательство «Мир», 1972. 416 с.
5.
Алексеев В.М., Тихомиров В.М., Фомин С.В.
Оптимальное управление. // 2-е
изд. — М.: ФИЗМАТЛИТ, 2005. 384 с.
6.
Lions J.-L., Magenes E.
Problemes aux limites non homogenes et applications. // v.1,
2,3. — Paris,1968. 384 с. (Русский перевод первого тома: Неоднородные граничные
задачи и их приложения, изд-во «Мир», М., 1971.)
Понтрягин Л.С.
Обыкновенные
дифференциальные уравнения. // М.: Наука, 1965. 332 с.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
УДК 51-76:57.087
ОЦЕНКА ПРОДУКТИВНОСТИ ЯПОНСКОГО
МОРЯ ПО СПУТНИКОВОЙ ИНФОРМАЦИИ
С.Я. Пак
Институт автоматики и процессов управления ДВО РАН
Россия, 690041, Владивосток, Радио 5
E-mail:
packsa@iacp.dvo.ru
Ключевые слова:
спутниковые данные, динамика хлорофилла, освещен-
ность, температура, критерий Фишера, ассимиляционное число, первичная
продукция
Работа посвящена разработке методов анализа спутниковой информации
с целью построения аналитической зависимости концентрации хлорофил-
ла как основного показателя продуктивности от состояния внешней среды.
Предложена и апробирована базовая модель годовой динамики хлорофил-
ла, параметры которой уточнены с помощью методов регрессионного анали-
за. Выполнен прогнозный расчет, проведено сравнение с данными дистан-
ционных наблюдений. На основании литературных данных о региональных
характеристиках водной среды построены годовые оценки продуктивности
Японского моря.
Введение
Ставится задача оценки объема первичной продукции (ПП) (здесь и далее речь
идет о поверхностном слое воды) по спутниковой информации. Объект исследования
– Японское море, наблюдаемый участок со 127
◦
по 142
◦
восточной долготы и с 34
◦
по
47
◦
северной широты. Методы дистанционного зондирования позволяют получить
данные о концентрации хлорофилла «а», с которой тесно связан объем первичной
продукции. Многие исследователи придерживаются концепции прямо пропорцио-
нальной зависимости одного показателя от другого. Кроме того, дистанционные
измерения дают возможность фиксировать характеристики самой среды, такие как
температура, освещенность, флуоресценция и некоторые др. От них, помимо на-
сыщения биогенными элементами, зависит концентрация хлорофилла в биомассе
фитопланктона (Лупян и др., 2012). Работа поддержана грантом ДВО РАН, проект
09-1-П2-02 по программе фундаментальных исследований Президиума РАН.
1.
Материалы и методы
Интерпретация спутникового сигнала качественно представляет собой равно-
промежуточные пространственные проекции концентраций хлорофилла, фотосин-
тетически активной (ф/а) радиации и температуры в поверхностном слое воды.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
177
Данные за четыре года, с 2008 по 2011 усреднены помесячно. Для анализа число-
вых массивов были использованы методы регрессионного анализа, критерий Фише-
ра, критерий
χ
-квадрат, а также – графическая визуализация, как исходной инфор-
мации, так и данных, полученных в результате моделирования динамики концен-
трации хлорофилла. Для построения прогнозных расчетов использованы числен-
ные методы решения дифференциальных уравнений, включая тригонометрическое
интерполирование и аппроксимацию кусочно-линейными функциями. Параметры,
используемые в модели, получены путем построения регрессионной зависимости по-
казателей хлорофилла от освещенности водной поверхности и температуры воды.
2.
Анализ данных
На первом этапе проанализированы данные за период с 2008 по 2010 гг. Прове-
дено пространственное усреднение помесячных данных о концентрации хлорофил-
ла, об освещенности водной поверхности и температуре воды. Визуальное представ-
ление говорит о зависимости концентраций фитопланктона
(
m
g
/m
3
)
от сезонных
колебаний ф/а радиации
(
Ein
·
m
−
2
day
−
1
)
(
Ein
- Эйнштейн, единица измерения,
означающая моль фотонов) и температуры (
◦
C) в течение всего вегетативного пери-
ода на протяжении трех лет. Поэтому в качестве модельной предложена функция,
выражающая скорость первичного продуцирования, вида:
˜
V
(
t
) = ¯
µ
t
P
(
I
t
)
T
(
θ
t
)
−
E
(
y
t
)
(1)
где
y
t
- концентрация хлорофилла в
(
m
g
/m
3
)
,
¯
µ
t
- максимальная возможная ско-
рость роста массы хлорофилла при некоторой оптимальной температуре
θ
0
, также
зависящая от
t
,
P
(
I
(
t
)
, t
)
– функция зависимости скорости роста
y
t
от показателя
освещенности
I
(
t
)
и от момента времени
t
,
T
(
θ
(
t
)
, t
)
- соответствующая зависимость
от температуры.
E
(
y
t
)
- функция элиминации хлорофилла, которая может происхо-
дить из-за выедания фитопланктона хищниками, в первую очередь, зоопланктоном
и других факторов (Абросов Боголюбов, 1988) . Фактические показатели скорости
роста помесячно определили, как отношение изменения средней массы фитопланто-
на за последующий месяц к усредненному показателю его концентрации в текущем
месяце:
V
f act.
(
t
) =
y
t
+1
−
y
t
y
t
. Тогда значение максимальной скорости роста хлорофил-
ла определятся из условия минимизации функционала:
F
=
N
P
k
=1
(
V
(
k
)
f act.
(
t
)
−
˜
V
(
k
)
(
t
))
2
.
Верхний индекс
(
k
)
соответствует тому, что наблюдаемый показатель усреднен по
k
-ому из
N
географических квадратов, на которые условно разбит наблюдаемый
участок. Для оценки качества регрессионных значений функции
¯
µ
t
провели сравне-
ние динамики изменения усредненной массы наблюдаемого хлорофилла и величины
˜
y
t
, полученной в ходе численного решения дифференциального уравнения:
˙˜
y
t
= ¯
µ
t
P
(
I
t
)
T
(
θ
t
)˜
y
t
−
E
(˜
y
t
)
(2)
Приемлемое согласование
˜
y
t
с наблюдаемой концентрацией хлорофилла
y
t
позво-
лило использовать значения максимальных скоростей первичного продуцирования,
полученных в результате регрессионного анализа наблюдений за период с 2008 по
2010 гг., в качестве основы для составления прогнозного расчета на 2011 год. Гра-
фическое представление (Рис.1) свидетельствует о том, что «модельная» динамика
средней концентрации хлорофилла не противоречит литературным данным о ее се-
зонных изменениях (Моисеев, 1989), (Алексанин и др.,2012).
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
178
Рис. 1.
Сравнительная динамика наблюдаемой и моделируемой концентрации хлорофилла
(
m
g
/m
3
)
в Японском море за четырехлетний период (данные усреднены помесячно и по
пространству).
3.
Статистическая оценка результатов
Считая усредненный по месяцу показатель хлорофилла отдельной вариантой,
рассмотрели четыре временных ряда по количеству наблюдаемых лет. Критерий Фи-
шера, представляющий собой отношение межгрупповой дисперсии к внутригруппо-
вой, позволяет оценить, насколько значима гипотеза о различии в динамике концен-
трации хлорофилла в пределах одного года по сравнению с другим. В результате
получили значение F-критерия, равное 1.313, что значительно меньше предельно-
го критериального значения (F=2.82 при уровне значимости P=0.05 и F=4.26 при
P=0.01). Следовательно, межгодовые различия в динамике хлорофилла, а, значит,
и в сезонных характеристиках – несущественны. Считая 2008-2011 гг. климатически
схожими, на основании критерия
χ
-квадрат оценили, что расхождение величины ,
полученной в результате численного решения уравнения (2), по сравнению с ожида-
емым среднемноголетним помесячным распределением концентрации хлорофилла
также нельзя считать статистически значимым.
4.
Первичная продукция
Объем первичной продукции может быть вычислен в виде произведения концен-
трации хлорофилла на ассимиляционное число. Значение последнего рассматрива-
ется как региональный показатель, зависящий от комплекса благоприятствующих
факторов (Звалинский и др., 2005). Такой подход позволяет построить точечные
оценки объема годовой первичной продукции, основанные на данных спутниковых
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
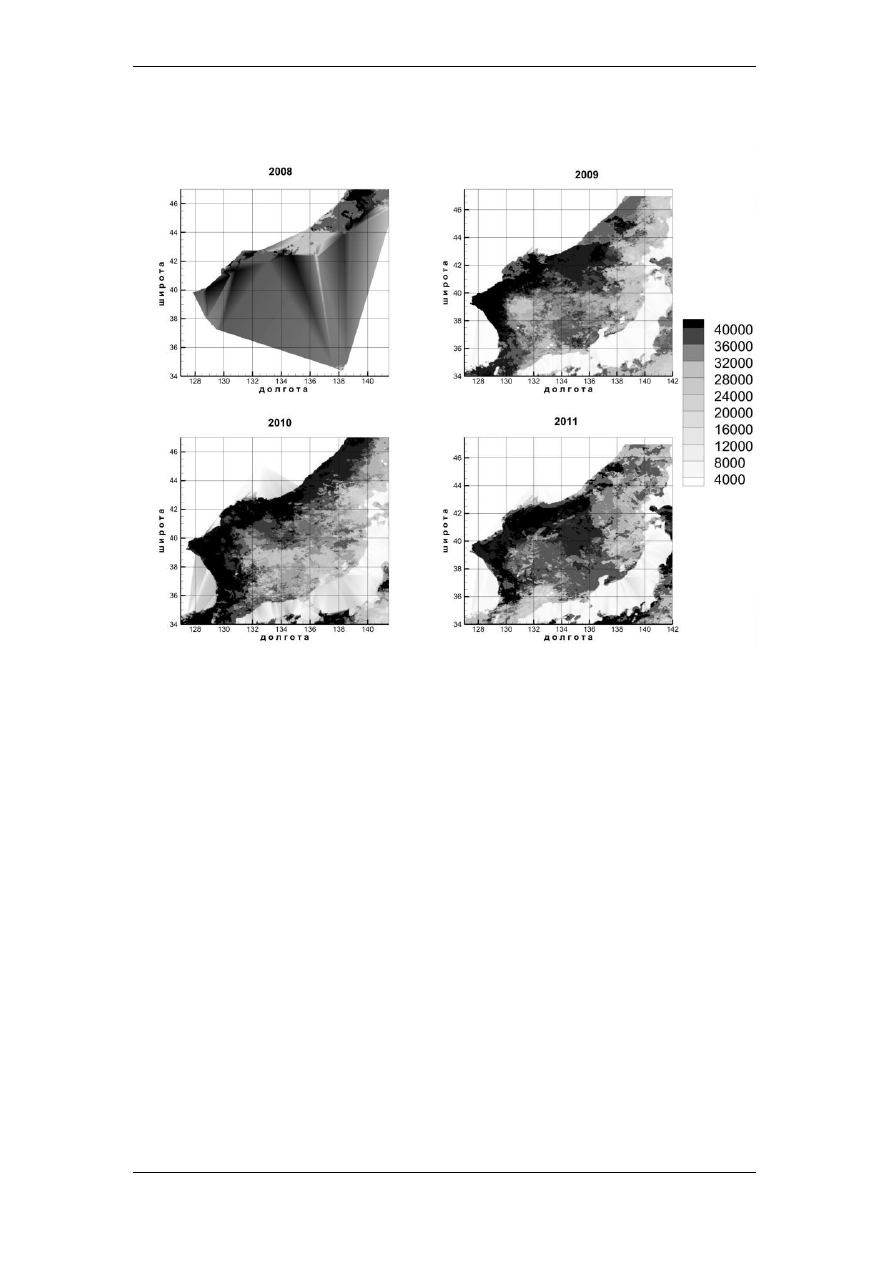
179
наблюдений, усредненных по каждому месяцу текущего года (Рис.2).
Рис. 2.
Сравнительная динамика наблюдаемой и моделируемой концентрации хлорофилла
(
m
g
/m
3
)
в Японском море за четырехлетний период (данные усреднены помесячно и по
пространству).
Поскольку доминирующими в видовом составе Японского моря являются диато-
мовые (Алексанин и др.,2012), и именно они составляют основную долю суммарной
биомассы, благоприятным фактором является температурный диапазон, к которо-
му толерантны данные виды фитопланктона, то есть от 4 до 15 градусов Цельсия
(Насибулина и др., 2012). Кроме того, одной из наиболее значимых предпосылок
интенсивности роста фитопланктона, а стало быть, и увеличения объема первичной
продукции, является достаточное количество минерального питания. Совокупность
этих двух факторов является определяющей при выборе значения ассимиляционно-
го числа.
5.
Выводы и результаты
•
Анализ данных спутниковых наблюдений участка со 127
◦
по 142
◦
восточной
долготы и с 34
◦
по 47
◦
северной широты, покрывающего Японское море, ис-
ключая береговую часть, позволяют сделать следующие выводы:
–
средние концентрации хлорофилла в поверхностном слое воды изменя-
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.