Файл: papers.pdf

УДК 004.42

СИСТЕМА АНАЛИЗА

ТАМОЖЕННЫХ РИСКОВ

М.А. Скаржинец

Дальневосточный Федеральный Университет

Россия, 690091, Владивосток, Суханова 8

E-mail:

powerlord@inbox.ru

Ключевые слова:

риск, таможенные риски, система управления рисками

Введение

Российская таможенная служба играет важную роль в регулировании внешней

торговли страны. Ее основной задачей является обеспечение соблюдения мер тамо-

женно-тарифного регулирования, а также создание условий, способствующих уско-

рению товарооборота через таможенную границу. При постоянно растущем внеш-

неторговом обороте ни одна страна не смогла бы создать таможенную службу, поз-

воляющую проводить тотальный контроль внешнеторговых операций без особого

вреда для внешней торговли. Учитывая это, таможенные службы вынуждены осу-

ществлять таможенный контроль на основе выборочности. С целью оптимизации

этого процесса разрабатываются различные системы управления рисками (СУР).

В России концепция таможенного контроля с применением СУР была утверждена

лишь в 2003 году. СУР, применяемая в Российской таможне, основана на использо-

вании профилей рисков, и, за время применения СУР, таможенная служба накопи-

ла достаточно большую базу статистики нарушений таможенных процедур (НТП).

Информация, хранящаяся в ней, содержит сведения о декларируемом товаре, декла-

ранте, совершённом правонарушении и др. Но на данный момент эта информация

хранится на бумажных носителях в неформализованном виде, что препятствует

её дальнейшей компьютерной обработке. Из этого следует, что в существующей

программной реализации СУР не используются автоматически результаты приме-

нения СУР, т.е. отсутствуют элементы самообучения системы. Для компьютерной

обработке статистики НТП требуется формализовать сам протокол НТП и дать

возможность вносить его в электронную базу данных. Задачей моего исследования

стала разработка программной системы, позволяющей на основе статистики НТП,

и данных, полученных от декларанта, вычислить вероятность нарушения декларан-

том таможенного законодательства.

1.

Анализ предметной области

В процессе исследования были выделены и формализованы основные объек-

ты предметной области «декларирование товаров и транспортных средств»: товар,

Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара

имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.

201

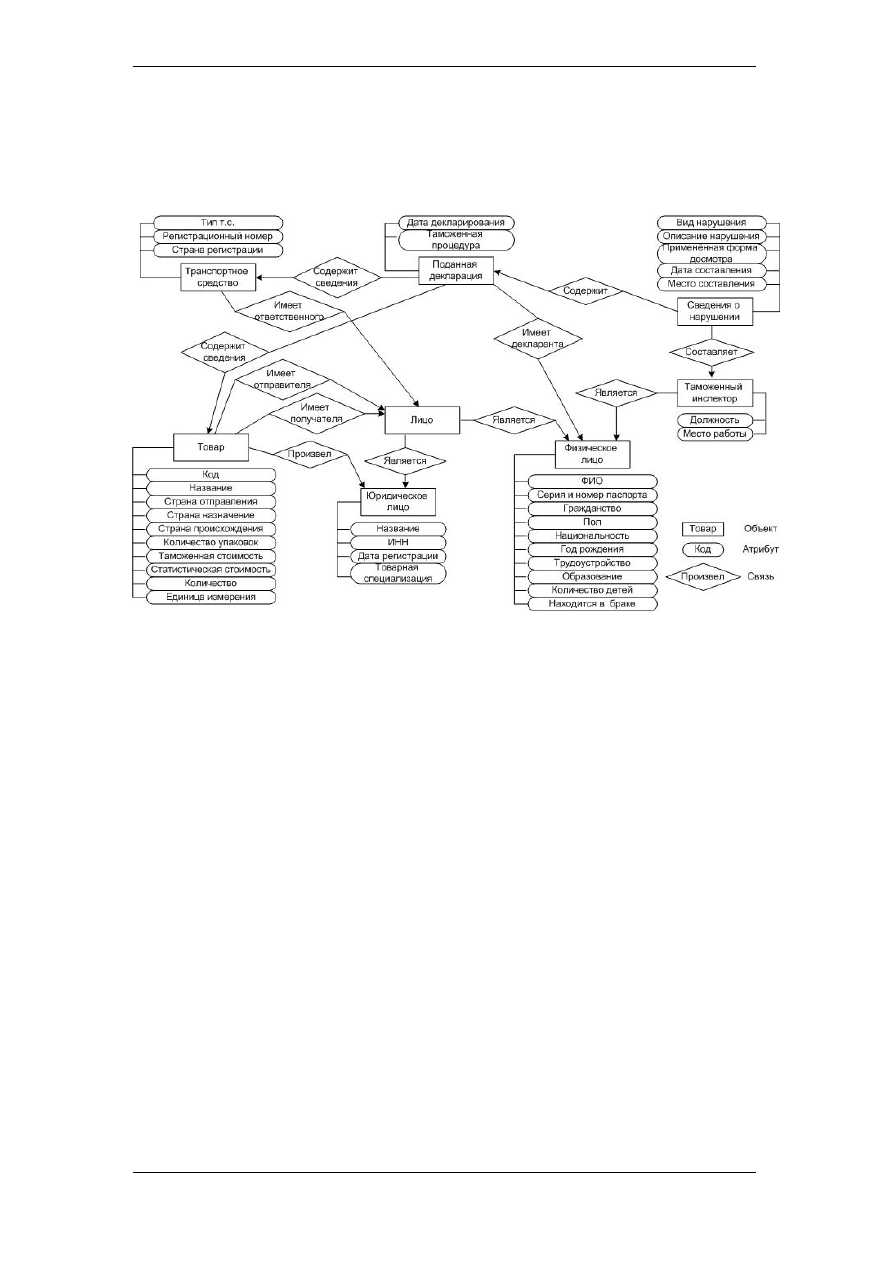
транспортное средство, декларант, декларация (поданная декларация) и протокол

НТП (Сведения о нарушении). В данном контексте под объектом «Декларация» по-

нимается объект, содержащий сведения из всех документов, поданных декларантом.

Формализация проводилась на языке онтологии. ER-модель предметной области

представлена на рис. 1. Для выделенных в процессе анализа объектов были постро-

Рис. 1.

ER-модель ПО

ены связи, позволяющие по данным, поданным декларантом, выявить наиболее ве-

роятные нарушения, вероятность нарушения, и рекомендуемую форму таможенного

досмотра. Наиболее вероятные нарушения состоят из: – Нарушений, характерных

для декларанта и транспортного средства, т.е. из уже совершённых декларантом

(для транспортного средства - совершенных с использованием этого транспортного

средства) нарушений. – Возможных нарушений для товара и транспортного сред-

ства. При этом в БД производится поиск объектов «Поданная декларация», свя-

занных с объектом «Сведения о нарушении», по характеристикам: код товара, тип

транспортного средства. Вероятность нарушения является частотой с точки зрения

статистики и определяется как отношение числа деклараций с выявленным фактом

данного нарушения к общему числу деклараций. Вероятность характерных нару-

шений определяется отношением количества совершённых нарушений к числу де-

клараций, поданных данным декларантом (для транспортного средства - поданных

с указанием этого транспортного средства). Рекомендуемой формой таможенного

досмотра для конкретного нарушения будет являться форма досмотра, при исполь-

зовании которой было выявлено больше всего таких нарушений.

2.

Проектирование и реализация

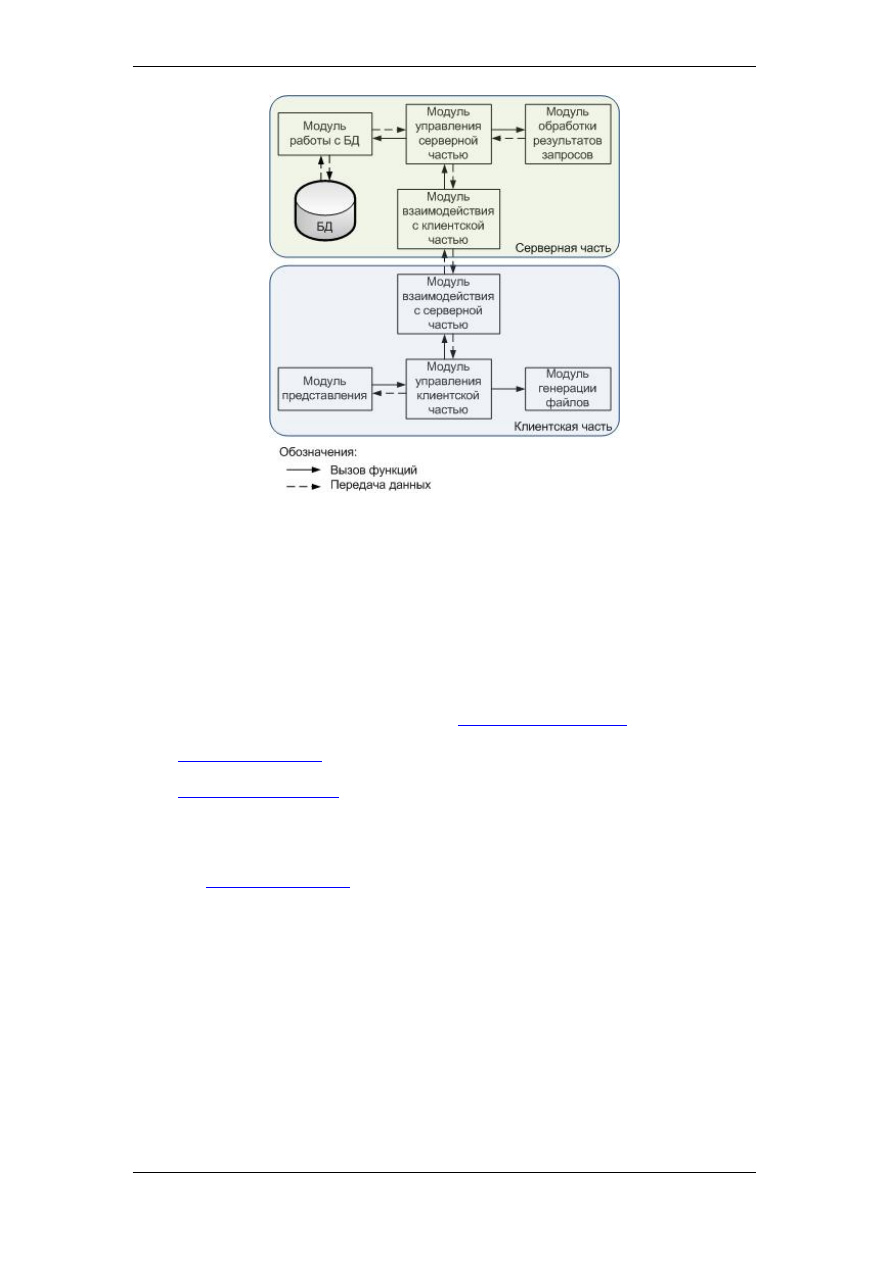
Для реализации системы была выбрана клиент-серверная архитектура. На рис.

2 представлена схема взаимодействия модулей системы:

Прототип системы реа-

Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара

имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.

202

Рис. 2.

Схема взаимодействия модулей

лизован с использованием языка Java. Разработка данной системы проводилась в

рамках выполнения дипломной работы, в дальнейшем планируется провести более

подробный анализ объектов предметной области и связей между ними, усложнить

алгоритм определения вероятности нарушения.

Список литературы

1.

Таможенный кодекс таможенного союза.

http://www.consultant.ru

.

2.

Кодекс Российской Федерации об административных правонарушениях

http://www.garant.ru

.

3.

О применении системы управления рисками в некоторых странах – членах ВТО.

http://rudocs.exdat.com

.

4.

Левченко В.Н. Этапы анализа рисков // Теория и практика общественного развития.
– 2012. – Вып. 7.

5.

Приказ ГТК РФ от 30 марта 2004 г. N 395 "Об утверждении Инструкции о со-
вершении таможенных операций при декларировании товаров в электронной фор-
ме".

http://www.garant.ru

.

Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара

имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.

УДК 517.95

ЧИСЛЕННЫЙ АНАЛИЗ ОБРАТНОЙ

ЭКСТРЕМАЛЬНОЙ ЗАДАЧИ ДЛЯ

УРАВНЕНИЯ ДИФФУЗИИ-РЕАКЦИИ

О.В. Соболева

Институт прикладной математики ДВО РАН

Россия, 690041, Владивосток, Радио 7

E-mail:

soboleva22@mail.ru

Ключевые слова:

уравнение диффузии-реакции, коэффициентные обрат-

ные задачи, массобомен, массоперенос, численный алгоритм

В работе исследована обратная экстремальная задача для стационарного
уравнения диффузии-реакции, рассматриваемого в ограниченной области с
условием Дирихле на границе. Доказана разрешимость указанной задачи,
построена система оптимальности, на основе которой разработан алгоритм
численного решения обратной задачи, основанный на методе Ньютона. Про-
ведены вычислительные эксперименты, показавшие эффективность пред-
ложенного алгорима. Показано влияние параметров входящих в модель, на
точность численного решения посталенной задачи.

1.

Введение

Важную роль в приложениях играют обратные задачи для моделей тепломассо-

переноса. Они заключаются в восстановлении неизвестных плотностей граничных

или распределенных источников либо коэффициентов, входящих в дифференциаль-

ные уравнения или граничные условия модели по дополнительной информации о

решении исходной краевой задачи. Хорошо известно, что изучение обратных задач

можно свести к исследованию соответствующих экстремальных задач при опреде-

ленном выборе минимизируемого функционала качества. На этом пути возникают

обратные экстремальные задачи, для исследования которых можно применять хоро-

шо разработанные методы условной минимизации. Описанию данного подхода для

моделей тепломассопереноса посвящены монографии [1]–[3] и ряд статей, из кото-

рых отметим здесь [4]–[8]. Отметим также работы [9]–[11], в которых аналогичный

подход применяется для решения обратных задач для моделей тепловой конвекции.

Целью настоящей работы является численный анализ решений обратных экстре-

мальных задач для линейной модели массопереноса оприсываемой стационарным

уравнением диффузии-реакции с переменным коэффициентом диффузии, рассмат-

риваемой в ограниченной области при условии Дирихле на границе

Γ

.

Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара

имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.

204

2.

Постановка прямой задачи

Рассмотрим в ограниченной области

Ω

∈

R

d

, d

= 2

,

3

задачу нахождения кон-

центрации

ϕ

(загрязняющего) вещества из соотношений

−

div(

λ

∇

ϕ

) +

kϕ

=

f, ϕ

|

Γ

=

ψ.

(1)

Здесь

λ

≡

λ

(

x

)

>

0

– коэффициент диффузии, зависящий от точки

x

∈

Ω

,

k

≡

k

(

x

)

>

0

– величина, характеризующая распад загрязняющего вещества за счет хи-

мических реакций,

f

(

x

)

– плотность объемных источников,

ψ

(

x

)

– заданная на

Γ

функция. Ниже при анализе краевой и экстремальной задач использовались функ-

циональные пространства Соболева

H

s

(

D

)

и

H

s

(

D

)

,

s

∈

R

. Здесь

D

обозначает либо

область

Ω

, либо границу

Γ

, либо некоторую подобласть

Q

⊂

Ω

. Через

k·k

s

,

|·|

s

будем

обозначать норму и полунорму в

H

s

(Ω)

. Через

k · k

Q

,

k · k

1

,Q

и

(

·

,

·

)

Q

,

(

·

,

·

)

1

,Q

будем

обозначать нормы и скалярные произведения соответственно в пространствах

L

2

(

Q

)

и

H

1

(

Q

)

. Отношение двойственности между пространством

X

и двойственным к

нему

X

∗

будем обозначать через

h·

,

·i

X

∗

×

X

либо просто

h·

,

·i

. Положим

H

s

λ

0

(Ω) =

{

λ

∈

H

s

(Ω) :

λ

>

λ

0

}

, где

λ

0

= const

>

0

,

L

2

+

(Ω) =

{

k

∈

L

2

(Ω) :

k

>

0

в

Ω

}

.

Через

γ

:

H

1

(Ω)

→

H

1

/

2

(Γ)

обозначим оператор следа, через

γ

−

1

r

:

H

1

/

2

(Γ)

→

H

1

(Ω)

– непрерывный правый обратный оператор к

γ

, с которым выполняется соотноше-

ние

γ

◦

γ

−

1

r

ψ

=

ψ

для всех

ψ

∈

H

1

/

2

(Γ)

. Отметим, что в силу теоремы о следах

выполняется неравенство

k

γ

−

1

r

ψ

k

1

6

C

Γ

k

ψ

k

1

/

2

,

Γ

для всех

ψ

∈

H

1

/

2

(Γ)

, где констан-

та

C

Γ

зависит от

Γ

, но не зависит от

ψ

. Подробно о введенных пространствах см.

в [3, гл. 1]. Предположим, что выполняются условия (i)

Γ

∈

C

0

,

1

,

k

∈

L

2

+

(Ω)

; (ii)

f

∈

L

2

(Ω)

; (iii)

λ

∈

H

s

λ

0

(Ω)

,

λ

0

>

0

,

s > d/

2

,

ψ

∈

H

1

/

2

(Γ)

. Введем пространство

T

=

H

1

0

(Ω)

≡ {

η

∈

H

1

(Ω) :

η

= 0

на

Γ

}

. Хорошо известно, что

T

– гильбертово

пространство с нормой

k · k

T

=

k · k

1

, эквивалентной полунорме

| · |

1

в силу нера-

венства Фридрикса–Пуанкар´

е

|

η

|

2

1

>

δ

1

k

η

k

2

1

для всех

η

∈ T

, δ

1

=

const

>

0

. Через

T

∗

≡

H

−

1

(Ω)

обозначим пространство, двойственное к

T

относительно простран-

ства

L

2

(Ω)

. Введем билинейные формы

˜

a

λ

, a

λ

:

H

1

(Ω)

×

H

1

(Ω)

→

R

с помощью

формул

˜

a

λ

(

ϕ, η

) = (

λ

∇

ϕ,

∇

η

) =

Z

Ω

λ

∇

ϕ

· ∇

ηd

x

, a

λ

(

ϕ, η

) = (

λ

∇

ϕ,

∇

η

) + (

kϕ, η

)

.

(2)

Умножим уравнение в (1) на функцию

h

∈ T

и проинтегрируем по

Ω

. Используя

формулу Грина (см. [3, c. 128]) и обозначения (2), приходим к слабой формулировке

задачи (1). Она заключается в нахождении функции

ϕ

∈

H

1

(Ω)

из условий

a

λ

(

ϕ, h

)

≡

(

λ

∇

ϕ,

∇

h

) + (

kϕ, h

) = (

f, h

)

, ϕ

|

Γ

=

ψ.

(3)

Слабым решением задачи (1) назовем функцию

ϕ

∈

H

1

(Ω)

, удовлетворяющую (3).

Из [3] вытекает

Теорема 1.

Пусть при выполнении условия (i)

λ

∈

H

s

λ

0

(Ω)

,

λ

0

>

0

,

s > d/

2

. То-

гда: 1) билинейная форма

a

λ

:

H

1

(Ω)

×

H

1

(Ω)

→

R

непрерывна и коэрцитивна на

T

с константой

λ

∗

=

δ

1

λ

0

; 2) для любой пары функций

(

f, ψ

)

∈

L

2

(Ω)

×

H

1

/

2

(Γ)

задача (3) имеет единственное решение

ϕ

∈

H

1

(Ω)

и справедлива оценка

k

ϕ

k

1

6

C

λ

(

k

f

k

+

k

ψ

k

1

/

2

,

Γ

)

с константой

C

λ

=

λ

−

1

∗

max[1

,

(

λ

∗

+

γ

0

k

λ

k

s

+

γ

1

k

k

k

)

C

Γ

]

; 3) опе-

ратор

(

A

λ

, γ

) :

X

→

Y

,

X

=

H

1

(Ω)

,

Y

= (

T

∗

, H

1

/

2

(Γ))

,

h

A

λ

ϕ, h

i

= (

λ

∇

ϕ,

∇

h

) +

(

kϕ, h

)

∀

ϕ

∈

H

1

(Ω)

, h

∈ T

, осуществляет изоморфизм простраств

X

и

Y

.

Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара

имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.