ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 501
Скачиваний: 1
СОДЕРЖАНИЕ
Требования к уровню освоения содержания дисциплины
Количество информации как мера уменьшения неопределенности знаний
Алфавитный подход к определению количества информации
Характеристики основных типов данных
Кодирование числовой информации в компьютере
Кодирование текстовой информации в компьютере
Кодирование графической информации в компьютере
Кодирование аудио информации в компьютере
ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
Вопросы для самопроверки по теме 2
3. ТЕХНИЧЕСКИЕ СРЕДСТВА РЕАЛИЗАЦИИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Принципы работы электронной вычислительной
ПРОГРАММНЫЕ СРЕДСТВА РЕАЛИЗАЦИИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Файловая структура ОС. Операции с файлами
Инструментальное программное обеспечение ЭВМ
Основные понятия алгоритмических языков. Алфавит.
Прикладное программное обеспечение ЭВМ
Вопросы для самопроверки по теме 4
МОДЕЛИ РЕШЕНИЯ ФУНКЦИОНАЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ ЗАДАЧ
АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ
Вопросы для самопроверки по теме 6
7. ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ
Основные принципы структурного программирования (программирование без GO TO)
Этапы решения задач на компьютере
ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СЕТИ ЭВМ МЕТОДЫ ЗАЩИТЫ ИНФОРМАЦИИ
Электронно-цифровая подпись (ЭЦП)
Классификация антивирусных программ
Вопросы для самопроверки по теме 8
ОТВЕТЫ НА ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Количество информации как мера уменьшения неопределенности знаний
Подход к информации как к мере уменьшения неопределѐнно- сти наших знаний позволяет количественно измерять информацию, полученную через некоторое сообщение.
Например, после сдачи зачета Вы получаете одно из двух ин- формационных сообщений: "зачет" или "незачет", а после сдачи эк- замена одно из четырех информационных сообщений: "2", "3", "4"
или "5".
Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности вашего знания в два раза, так как реализуется один из двух возможных вариантов. Информационное сообщение об оценке за экзамен приводит к уменьшению неопреде- ленности вашего знания в четыре раза, так как получено одно из че- тырех возможных информационных сообщений.
Ясно, что чем более неопределенна первоначальная ситуация, тем больше мы получим новой информации при получении инфор- мационного сообщения о том, как она разрешилась (тем в большее количество раз уменьшится неопределенность знания).
Клод Шеннон предложил в 1948 году формулу для определе- ния количества информации, которую мы получаем после получения одного из N возможных сообщений:
I = – (p1log2p1+ p2log2p2+… pilog2pi+…+ pNlog2pN)
Здесь pi – вероятность того, что будет получено именно i-е со- общение. Если все сообщения равновероятны, то все pi=1/N, и из этой формулы получается формула Хартли:
I = log2N
Для количественного выражения любой величины необходимо сначала определить единицу измерения. Так, для измерения длины
в качестве единицы выбран метр, для измерения массы - килограмм и
т. д. Аналогично, для определения количества информации необхо- димо ввести единицу измерения.
Из формулы Хартли следует: если I=1, то N=2, то есть в каче- стве единицы измерения информации можно взять тот объѐм инфор- мации, который мы получаем при принятии сигнала о том, что же произошло в ситуации с двумя возможными исходами. Такая едини- ца названа битом.
Наряду с единицей бит иногда используют в качестве единиц информации количества, взятые по логарифмам с другими основа- ниями: дит – по десятичному логарифму (за единицу информации выбирается количество информации, необходимой для различения десяти равновероятных сообщений), нат – по натуральному основа- нию.
Используя формулу Хартли можно, также, зная количество информации, пришедшее с одним из равновероятных сообщений, оп- ределить, сколько сообщений вообще можно было ожидать в данной ситуации. Решив это уравнение относительно N, получим при равно- вероятных исходах:
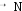 I = log2N = 2I
I = log2N = 2IНапример, на экзамене вы берете экзаменационный билет, и учитель сообщает, что зрительное информационное сообщение о его номере несет 5 бит информации. Если вы хотите определить ко- личество экзаменационных билетов, то достаточно определить коли- чество возможных информационных сообщений об их номерах из формулы Хартли:
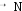 5 = log2N = 25 = 32.
5 = log2N = 25 = 32.Таким образом, количество экзаменационных билетов равно
32.
Задача: Представьте себе, что вы управляете движением ро-
бота и можете задавать направление его движения с помощью ин- формационных сообщений: "север", "северо-восток", "восток", "юго- восток", "юг", "юго-запад", "запад" и "северо-запад" (рис. 1.1). Какое
количество информации будет получать робот после каждого сооб- щения?
-
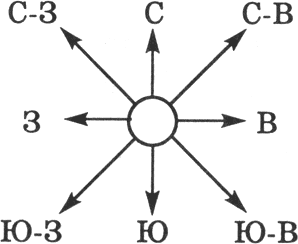
Рис. 1.1. Управление роботом с использова- нием информационных сообщений
В этой задаче робот может получить 8 разных информацион- ных сообщений. Формула Хартли принимает вид уравнения относи- тельно I:
8 = 2I
Так как 8 = 23, получаем
Количество информации, которое несет роботу каждое инфор- мационное сообщение, равно 3 битам.
- 1 2 3 4 5 6 7 8 9 ... 45
Алфавитный подход к определению количества информации
При алфавитном подходе к определению количества информа- ции отвлекаются от содержания информации и рассматривают ин- формационное сообщение как последовательность знаков определен- ной знаковой системы.
Представим себе, что необходимо передать информационное сообщение по каналу передачи информации от отправителя к получа- телю. Пусть сообщение кодируется с помощью знаковой системы, алфавит которой состоит из N знаков {1, ..., N} и вероятности появ- ления каждого знака в сообщении равны.
В простейшем случае, когда длина кода сообщения составляет один знак, отправитель может послать N разных сообщений. Количе- ство информации I, которое несет каждое сообщение, то есть один знак, можно рассчитать по формуле Хартли.
I = log2N
Эта величина называется информационнойемкостьюзнака. С помощью этой формулы можно, например, определить информа- ционную емкость знака двоичной знаковой системы:
I = log22 = 1 бит
Интересно, что сама единица измерения количества информа- ции "бит" (bit) получила свое название от английского словосочета- ния "binary digit" – "двоичная цифра".
Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. В качестве примера определим количество информации, которое несет буква русского алфавита. В русский алфавит входят 33 буквы, однако на практике часто для передачи сообщений используются только 32 буквы (исключается буква "ѐ").
С помощью формулы Хартли определим количество информа- ции, которое несет буква русского алфавита:
N = 32 I = log232 I = log225 I=5 бит.
Таким образом, информационная емкость буквы русского ал- фавита равна 5 битам (если считать, что все буквы используются в сообщении с равной вероятностью).
Количество информации, которое несет знак, зависит от веро- ятности его получения. Если получатель заранее точно знает, какой знак придет, то полученное количество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его ин- формационная емкость.
Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации. Если знаки не- сут одинаковое количество информации, то количество информации Ic в сообщении можно подсчитать, умножив количество информации Iз, которое несет один знак, на длину кода К (количество знаков в со- общении):
Ic = Iз * K
Например, каждая цифра двоичного компьютерного кода несет информацию в 1 бит. Следовательно, две цифры несут информацию в 2 бита, три цифры - в 3 бита и т. д. Количество информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.1).
Таблица 1.1.
Количество информации, которое несет двоичный компьютерный код
-
Двоичный компьютерный код
111
01
11
011
0001
Количество информации
3 бит
2 бит
2 бит
3 бит
4 бит
В русской письменной речи частота использования букв в тек- сте различна, так в среднем на 1000 знаков осмысленного текста при- ходится 200 букв "а" и в сто раз меньшее количество буквы "ф" (все-