ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 481
Скачиваний: 1
СОДЕРЖАНИЕ
Требования к уровню освоения содержания дисциплины
Количество информации как мера уменьшения неопределенности знаний
Алфавитный подход к определению количества информации
Характеристики основных типов данных
Кодирование числовой информации в компьютере
Кодирование текстовой информации в компьютере
Кодирование графической информации в компьютере
Кодирование аудио информации в компьютере
ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
Вопросы для самопроверки по теме 2
3. ТЕХНИЧЕСКИЕ СРЕДСТВА РЕАЛИЗАЦИИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Принципы работы электронной вычислительной
ПРОГРАММНЫЕ СРЕДСТВА РЕАЛИЗАЦИИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Файловая структура ОС. Операции с файлами
Инструментальное программное обеспечение ЭВМ
Основные понятия алгоритмических языков. Алфавит.
Прикладное программное обеспечение ЭВМ
Вопросы для самопроверки по теме 4
МОДЕЛИ РЕШЕНИЯ ФУНКЦИОНАЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ ЗАДАЧ
АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ
Вопросы для самопроверки по теме 6
7. ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ
Основные принципы структурного программирования (программирование без GO TO)
Этапы решения задач на компьютере
ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СЕТИ ЭВМ МЕТОДЫ ЗАЩИТЫ ИНФОРМАЦИИ
Электронно-цифровая подпись (ЭЦП)
Классификация антивирусных программ
Вопросы для самопроверки по теме 8
ОТВЕТЫ НА ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
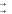
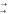 100011111110102 10 001 111 111 0102 217728
100011111110102 10 001 111 111 0102 217728100011111110102 10 0011 1111 10102 23FA16
Таблица 1.3.
Таблица соответствия между начальными двоичными, восьмеричными, шестнадцатеричными и десятичными числами:
-
Основание системы
счисления
Вид числа
10
0
1
2
3
4
5
6
7
2
0000
0001
0010
0011
0100
0101
0110
0111
8
00
01
02
03
04
05
06
07
16
0
1
2
3
4
5
6
7
10
8
9
10
11
12
13
14
15
2
1000
1001
1010
1011
1100
1101
1110
1111
8
10
11
12
13
14
15
16
17
16
8
9
A
B
C
D
E
F
- 1 2 3 4 5 6 7 8 9 10 ... 45
Характеристики основных типов данных
Наряду с информационным смыслом термином бит в вычис- лительной технике используют для обозначения наименьшего эле-
мента памяти, необходимого для хранения одного из двух знаков: «0» или «1», используемых для представления данных и команд внутри компьютера.
Бит очень удобен для использования двоичной формы пред- ставления информации. Для каждого типа информации (символьный, текстовый, графический, числовой) был найден способ представить ее в едином виде как последовательность, использующую в разных комбинациях только два символа. Каждая такая последовательность называется двоичным кодом. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим числом простых однотипных элементов, чем с небольшим числом сложных.
Двоичные символы могут представляться любыми способами: буквами А, Б; словами ДА, НЕТ, двумя разными, но устойчивыми со- стояниями системы и т. д. Для простоты записи были выбраны циф- ры 0 и 1.
Характеристики основных типов данных, которые обрабаты- ваются современными компьютерами, приведены в табл.1.4.
Таблица 1.4.
Основные виды данных, с которыми работает ЭВМ.
| Тип данных | Название типа данных | Объем памяти | Диапазон значе- ний |
| Целые числа (формат с фик- сированной за- пятой) | Byte (короткое целое) | 1 байт | От – 127 до + 127 |
| Integer | 2 байта | От – 32768 до + 32767 | |
| Long | 4 байта | От – 2 147 483 648 до + 2 147 483 647 | |
| Вещественные числа (формат с плавающей запятой) | Single (7 – 8 значащих цифр) | 4 байта | От – 1,4*10-45 до + 3,4*1038 |
| Double (15 – 16 значащих цифр) | 8 байт | от – 5,0*10-324 до + 1,7*10308 | |
| Символьные | Первоначальные таблицы 8- битовых кодировок (ASCII, КОИ8-Р, CP1251, CP866, ISO 8859-5 и другие) | 1 байт | 256 символов |
| Юникод | 2 байта | 65536 символов | |
| Логические (Boolean) | 1 байт | 0; 1 | |
- 1 ... 4 5 6 7 8 9 10 11 ... 45
Кодирование числовой информации в компьютере
Числа в компьютере переводятся в двоичную позиционную систему и размещаются в отведенном для них месте в формате с фик- сированной или плавающей запятой.
В формате с фиксированной запятой каждому разряду па- мяти всегда соответствует один и тот же разряд числа. Например, при кодировании целых чисел, младший разряд числа размещается в по- следнем (крайнем справа) бите памяти, отведенной под код числа. То есть место для дробной части числа не предусматривается.
Для кодирования целых чисел используется три варианта ко- дировок: прямой, обратный и дополнительный коды. Для положи- тельных целых чисел используется прямой код. Обратный и допол- нительный коды добавляются при кодировании отрицательных чи- сел. Они позволяют заменить операцию вычитания на сложение, что существенно упрощает работу процессора и увеличивает его быстро- действие.
В прямом коде первый бит памяти, отведѐнный под число, по- казывает знак числа: 0 – положительное, 1 – отрицательное. Осталь- ные биты отводятся под двоичный код модуля числа. Примеры:
12710 → 011111112 ;
– 12710 → 111111112;
110 → 000000012;
– 110 → 100000012.
В обратном коде все двоичные цифры, кроме первой (указы- вающей на знак), инвертируют: заменяют 0 → 1, 1→ 0. Примеры:
– 12710 → 111111112 → 100000002;
– 110 → 111111102 → 000000012.
Дополнительный код получают из обратного кода целого от- рицательного числа, прибавляя к нему 12. Примеры:
– 110 → 111111102 → 100000012 →1111 11102;
– 12710 → 11111111
2 → 100000002 → 1000 00012
В формате с плавающей запятой представляются вещест- венные числа (предполагается, что они могут содержать дробную часть). В этом формате число заносится в память компьютера в экс- поненциальной форме, то есть в виде двух сомножителей: мантиссы(дроби, в которой первая значащая цифра стоит сразу после запятой)
и основания системы счисления в соответствующей степени (поряд-ке). Примеры для десятичной системы счисления приведены в табли- це 1.5.
Таблица 1.5 Примеры перевода вещественных чисел в экспоненциальную форму
-
Вещественное число
Экспоненциальная
форма
Мантисса
Порядок
98567
0,98567*105
0,98567
5
– 98567
– 0,98567*105
–0,98567
5
98,567
0,98567*102
0,98567
2
– 0,0009856
– 0,9856*10-3
– 0,9856
–3
В байтах, отведенных для записи числа, выделяются опреде- ленные разряды для хранения всех фрагментов числа: знаков мантис- сы и порядка, их абсолютных значений. Пример (код максимального положительного числа):
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Знак и значение порядка | Знак и значение мантиссы | ||||||||||||||||||||||