Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 382

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Деформация, остающаяся в теле после разгрузки, получила названиеостаточной или пластичной, а способность тела приобретать пластическую деформацию – пластичность.

Сплошность

7.1.1. Общие замечания

Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу

Методика расчёта

Нагрузка, при которой прямолинейная форма перестаёт быть формой устойчивого равновесия, называется критической(Fкр ). Таким образом, исследование устойчивости стержня заключается в определении Fкр. Для обеспечения устойчивости допускаются нагрузки, составляющие лишь часть критических. Отношение критической нагрузки Fкр к её допускаемой величине ([F]y) называется коэффициентом устойчивости: (11.1)Коэффициент ny зависит от материала стержня. Его рекомендуемые величины находятся в пределах: для стальных стоек 1.5…3; для деревянных 2.5…3.5; для чугунных 4.5…5.5. Метод Эйлера для определения критической силы. Формула Эйлера.Для исследования устойчивости равновесия упругих систем имеется несколько методов: метод малых колебаний, энергетический метод и др. В инженерной практике для невесомых стержней с нагрузкой, приложенной точно в центре тяжести торцовых сечений и параллельно продольной оси стержня используют более простой метод – метод Эйлера.Метод Эйлера основан на анализе разветвления форм равновесия упругой системы. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма. Для вывода формулы Эйлера рассмотрим шарнирно - опёртый, центрально - сжатый стержень постоянного сечения (рис. 11. 3) в слегка отклонённом состоянии от прямолинейной формы.Изгибающий момент в произвольном сечении равенF (11.2)Дифференциальное уравнение изгиба стержня запишется в виде: (11.3)или (11.4)где (11.5)Интеграл дифференциального уравнения (11.4) имеет вид (11.6)Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z=0 и Следовательно, уравнение оси изогнутого бруса (6) примет вид (11.7)Таким образом, стержень изгибается по синусоиде.Второе граничное условие: при z=l и  Bsinkl=0Это условие выполняется в двух случаях:1) В=0; 2) sinkl=0Первый случай нас не интересует, так как при В=0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.Второе условие sinkl=0 дает kl= 2 3 nучтя значение k (11.5), получим: Итак, получено не одно, а множество значений критической силы. Каждой критической силе соответствует своя форма равновесия (рис. 11.4). Подставляя найденное значение k в уравнение оси изогнутого бруса (11.7), замечаем, что при первой критической силе стержень изгибается по одной полуволне синусоиды, а при всех последующих число полуволн равно номеру соответствующей критической силы. Равновесие, соответствующее первой форме изгиба, является устойчивым, а все всем остальным – неустойчивым.Для инженерных расчетов практический интерес представляет только наименьшая критическая сила (11.8)Эту формулу в 1744 г. впервые получил Леонард Эйлер, поэтому она называется формулой Эйлера, а определяемую этой формулой критическую силу – эйлеровой силой.Из формулы (11.8) видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.Таким образом, выясняется резкая разница между работой стержня на растяжение и на сжатие. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и поэтому различна для разных сортов стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина. Предельная растягивающая сила не зависит от длины стержня, в то время как при сжатии она быстро падает с увеличением длины.Продольный изгиб сжатых стержней особенно опасен потому, что он наступает внезапно, и поэтому его трудно предупредить. В растянутых стержнях признаки опасного состояния часто наступают задолго до разрушения, а в сжатых стержнях каких- либо заметных признаков потери устойчивости, как правило, установить не удается.11.3. Влияние способов закрепления концов стержня на величинукритической силыНа рис. 11.5 показаны различные случаи закрепления концов сжатого стержня. Для каждого случая необходимо проводить свое решение аналогичное тому, что сделано в предыдущем параграфе для шарнирно опертого стержня. Эти решения показывают, что для всех случаев, изображенных на рис. 11.5, критическую силу можно представить в виде формулы: (11.9)где   коэффициент приведения длины, а величина ll0называется приведенной (свободной) длиной. Понятие о приведенной длине было впервые введено профессором Петербургского института путей сообщения Ф.С. Ясинским (1892).Свободная длина l0может быть истолкована как некоторая условная длина шарнирно опертого стержня, имеющего такую же критическую силу, как заданный стержень. В отдельных случаях это положение вытекает из чисто геометрического толкования (длина полуволны синусоды). Так, например, если стержень заделан одним концом, рассматривать как половину стержня, шарнирно опертого по концам, то l0= 2l. Следовательно, =2.Для стержня, заделанного двумя концами, длина полуволны, замеренная между двумя точками перегиба, где Мх=0,составит половину длины стержня, следовательно, для этого случая =0,5. 11.4. Пределы применимости формулы Эйлера. Формула Ясинского Формула Эйлера, полученная более 267 лет назад, долгое время являлась предметом дискуссий. Формула Эйлера для некоторых случаев не подтверждалась экспериментами. Объясняется это тем, что формула Эйлера выводилась в предположении, что при любом значении силы стержень работает в пределах упругих деформаций с использованием закона Гука. По этому формулу Эйлера нельзя применять в случаях, когда критические напряжения больше предела пропорциональности. Для установления предела применимости формулы Эйлера найдем Здесь радиус инерции. Обозначим через  Величина  называется гибкостью стержня.Итак, (11.10) Это так же формула Эйлера, но записанная для критического напряжения, а не для критической силы. Принято изображать уравнение (11.10) в координатах кр -(рис. 11.6). Полученную кривую часто называют гиперболой Эйлера. Как видно из уравнения (11.10), при малых гибкостях критические напряжения могут значительно превосходить предел прочности материала. Действительно короткие и толстые стержни (например, кубы, имеющие гибкость 

Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.

Так как

Отсюда определяется меридиональное напряжение т.

Напряженное состояние является двухосным

Из формулы Лапласа находим

где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки

15. Динамическое действие нагрузок

15. Динамическое действие нагрузок…………………………………..216



Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут во много раз превосходят те же нагрузки, приложенные статически.

Законы изменения нагрузок во времени могут иметь весьма сложный характер.
1.5. Внутренние силы в стержне и их определение
В процессе деформации стержня, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы. По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих сил применяют метод сечений (РОЗУ см. ТМ); надо мысленно рассечь стержень (cм. рис. 1.1.), находящийся в равновесии, на две части и рассмотреть равновесие одной из них, например, части D.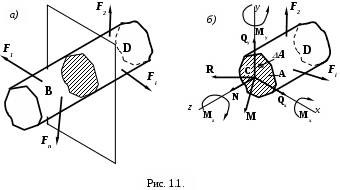



Выберем оси координат x,y,z c началом в центре тяжести сечения (точка С) так, чтобы оси Сх и Су лежали в его плоскости.

Со стороны отброшенной части на часть D действует система внутренних сил, распределённых по всему сечению. Эту систему сведём к главному вектору R и главному моменту М.

Представим: R в виде трех составляющих: N, Qx, Qy;

M в виде трех составляющих: Mx, My, Mz.

ВеличиныN, Qx, Qy, Mx, My, Mz- принято называть внутренними силовыми факторами.

Каждая из этих величин имеет своё название:

N – нормальная (продольная) сила;

Qx, Qy, - поперечные силы;

Мх, Му, - изгибающие моменты;

Mz – крутящий момент.

Учитывая, что деформации тела малы, считают отсечённую часть как бы затвердевшей: это позволяет применять уравнения равновесия для абсолютно твёрдых тел.



.

При сложных нагрузках, действующих на стержень, в его поперечных сечениях могут одновременно возникнуть все шесть компонентов внутренних сил.


В сопротивлении материалов изучение работы стержня под нагрузкой начинается с простейших случаев действия сил.

Если внешние силы, действующие на отсечённую часть стержня, приводятся к равнодействующей, направленной вдоль оси стержня, то в поперечном сечении возникает только нормальная сила N (см. рис 1.2), а остальные внутренние силы будут равны нулю. В таком случае возникает растяжение или сжатие, при котором стержень удлиняется или укорачивается, а его ось остаётся прямой.




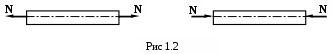
1.6. Понятие о напряжениях в точке

На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению. Выделим в произвольной точке малую площадку(cм. рис. 1.1.) а равнодействующую внутренних сил на этой площадке обозначим R. Отношение



представляет собой среднее напряжение на данной площадке. Если площадку 

уменьшить, то в пределе получим полное напряжение в точке



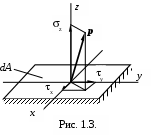
Полное напряжение р может быть разложено на три составляющие по нормали к плоскости сечения и по двум осям в плоскости сечения (см.рис. 1.3.). Проекция вектора полного напряжения р на нормаль обозначается через и называется нормальным напряжением. Составляющие в плоскости сечения называются касательными напряжениями и обозначаются . В зависимости от расположения и наименования осей обозначения и снабжаются системой индексов.




1.7. Связь между напряжениями и внутренними силами


Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA (см. рис. 1.4.) и приложим к ней элементарные силы dA, xdA,ydA.

Суммируя проекции этих элементарных сил, а также их моменты относительно осей Ox, Oy, Oz, найдём;








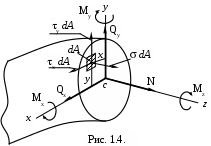
Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению. Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например

N, могут соответствовать различные законы распределения нормальных напряжений по сечению.

Одной из основных задач сопротивления материалов является задача об определении напряжении через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.
1.8. Понятие о деформациях в точке




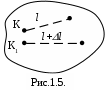
Для определения деформаций в точке К (см. рис. 1.5.) рассмотрим малый отрезок l, исходящий из этой точки в произвольном направлении.

В результате деформации точка К сместится в точку К1 , а отрезок l удлинится на величину l и изменит свое направление.

Предел отношения lim( l / l )=

носит название относительной линейной деформации
в точке К по направлению l. Если в точке К провести три оси, Ох, Оу, Оz, то относительные линейные деформации в направлении этих осей соответственно равны х, у, z.

И 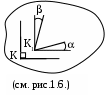зменение первоначального прямого угла в точке К (см. рис. 1.6.) на плоскости  , характеризует угловую деформацию ( или угол сдвига ) в данной точке К.

В малом прямоугольном элементе, вследствие деформации первоначально прямые углы между малыми отрезками dx, dy, dz, исходящими из точки К, изменятся на малые углы ху, хz, уz. Эти изменения прямых углов также называются угловыми деформациями в точке К.

Таким образом, в любой точке имеют место три линейных и три угловых компонента деформации.

Вопросы для самопроверки

  1. Что понимается под задачей курса « Сопротивление материалов»?

  2. Что обеспечивает надежность конструкции?

  3. Что называется деформацией?

  4. Какая деформация называется упругой, какая пластической?

  5. В чем состоит принцип независимого действия сил?

  6. В чем состоит гипотеза плоских сечений?

  7. Какие материалы называются изотропными?

  8. Для чего применяется метод сечений?

  9. Как можно классифицировать внешние силы?

  10. Как можно классифицировать внутренние силы?

  11. Какое напряжение называется полным? Нормальным? Касательным?

  12. Какая связь между напряжениями и внутренними силами?

  13. Что понимается под деформациями в точке?


2. Эпюры внутренних силовых факторов


2.1. Правило знаков при построении эпюр

В инженерной практике особое место занимает умение ясно представить взаимодействие сил в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики - эпюрами. Построение эпюр внутренних силовых факторов носит определённую условность, которая касается как масштаба, так и договорённость о том, какие величины считать положительными или отрицательными, и в какую сторону их откладывать.

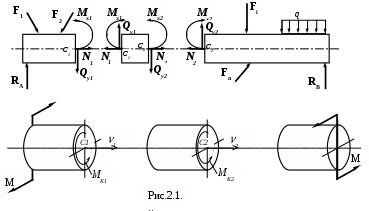
Рассмотрим балку (см. рис. 2.1.), загруженную силами, образующими плоскую систему сил. Для определения внутренних силовых факторов будем использовать метод сечений и уравнения равновесия для отсечённой части, т.е. метод, используемый в ТМ как метод РОЗУ, т.к. будем считать тело абсолютно твёрдым в его деформированном равновесном состоянии.

Установим для внутренних силовых факторов следующее правило знаков:

Продольную силу Nбудем считать положительной, если она вызывает растяжение отсечённой части.

Изгибающий момент МХ будем считать положительным, если он вызывает растяжение нижних волокон.

Поперечную силу QY будем считать положительной, если она стремится повернуть вырезанный из балки элемент бесконечно малой длины по ходу часовой стрелки.

На рисунке 2.1. показаны балка и вал, которые разрезаны на части, на которых действие внутренних силовых факторов показано в положительном направлении.




2.2. Дифференциальные зависимости между M , Q , иq
Изгибающий момент Mx,поперечная сила Qy, интенсивность внешнейнагрузки q связаны между собой определённой зависимостью.


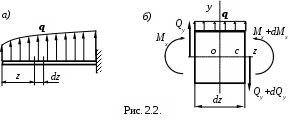
Вырежем из балки, нагруженной распределённой нагрузкой q(z), меняющейся по какому –либо закону (рис. 2.2, а), элемент длиной dz(рис. 2, б).
Нагрузку qсчитают положительной, если она направлена кверху; на протяжении длины

Смотрите также файлы