Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 372
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
р (рис. 12.7).
В этом случае R (радиус цилиндра), т (радиус кривизны образующей цилиндра) и h толщина цилиндра.
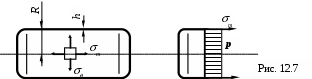
Отсекаем поперечным сечением часть цилиндра и составляем для неё уравнение равновесия
Г
т2 Rh=P.
т2 Rh= R2p.
де сила Р, в независимости от формы днища, будет равна Р= R2p. Тогда,
Таким образом,
тpR/2h.
pR/h,
т.е. окружное напряжение оказываются вдвое большим меридионального. Элемент, выделенный из цилиндрической оболочки, находится в двухосном напряженном состоянии
1 , 2т , 3=0.
По теории Мора, независимо от величины k ,
эквМ=1 - k 3pR/h.
По третьей гипотезе прочности:
эквIII=1 - 3.
Подставляя 1=pR/h и 3 получаем
эквIII= pR/h.
По четвертой гипотезе прочности
эквIV=
 ,
,
т.к. 1 pR/h , 2pR/2h и 30,
то эквIV =0,86 (pR/h).
Разница в результатах получаемых по формулам
эквIII= pR/h и эквIV =0,86 (pR/h), составляет 14%. Рекомендуется применять формулу, основанную на четвертой гипотезе прочности.
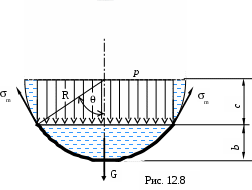
3.Полусфера. Полусферический сосуд (рис.12.8) радиусом R и толщиной h заполнен жидкостью с удельным весом
.
Определить напряжения в сосуде и построить эпюры , т.
Нормальным коническим сечением под углом отсекаем нижнюю часть сферической оболочки и составляем для неё уравнение равновесия
-т 2 Rsin hsin + p ( Rsin)2+ G=0,
G=V=0.3 b2(3R-b),
р - давление на отсечённую часть p=c= R cos,
в=R(1-cos).
Находим: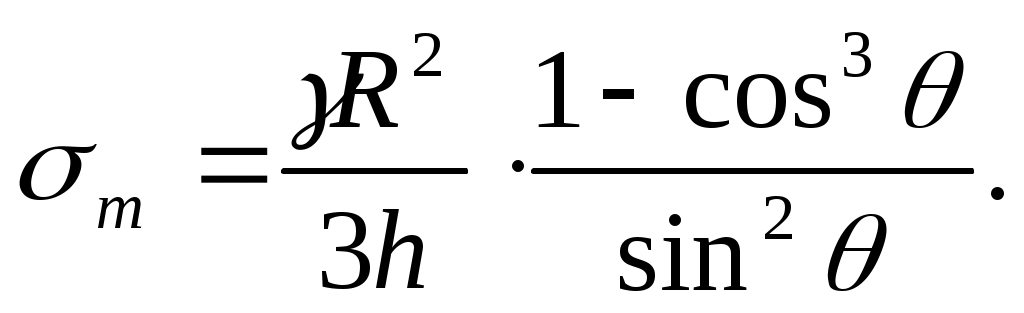
Подставляем в уравнение Лапласа -тнаходим



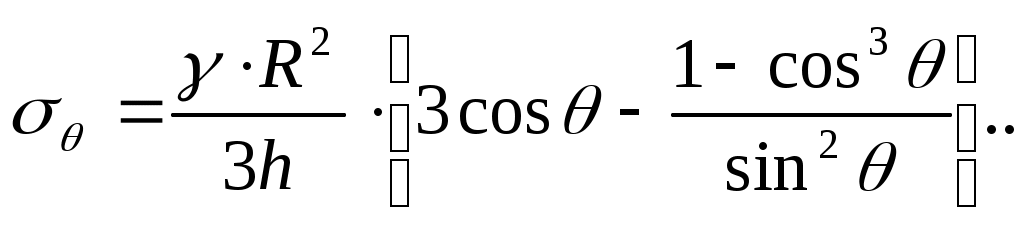
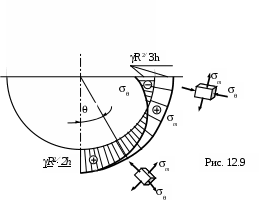
Построим эпюры т и. (12.9).
Напряжения в нижней точке сферы т и. равны. В верхней точкеимеет отрицательное значение.
Там, где т и имеют разные знаки, экв М =т-k.. Тогда расчётное напряжение равно
maxэкв = R2(1+k) 3h,
где по- прежнему k=ТРТС .
Чтобы оболочка не теряла устойчивость от возникающих сжимающих напряжении, её необходимо в этом месте укреплять.
Вопросы для самопроверки
13. Толстостенные цилиндры (трубы)
Цилиндры (трубы) считаются толстостенными, если толщина стенки превосходит 0,1 среднего радиуса, т.е. должно выполняться условие

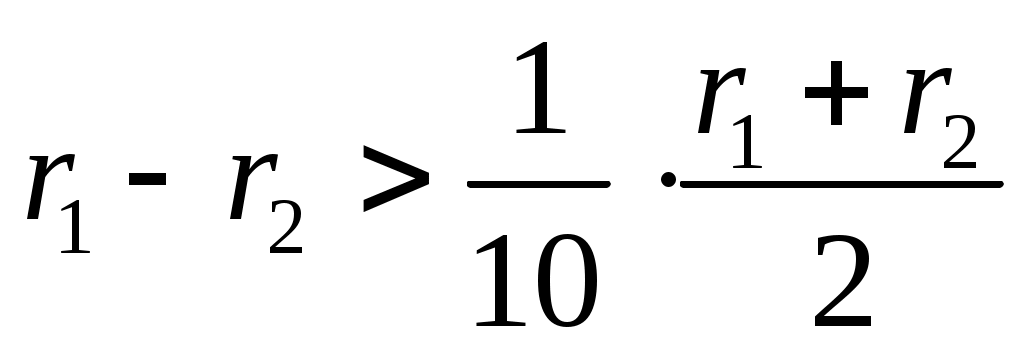 или
или 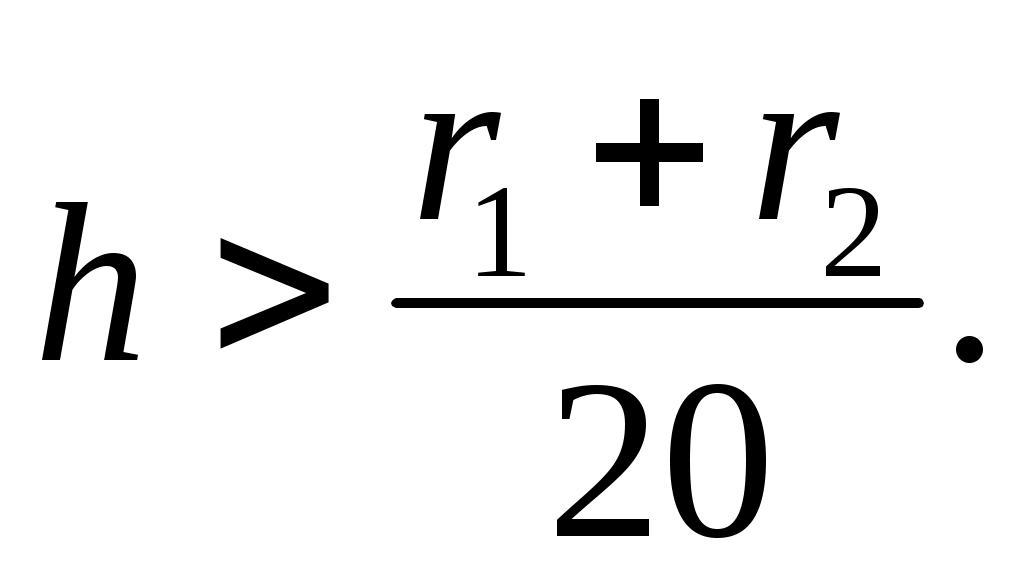
Ограничения задачи:
Утверждения относительно характера деформации:
13.1. Основные уравнения для осесимметричного тела
Рассмотрим цилиндр изображенный на рис 13.1. Двумя сечениями, перпендикулярными к оси цилиндра и находящимися друг от друга на расстоянии, равном единице (рис. 13.1,а), вырежем кольцо (рис. 13.1,б). В этом кольце выделим малый элемент с углом dи цилиндрическими поверхностями с радиусами r иr+dr(рис. 13.1,б,г). Нормальные напряжения на цилиндрической поверхности элемента, имеющей радиус r(радиальные напряжения), обозначим через r; на радиусе r+drнапряжения получат приращения и будут равны r+dr (рис. 13.1,г). Нормальные напряжения плоских боковых гранях (окружные напряжения) обозначим через (рис. 13.1,в,г).
Вследствие осевой симметрии цилиндра и нагрузки касательные напряжения по его граням отсутствуют. Поэтому нормальные напряжения rи будут
главными напряжениями. Так как днищ нет, то нормальные напряжения z=0.
Статическая сторона задачи.
Составим для выделенного элемента (рис. 13.1,б,г) уравнение равновесия проекций всех сил на радиус, получим
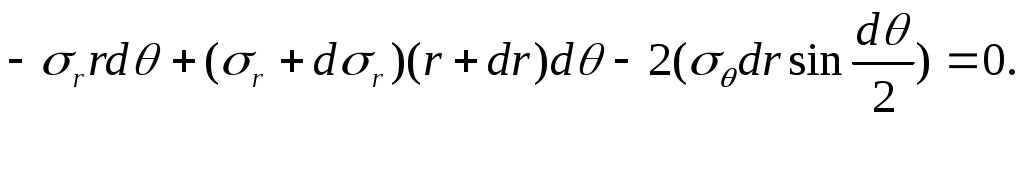
Раскрывая скобки, учитывая малость угла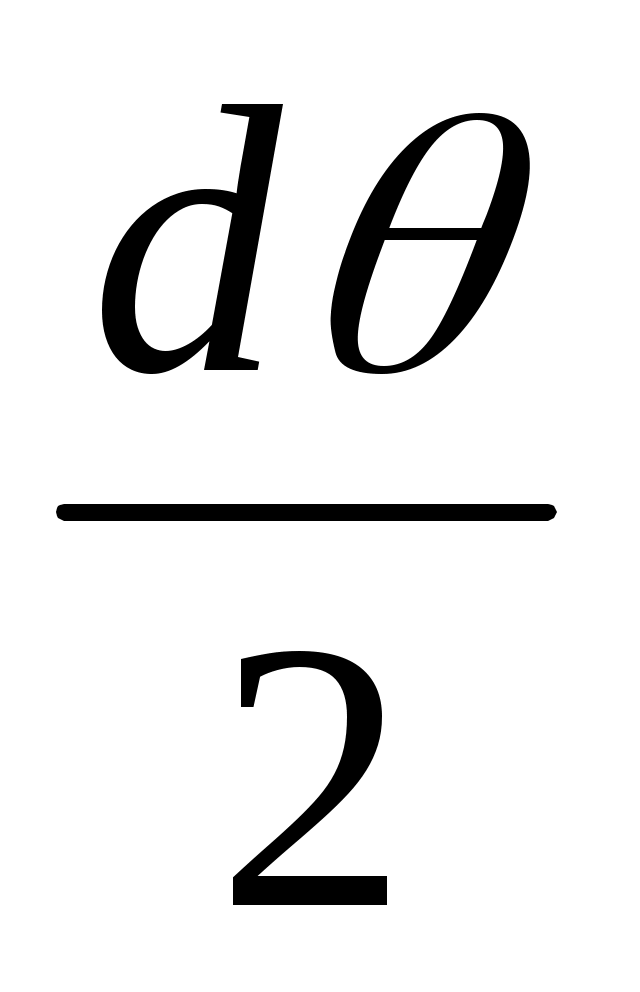 принимаем
принимаем 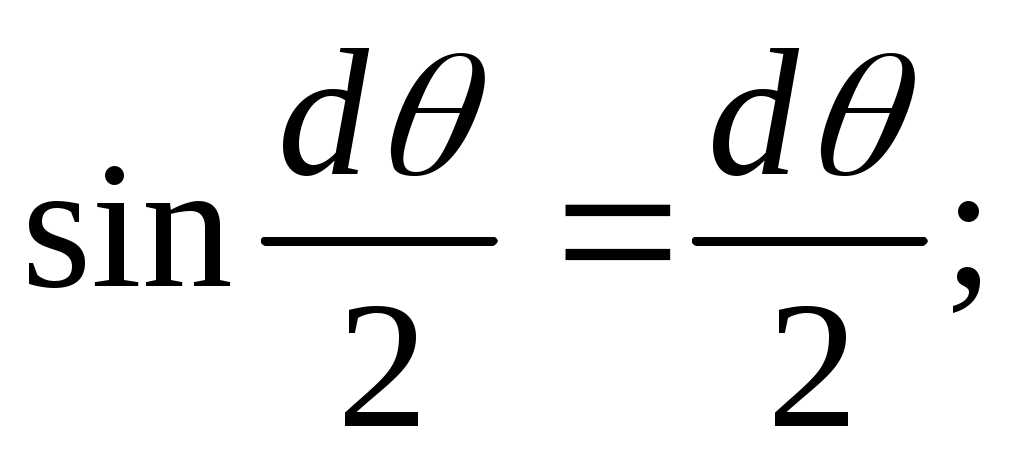 и отбрасывая величины высших порядков малости, получаем
и отбрасывая величины высших порядков малости, получаем
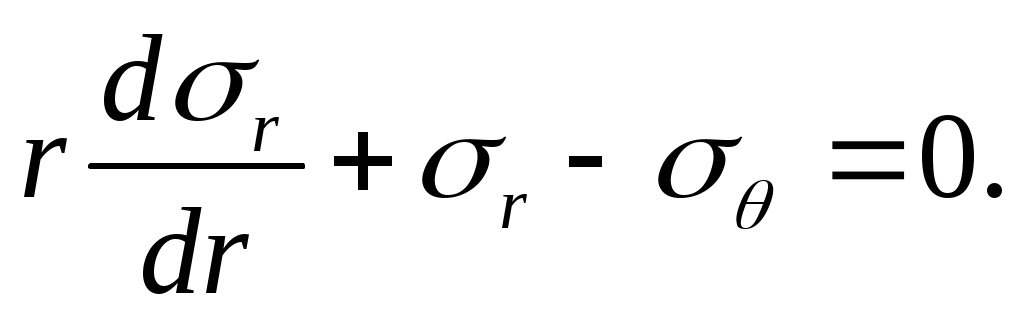 (13.1)
(13.1)
Это уравнение содержит два неизвестных напряжения
rи .
Д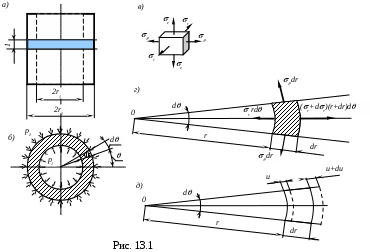
ля их определения, придерживаясь общего плана решения статически
неопределимых задач, рассмотрим ещё геометрическую и физическую стороны задачи.
Геометрическая сторона задачи.
Деформация элемента симметрична относительно оси и поэтому вызовет радиальные перемещения всех точек цилиндра (рис. 13.1,д). Обозначим радиальное перемещение цилиндрической поверхности радиуса r через u, тогда перемещение цилиндрической поверхности радиуса r+dr будет u+du. Абсолютное удлинение элемента длиной dr будет равно du, относительное удлинение
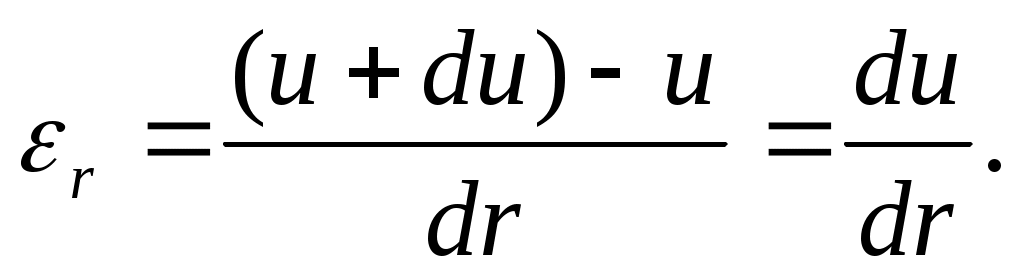 (13.2)
(13.2)
Относительное удлинение в окружном (тангенциальном) направлении на радиусе r
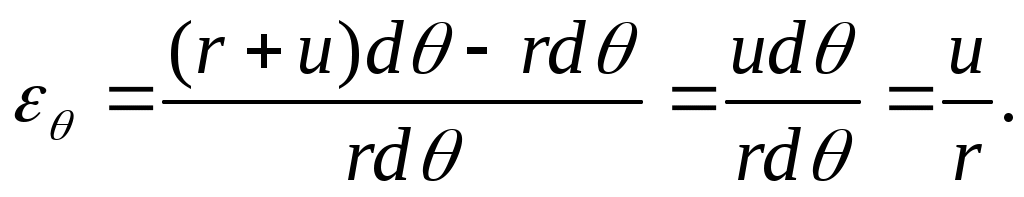 (13.3)
(13.3)
Физическая сторона задачи.
В случае двух стороннего растяжения (z=0, так как днищ нет), которому подвергается рассматриваемый элемент, напряжения и деформации связаны между собой следующими зависимостями:
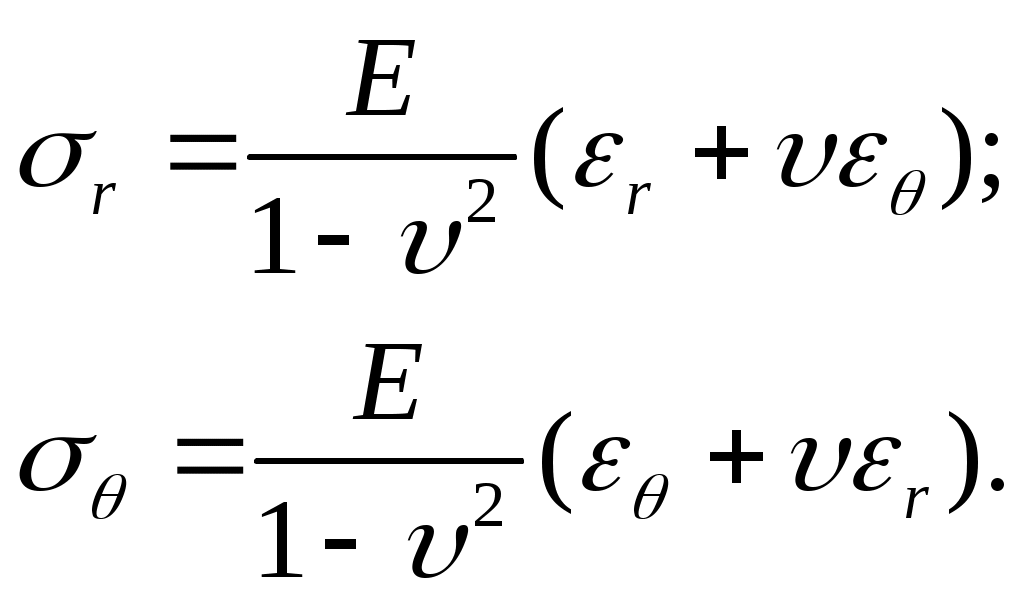

Учитывая (13.2) и (13.3), получим
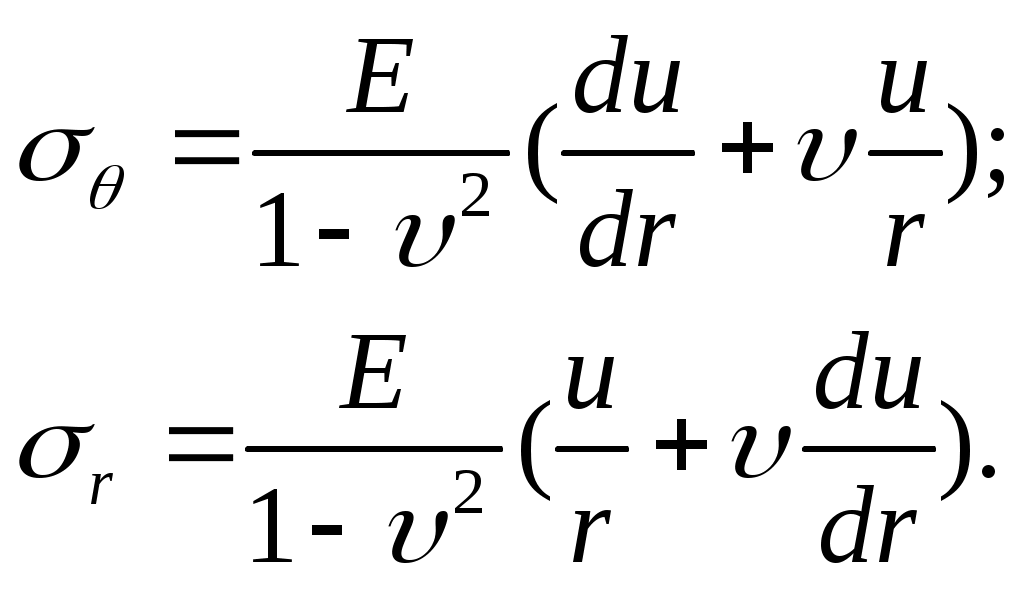
 (13.4)
(13.4)
Синтез.
Подставляя выражение (13.4) в уравнение (13.1), получим для определения перемещения u линейное дифференциальное уравнение второго порядка с переменными коэффициентами
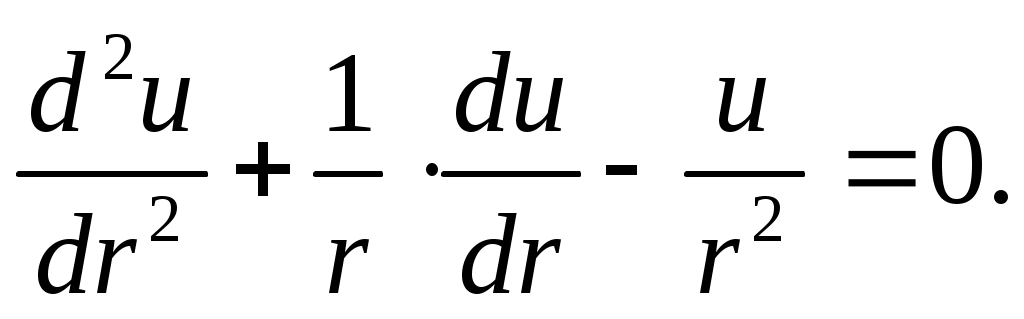 (13.5)
(13.5)
Общее решение этого уравнения в перемещениях имеет вид
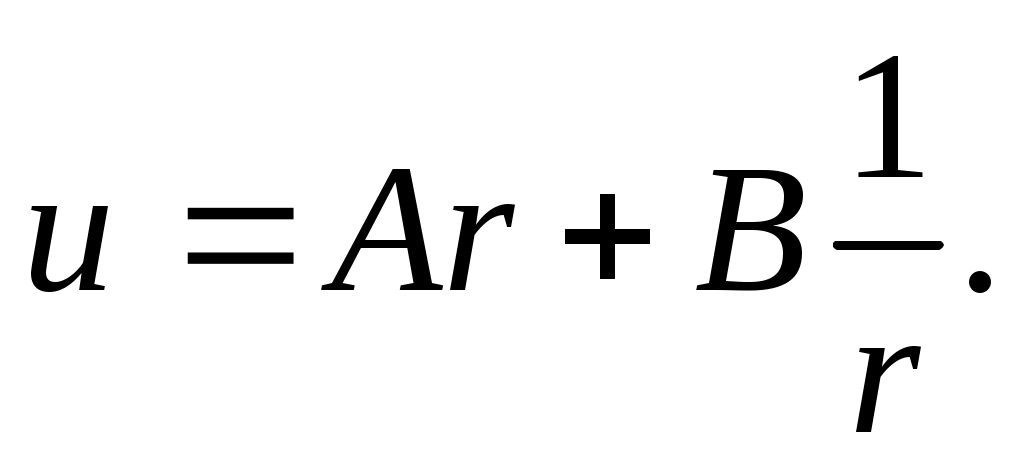 (13.6)
(13.6)
Постоянные интегрирования А и В находятся из условия r на внутренней и наружной поверхностях цилиндра.
Представим уравнение (13.1) в виде
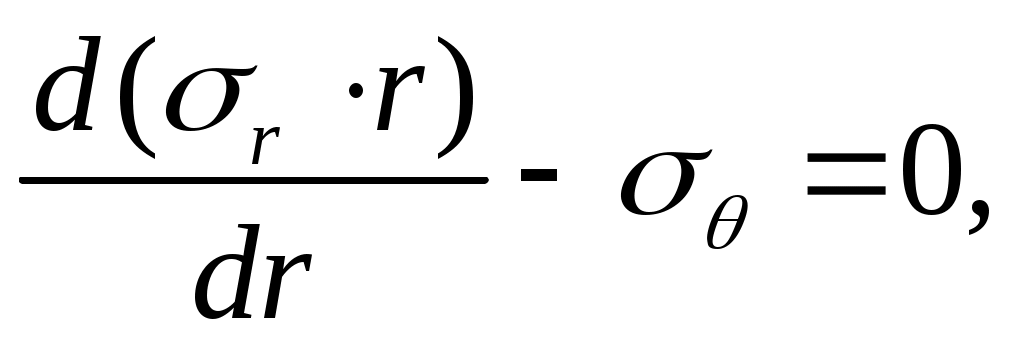 (13.7) тогда
(13.7) тогда
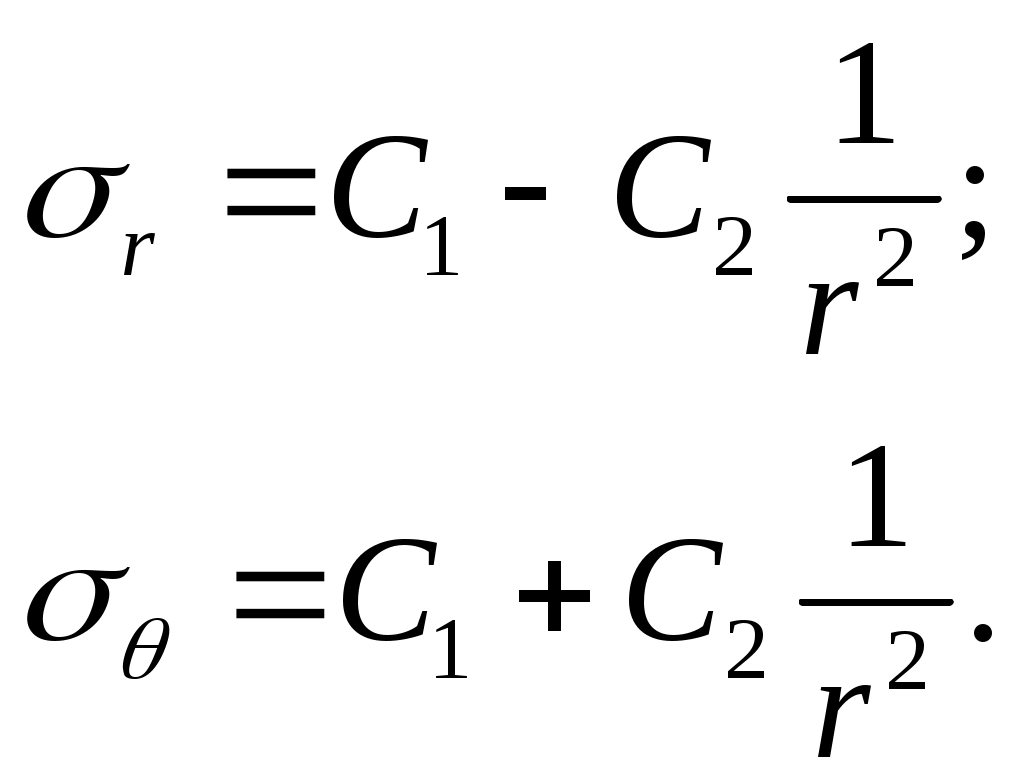
В этом случае R (радиус цилиндра), т (радиус кривизны образующей цилиндра) и h толщина цилиндра.

Отсекаем поперечным сечением часть цилиндра и составляем для неё уравнение равновесия
Г
т2 Rh=P.
т2 Rh= R2p.
де сила Р, в независимости от формы днища, будет равна Р= R2p. Тогда,
Таким образом,
тpR/2h.
Из формулы Лапласа находим
pR/h,
т.е. окружное напряжение оказываются вдвое большим меридионального. Элемент, выделенный из цилиндрической оболочки, находится в двухосном напряженном состоянии
1 , 2т , 3=0.
По теории Мора, независимо от величины k ,
эквМ=1 - k 3pR/h.
По третьей гипотезе прочности:
эквIII=1 - 3.
Подставляя 1=pR/h и 3 получаем
эквIII= pR/h.
По четвертой гипотезе прочности
эквIV=
т.к. 1 pR/h , 2pR/2h и 30,
то эквIV =0,86 (pR/h).
Разница в результатах получаемых по формулам

эквIII= pR/h и эквIV =0,86 (pR/h), составляет 14%. Рекомендуется применять формулу, основанную на четвертой гипотезе прочности.
3.Полусфера. Полусферический сосуд (рис.12.8) радиусом R и толщиной h заполнен жидкостью с удельным весом
.
Определить напряжения в сосуде и построить эпюры , т.
Нормальным коническим сечением под углом отсекаем нижнюю часть сферической оболочки и составляем для неё уравнение равновесия
-т 2 Rsin hsin + p ( Rsin)2+ G=0,
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
G=V=0.3 b2(3R-b),
р - давление на отсечённую часть p=c= R cos,
в=R(1-cos).
Находим:
Подставляем в уравнение Лапласа -тнаходим

Построим эпюры т и. (12.9).
Напряжения в нижней точке сферы т и. равны. В верхней точкеимеет отрицательное значение.
Там, где т и имеют разные знаки, экв М =т-k.. Тогда расчётное напряжение равно
maxэкв = R2(1+k) 3h,
где по- прежнему k=ТРТС .
Чтобы оболочка не теряла устойчивость от возникающих сжимающих напряжении, её необходимо в этом месте укреплять.
Вопросы для самопроверки
-
На каких допущениях построена простейшая теория расчета тонкостенных сосудов и оболочек? -
Как выводится уравнение Лапласа? -
Как проводится расчет на прочность оболочек? -
Каковы особенности расчета сферического провесного днища?
13. Толстостенные цилиндры (трубы)
Цилиндры (трубы) считаются толстостенными, если толщина стенки превосходит 0,1 среднего радиуса, т.е. должно выполняться условие
Ограничения задачи:
-
цилиндр (труба) имеет правильное неизменное круговое сечение и лишен (лишена ) днищ; -
нагрузка, приложенная к цилиндру (трубе), - радиальная и равномерно распределена как по внутренней поверхности цилиндра (трубы) (р1), так и на внешней поверхности (р2).
Утверждения относительно характера деформации:
-
круговая форма цилиндра (трубы ) сохраняется; -
все точки поперечного сечения имеют в своей плоскости только радиальное перемещение; -
точки, лежащие до деформации на одной цилиндрической поверхности, будут и после деформации находиться на одной цилиндрической поверхности.
13.1. Основные уравнения для осесимметричного тела
Рассмотрим цилиндр изображенный на рис 13.1. Двумя сечениями, перпендикулярными к оси цилиндра и находящимися друг от друга на расстоянии, равном единице (рис. 13.1,а), вырежем кольцо (рис. 13.1,б). В этом кольце выделим малый элемент с углом dи цилиндрическими поверхностями с радиусами r иr+dr(рис. 13.1,б,г). Нормальные напряжения на цилиндрической поверхности элемента, имеющей радиус r(радиальные напряжения), обозначим через r; на радиусе r+drнапряжения получат приращения и будут равны r+dr (рис. 13.1,г). Нормальные напряжения плоских боковых гранях (окружные напряжения) обозначим через (рис. 13.1,в,г).
Вследствие осевой симметрии цилиндра и нагрузки касательные напряжения по его граням отсутствуют. Поэтому нормальные напряжения rи будут
главными напряжениями. Так как днищ нет, то нормальные напряжения z=0.
Статическая сторона задачи.
Составим для выделенного элемента (рис. 13.1,б,г) уравнение равновесия проекций всех сил на радиус, получим
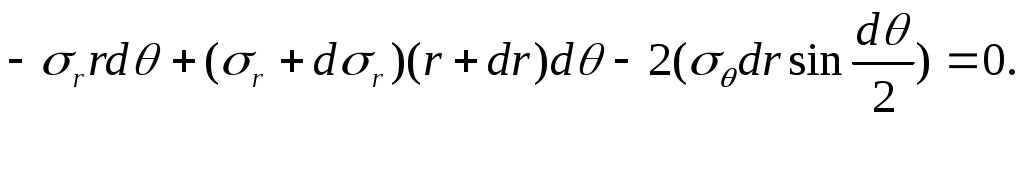
Раскрывая скобки, учитывая малость угла
Это уравнение содержит два неизвестных напряжения
rи .
Д

ля их определения, придерживаясь общего плана решения статически
неопределимых задач, рассмотрим ещё геометрическую и физическую стороны задачи.
Геометрическая сторона задачи.
Деформация элемента симметрична относительно оси и поэтому вызовет радиальные перемещения всех точек цилиндра (рис. 13.1,д). Обозначим радиальное перемещение цилиндрической поверхности радиуса r через u, тогда перемещение цилиндрической поверхности радиуса r+dr будет u+du. Абсолютное удлинение элемента длиной dr будет равно du, относительное удлинение
Относительное удлинение в окружном (тангенциальном) направлении на радиусе r
Физическая сторона задачи.
В случае двух стороннего растяжения (z=0, так как днищ нет), которому подвергается рассматриваемый элемент, напряжения и деформации связаны между собой следующими зависимостями:
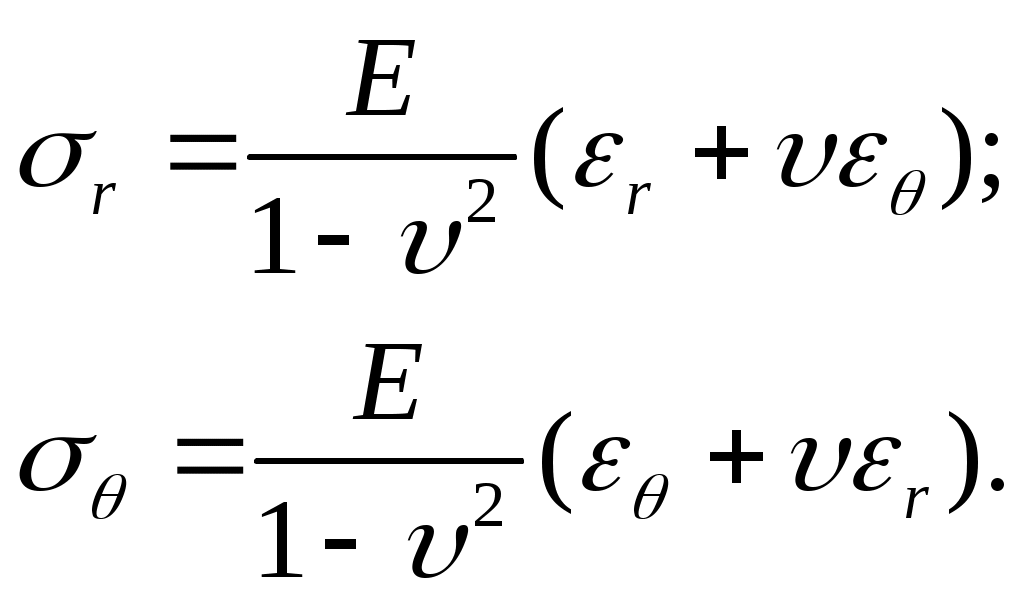
Учитывая (13.2) и (13.3), получим
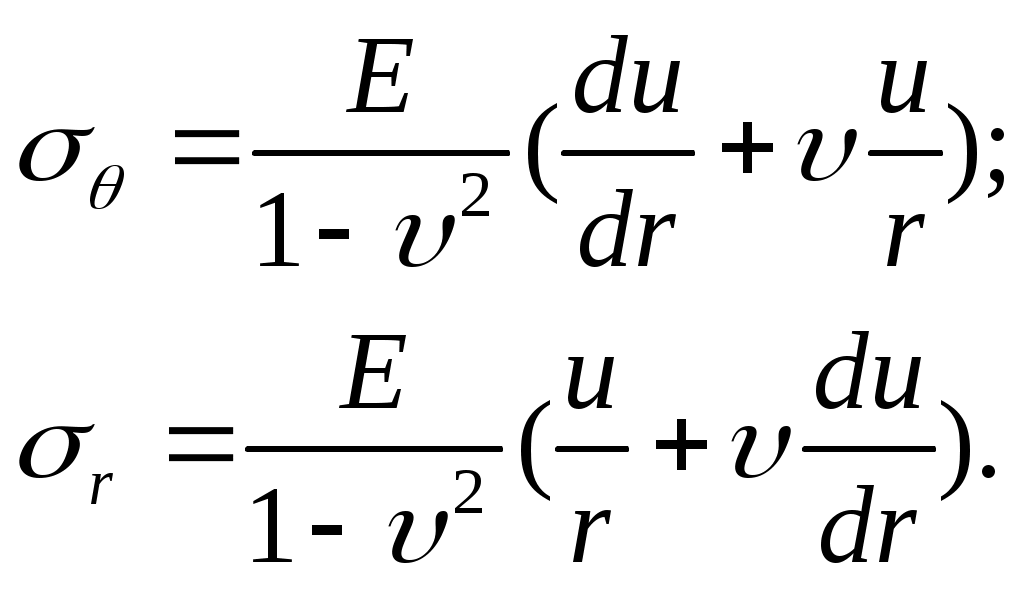
Синтез.
Подставляя выражение (13.4) в уравнение (13.1), получим для определения перемещения u линейное дифференциальное уравнение второго порядка с переменными коэффициентами
Общее решение этого уравнения в перемещениях имеет вид
Постоянные интегрирования А и В находятся из условия r на внутренней и наружной поверхностях цилиндра.
Представим уравнение (13.1) в виде