Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Поэтому для выяснения закона распределение по сечению нормальных напряжений необходимо провести эксперимент. Проведем на боковой поверхности бруса до его нагружения линии, перпендикулярные к оси бруса и имитирующие контур поперечного сечения (рис. 3.2.). При нагружении бруса силой Fэти линии, остаются прямыми и параллельными между собой. Это позволяет считать, что поперечные сечения бруса, плоские до его нагружения, остаются плоскими и при действии нагрузки, что подтверждает гипотезу плоских сечений.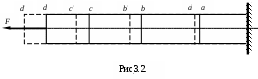


Представим, что брус состоит из бесчисленного множества волокон, параллельныхего оси. Опыт показывает, что линии, перпендикулярные к оси бруса и имитирующие контур поперечного сечения, при растяжении бруса перемещаются, но остаются прямыми и параллельными между собой. Одинаковым удлинениям волокон соответствуют одинаковые напряжения в поперечном сечении всех волокон. Это позволяет в выражении (3.1) вынести величину за знак интеграла. Таким образом,

(3.2)

откуда (3.3)

Итак, в поперечном сечении бруса при центральном растяжении или сжатии (коротких брусьев) возникают равномерно распределенные нормальные напряжения, равные отношению продольной силы к площади поперечного сечения.

При наличии ослабленных сечений бруса (например, отверстиями под заклёпки), следует учитывать фактическую площадь ослабленного сечения A_нетто.

2. 1   2   3   4   5   6   7   8   9   ...   21

---

Понятие о трёх основных задачах сопротивления материалов при центральном растяжении (сжатии) прямого бруса

При расчете условие прочности записывается следующим образом:

(3.4)

Требуется, чтобы наибольшее напряжение в стержне (брусе) не превосходило так называемого допускаемого напряжения, которое обозначается []. Исходя из условия прочности (3.4) можно рассмотреть три задачи, которые называются тремя основными задачами сопротивления материалов.

1. 
   Задача проверки прочности
   

Известно допускаемое напряжение. Известны нагрузка и геометрические размеры конструкции. Определяют _max и проверяют выполняется условие (3.4) или нет.

2. Задача подбора сечения

По известной нагрузке и допускаемому напряжению материала из условия (3.4) определяют (А) для наиболее напряженного элемента конструкции: АN/[].

3.Задача определения допускаемой нагрузки

По известной площади и допускаемому напряжению материала наиболее напряженного элемента конструкции из условия (3.4) определяют допускаемое значение продольной силы (N). Зная (N), определяют допускаемое значение параметра внешней нагрузки, которую может выдержать конструкция:NA[].

ПРИМЕЧАНИЕ

При решении этих задач в неравенстве (3.4) допускаются отклонение в пределах  5%.
3.1.3. Напряжения в наклонных сечениях бруса

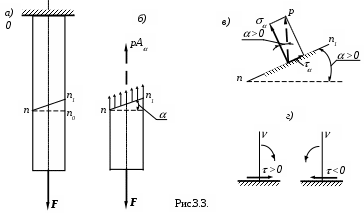
Обозначим  угол между наклонным сечением n-n₁ и поперечным (нормальным) сечением n-n₂ (рис. 3.3,а). Угол - положительный, если нормаль наклонного сечения  повернута на этот угол против часовой стрелки.

Полагая, что напряжения p во всех точках наклонного сечения одинаковы.

Рассмотрим нижнюю часть бруса, отсеченную наклонным сечением n-n₁

(рис. 3. 3, б).

Из условия ее равновесия следует, что напряжения p во всех точках наклонного параллельны оси бруса и направлены в сторону, противоположную силе F, а внутренняя сила pА_, действующая в сечении n-n₁ , равная силе F.

---

Здесь А_- площадь наклонного сечения n-n_{1 ,}равная A/cos (где А – площадь поперечного сечения n-n₀ ).

Следовательно, F= p А_{ ,}(3.5)

откуда p= F/ А_= Fcos/ А=cos_,

где F/ А =  - нормальные напряжения в поперечных сечениях бруса.

Разложим напряжение р на две составляющих напряжения: нормальное _{ ,} перпендикулярное к плоскости сечения n-n_{1 ,} и касательное_, параллельное этой плоскости (рис. 3.3,в).

Тогда:

_=р cos= cos ²; (3.6) _= p sin = sin cos=(/2)sin2. (3.7)

При пользовании как формулами (3.6) и (3.7), так и формулами, приведенными ниже, придерживаются следующих правил знаков: растягивающие нормальные напряжения считают положительными; касательные напряжения считают положительными, если внешнюю нормаль к площадке его действия надо повернуть на 90⁰ по часовой стрелке для того, чтобы её направление совпало с направлением (рис. 3.3, г).

Из формулы (3.7) следует, что касательные напряжения при =±45⁰имеют экстремальные значения _max= /2.

Значение _=0 при =0 (т.е. в поперечных сечениях бруса) и при =90⁰.

Таким образом, на площадках с экстремальными нормальными напряжениями касательные напряжения равны нулю.

3.1.4. Закон парности касательных напряжений

Определим значения касательных напряжений _1 и_2 в двух наклонных сечениях, перпендикулярных друг к другу (рис. 3.4.).

Углы ₁ и ₂ наклона этих сечений к плоскости поперечного сечения бруса находятся в зависимости ₂ = ₁- 90⁰.

---

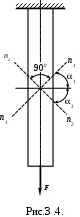
По формуле (3.7)

_2 = ( /2)sin2(₁- 90⁰)= -( /2)sin(180⁰-2₁)= = -( /2)sin2₁ = -_1. (3.8)

Таким образом, имеем закон парности касательных напряжений: касательные напряжения в двух взаимно перпендикулярных площадках равны друг другу по величине и обратные по знаку (см. рис. 3.5, а, б ).




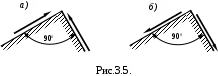
3.2.1. Продольные деформации. Закон Гука

Рассмотрим прямой брус постоянного сечения длиной l, заделанный одним концом и нагруженный на другом конце растягивающей силой F (рис. 3.6.). По действием силы F брус удлиняется на некоторую l, которая называется полным, или абсолютным, линейным удлинением. Если повторим опыты с брусьями из того же материала, но с иной площадью поперечного сечения, то увидим, что удлинения меняются обратно пропорционально площади.

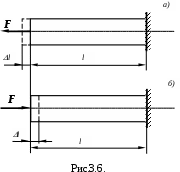Опыты приводят к заключению, что пока нагрузка на образец не достигла известного предела, удлинение прямо пропорционально

силе F, длине образца l и обратно пропорционально площади А.

Опытные данные позволяют записать формулу, которая носит название закона Гука:

(3.9) (9)

где Е коэффициент пропорциональности, зависящий от материала называемый модулем продольной упругости или модулем упругости первого рода (модулем Юнга I-го рода).
Величина ЕА называется жёсткостью бруса (стержня) при растяжении и сжатии.

Зависимость (3.9) можно представить в ином виде. отношение l/l называется относительным удлинением.

Подставив в предыдущую формулу вместо l/lвеличину, а вместо F/A – величину нормального напряжения , получаем иное выражение Закона Гука.

(3.10)

или

---

. (3.11)
3.2.2. Поперечная деформация

Кроме продольной деформации, при действии на брус сжимающей или растягивающей силы наблюдается также поперечная деформация. При сжатии бруса его поперечные размеры увеличиваются, а при растяжении – уменьшаются. Если поперечный размер бруса до приложения к нему сжимающих сил Fобозначить b, а после приложения этих сил b+b(рис. 3.7.), то величина b будет обозначать абс
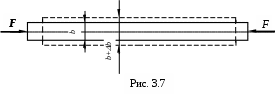
олютную поперечную деформацию брус.

Отношение ^b/bявляется относительной поперечной деформацией.

Опыт показывает, что при напряжениях, не превышающих предела упругости относительная поперечная деформация ^прямо пропорциональна относительной продольной деформации , но имеет обратный знак:

^(3.12)

Коэффициент пропорциональности зависит от материала бруса. Он называется коэффициентом поперечной деформации, или коэффициентом Пуассона, и представляет собой отношение относительной поперечной деформации к продольной, взятое по абсолютной величине, т.е.

^ /. (3.13)

Коэффициент Пуассона наряду с модулем упругости Е характеризует упругие свойства материала и определяется экспериментально. Для различных материалов он изменяется от нуля (для пробки) до 0,5 (для резины, парафина).

Для всех металлов числовые значения лежат в пределах 0,25 – 0,35.

3. 
   Деформация и напряжения при действии собственного веса
   

При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придётся учесть, что относительное удлинение различных участков стержня будут переменными, как и напряжения.

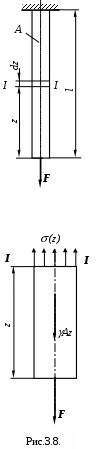Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка dz (см. рис. 3.8.).

Абсолютное удлинение этого участка равно



Полное удлинение стержня lравно

---