Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 375

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Деформация, остающаяся в теле после разгрузки, получила названиеостаточной или пластичной, а способность тела приобретать пластическую деформацию – пластичность.

Сплошность

7.1.1. Общие замечания

Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу

Методика расчёта

Нагрузка, при которой прямолинейная форма перестаёт быть формой устойчивого равновесия, называется критической(Fкр ). Таким образом, исследование устойчивости стержня заключается в определении Fкр. Для обеспечения устойчивости допускаются нагрузки, составляющие лишь часть критических. Отношение критической нагрузки Fкр к её допускаемой величине ([F]y) называется коэффициентом устойчивости: (11.1)Коэффициент ny зависит от материала стержня. Его рекомендуемые величины находятся в пределах: для стальных стоек 1.5…3; для деревянных 2.5…3.5; для чугунных 4.5…5.5. Метод Эйлера для определения критической силы. Формула Эйлера.Для исследования устойчивости равновесия упругих систем имеется несколько методов: метод малых колебаний, энергетический метод и др. В инженерной практике для невесомых стержней с нагрузкой, приложенной точно в центре тяжести торцовых сечений и параллельно продольной оси стержня используют более простой метод – метод Эйлера.Метод Эйлера основан на анализе разветвления форм равновесия упругой системы. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма. Для вывода формулы Эйлера рассмотрим шарнирно - опёртый, центрально - сжатый стержень постоянного сечения (рис. 11. 3) в слегка отклонённом состоянии от прямолинейной формы.Изгибающий момент в произвольном сечении равенF (11.2)Дифференциальное уравнение изгиба стержня запишется в виде: (11.3)или (11.4)где (11.5)Интеграл дифференциального уравнения (11.4) имеет вид (11.6)Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z=0 и Следовательно, уравнение оси изогнутого бруса (6) примет вид (11.7)Таким образом, стержень изгибается по синусоиде.Второе граничное условие: при z=l и  Bsinkl=0Это условие выполняется в двух случаях:1) В=0; 2) sinkl=0Первый случай нас не интересует, так как при В=0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.Второе условие sinkl=0 дает kl= 2 3 nучтя значение k (11.5), получим: Итак, получено не одно, а множество значений критической силы. Каждой критической силе соответствует своя форма равновесия (рис. 11.4). Подставляя найденное значение k в уравнение оси изогнутого бруса (11.7), замечаем, что при первой критической силе стержень изгибается по одной полуволне синусоиды, а при всех последующих число полуволн равно номеру соответствующей критической силы. Равновесие, соответствующее первой форме изгиба, является устойчивым, а все всем остальным – неустойчивым.Для инженерных расчетов практический интерес представляет только наименьшая критическая сила (11.8)Эту формулу в 1744 г. впервые получил Леонард Эйлер, поэтому она называется формулой Эйлера, а определяемую этой формулой критическую силу – эйлеровой силой.Из формулы (11.8) видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.Таким образом, выясняется резкая разница между работой стержня на растяжение и на сжатие. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и поэтому различна для разных сортов стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина. Предельная растягивающая сила не зависит от длины стержня, в то время как при сжатии она быстро падает с увеличением длины.Продольный изгиб сжатых стержней особенно опасен потому, что он наступает внезапно, и поэтому его трудно предупредить. В растянутых стержнях признаки опасного состояния часто наступают задолго до разрушения, а в сжатых стержнях каких- либо заметных признаков потери устойчивости, как правило, установить не удается.11.3. Влияние способов закрепления концов стержня на величинукритической силыНа рис. 11.5 показаны различные случаи закрепления концов сжатого стержня. Для каждого случая необходимо проводить свое решение аналогичное тому, что сделано в предыдущем параграфе для шарнирно опертого стержня. Эти решения показывают, что для всех случаев, изображенных на рис. 11.5, критическую силу можно представить в виде формулы: (11.9)где   коэффициент приведения длины, а величина ll0называется приведенной (свободной) длиной. Понятие о приведенной длине было впервые введено профессором Петербургского института путей сообщения Ф.С. Ясинским (1892).Свободная длина l0может быть истолкована как некоторая условная длина шарнирно опертого стержня, имеющего такую же критическую силу, как заданный стержень. В отдельных случаях это положение вытекает из чисто геометрического толкования (длина полуволны синусоды). Так, например, если стержень заделан одним концом, рассматривать как половину стержня, шарнирно опертого по концам, то l0= 2l. Следовательно, =2.Для стержня, заделанного двумя концами, длина полуволны, замеренная между двумя точками перегиба, где Мх=0,составит половину длины стержня, следовательно, для этого случая =0,5. 11.4. Пределы применимости формулы Эйлера. Формула Ясинского Формула Эйлера, полученная более 267 лет назад, долгое время являлась предметом дискуссий. Формула Эйлера для некоторых случаев не подтверждалась экспериментами. Объясняется это тем, что формула Эйлера выводилась в предположении, что при любом значении силы стержень работает в пределах упругих деформаций с использованием закона Гука. По этому формулу Эйлера нельзя применять в случаях, когда критические напряжения больше предела пропорциональности. Для установления предела применимости формулы Эйлера найдем Здесь радиус инерции. Обозначим через  Величина  называется гибкостью стержня.Итак, (11.10) Это так же формула Эйлера, но записанная для критического напряжения, а не для критической силы. Принято изображать уравнение (11.10) в координатах кр -(рис. 11.6). Полученную кривую часто называют гиперболой Эйлера. Как видно из уравнения (11.10), при малых гибкостях критические напряжения могут значительно превосходить предел прочности материала. Действительно короткие и толстые стержни (например, кубы, имеющие гибкость 

Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.

Так как

Отсюда определяется меридиональное напряжение т.

Напряженное состояние является двухосным

Из формулы Лапласа находим

где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки

15. Динамическое действие нагрузок

15. Динамическое действие нагрузок…………………………………..216


1 = - 3 = таx = - тin= MK/ W . (6.11)
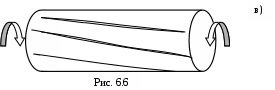
Экспериментальные данные свидетельствуют о правильности сделанных выводов. Так, например, скручиваемый чугунный вал разрушается по винтовой поверхности от действия главных растягивающих напряжений (рис.6.6, а)). Вал, изготовленный из пластичной стали, разрушается по поперечному сечению в виде среза (рис. 6.6, б)), т. к. растягивающие напряжения для стали менее опасны, т. к. они действуют по большей наклонной площади. При разрушении деревянного стержня (рис. 6.6, в)) происходит скалывание вдоль волокон, что свидетельствует о наличии касательных напряжений в его продольных плоскостях, а прочность д

ревесины в этом направлении меньше, чем поперёк волокон.




    1. Расчёт бруса круглого поперечного сечения на прочность и

жёсткость при кручении
При расчёте скручиваемых валов на прочность и жёсткость, возможны три вида задач:

а) проверка напряжений или деформаций (проверочный расчёт);

б) подбор сечения (проектный расчёт);

в) определение допускаемой нагрузки.

При решении этих задач в неравенствах (6.12) и (6.13) допускается отклонение в пределах 
Наибольшие касательные напряжения, возникающие в скручиваемом брусе, не должны превышать соответствующих допускаемых напряжений:

max=( MK max )/ W . (6.12)
Это требование называется условием прочности при кручении.
Практически в зависимости от материала и условий работы для стальных валов принимают 20 40 МПа.

При проверке напряжений следует построить эпюру МК, которая облегчает определить опасное сечение бруса. Затем определяют max опасного сечения и сравнивают его с . Если условие (12) не удовлетворяется, то требуется изменить размеры сечения бруса, или уменьшить действующую нагрузку, или применить материал высокой прочности.

При подборе сечения по заданной нагрузке определяют крутящие моменты в поперечных сечениях бруса (обычно строится эпюра МК), а затем по формуле (12) определяется полярный момент сопротивления сечения для каждого участка


WiMKimax / [].

По формулам для сплошного сечения Wr3d3 16 идля кольцевого сечения W(D3 16) (1-4 ) определяются диаметры вала.

При определении допускаемой нагрузки с помощью формулы (12) по известному [] и полярному моменту сопротивления сечения W определяется допускаемый крутящий момент MKmax, а затем устанавливаются допускаемые внешние нагрузки.

Расчёт вала на прочность не исключает возможности возникновения деформаций, недопустимых при его эксплуатации. Поэтому в необходимых случаях валы рассчитываются не только на прочность, но и на жёсткость.

Условие жёсткости бруса при кручении имеет вид

max, (6.13)

где max – наибольший относительный угол закручивания бруса, определяемый по формуле (6.8);  - допускаемый относительный угол закручивания, для разных конструкций равный от 0.000026 до 0.00035 рад на 1 см длины вала.

Из условия (6.13) можно решить три задачи, как и из условия (12): проверочный расчёт, подбор сечения и определение допускаемой нагрузки.


    1. Кручение прямого стержня некруглого поперечного сечения


Задача кручения стержней с некруглым поперечным сечением является сложной по сравнению с задачей кручения круглого стержня. Допущения, принятые для круглого стержня здесь не применимы. Отдельные точки сечения перемещаются вдоль оси стержня, и все сечение в целом перестает быть плоским. Происходит так называемая депланация (коробление) сечения.

Н
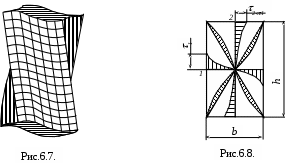
а рис. 6.7. показана депланация прямоугольных поперечных сечений скручиваемого стержня. Точное решение для некоторых типов поперечного сечения дается в теории упругости. Ограничимся приведением окончательного результата для стержня прямоугольного сечения. На рис.6.8. показано прямоугольное сечение, на котором изображены эпюры касательных напряжений по главным осям сечения и по диагоналям. В угловой точке напряжения равны нулю. Наибольшее напряжение развивается в середине длинной стороны

( в точке 1). Его можно определить по формуле

(6.14)

где

Через выражается напряжение в середине короткой стороны , а угол закручивания определяется по формуле

(6.15)

где I=b4.

Входящие в эти формулы коэффициенты , , зависят от соотношения сторон прямоугольника m=h/b/. Для некоторых значений mвеличины , и даются в таблице.


m






1

1,5

2,0

3,0
0,140

0,294

0,457

0,790
0,208

0,346

0,493

0,801
1,0

0,859

0,795

0,753

Вопросы для самопроверки


  1. Какие напряжения возникают в поперечном сечении круглого стержня при кручении?

  2. Как находится их величина в произвольной точке поперечного сечения?

  3. Возникают ли при кручении нормальные напряжения?

  4. Чему равен момент сопротивления кольцевого сечения?

  5. Как вычисляется величина угла закручивания?

  6. Как производится расчет вала на прочность?

  7. Как производится расчет вала на жесткость?

  8. Как находятся максимальные напряжения при кручении стержня прямоугольного сечения?

  9. Чему равен пластический момент сопротивления сечения при кручении?


7. Изгиб прямых стержней
0>

7.1.1. Общие замечания


Изгиб представляет собой такую деформацию, при которой ось стержня и его продольные волокна изменяют свою кривизну. В случае, когда все действующие на стержень силы, в том числе и опорные реакции, лежат в одной из главных плоскостей инерции, и изогнутая ось также лежит в этой плоскости, то изгиб называют плоским.

Частный случай изгиба, при котором в поперечных сечениях стержня возникает только один внутренний силовой фактор – изгибающий момент, называется чистым изгибом.

В общем случае изгиб называется поперечным.

Стержни, работающие преимущественно на изгиб, принято называть балками.
7.1.2. Чистый изгиб

П
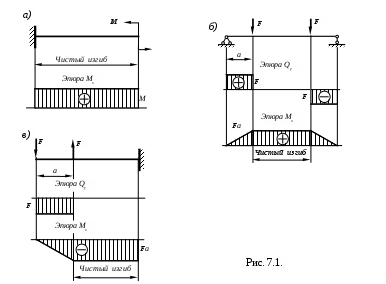
ри чистом изгибе в балке возникают только изгибающие моменты Mx, а Qy=0. Рассмотрим наиболее простые случаи изгиба. Некоторые примеры показаны на рисунке 7.1.



    1. 7.1.3. Нормальные напряжения при чистом изгибе


Изучение напряженного состояния при изгибе удобнее начинать со случая, когда поперечная сила (Qy=0 ) равна нулю, т.е. с чистого изгиба.

На участках чистого изгиба в любом сечении возникает один и тот же изгибающий момент(Mx), который определяется зависимостью

. (7.1)

Однако этого уравнения статики недостаточно для определения нормального напряжения, так как неизвестно его изменение по y, да начало отсчета для y также неизвестно, т.е неизвестен закон изменения нормального напряжения по сечению. Необходимо к условию статики привлечь условия деформации, которые можно сформулировать только на основании экспериментальных наблюдений.

Р 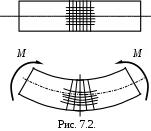ассмотрим брус с поперечным сечением, имеющим хотя бы одну ось симметрии, которая совпадает с силовой плоскостью. Если на боковую плоскость бруса нанести ортогональную сетку (рис. 7.2. ), то окажется, что, после того как произойдёт деформация изгиба, продольные линии примут криволинейное очертания, а поперечные линии останутся прямыми, но примут радиальное направление. Это обстоятельство показывает, что при изгибе, так же как и при растяжении, справедлива
гипотеза плоских сечений: поперечное сечение, плоское до деформации, остается плоским и после деформации. Данная гипотеза вместе с уравнениями статики позволяют решить задачу об определении напряжений при чистом изгибе.
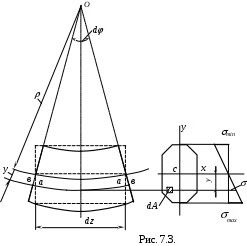
Рассмотрим элемент бруса длиной dz, который после деформации искривится (рис. 7.3). Два смежных сечения наклонятся, образовав между собой угол d .При этих условиях верхние волокна будут сжиматься, а нижние – растягиваться. Можно найти и такие волокна, длина которых при изгибе остается неизменной, назовем их нейтральными. Совокупность волокон, не меняющих своей длины при изгибе балки, называется нейтральным слоем. На поперечном сечении нейтральный слой, образуют след – нейтральную линию Сх. Радиус кривизны нейтрального волокна обозначим . По чертежу (рис. 7.3) легко установить, что удлинение волокна аа, отстоящего на расстоянии у от нейтрального слоя, состоит из двух дуг ав, каждая из которых равна величине у(d /2). Таким образом, общее удлинение произвольного волокна равно

dz = yd.

Но так как dz = d, то относительное удлинение этого волокна


Если предположить, что отдельные волокна при изгибе не давят друг на друга, то каждое из них будет находиться в условиях простого растяжения ( или сжатия).

В этом случае для перехода от удлинения напряжениям можно воспользоваться законом Гука

(7.2)

Прежде всего установим положение нейтральной линии, от которой отмеряется расстояние у. Для этого воспользуемся тем, что равнодействующая элементарных нормальных сил dAв поперечном сечении при чистом изгибе равна нулю:

(7.3)

или



Так как то

Смотрите также файлы