Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 373
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
– ось симметрии), по формуле (17.12) получим, что независимо от угла для осей, проходящих через точку А, 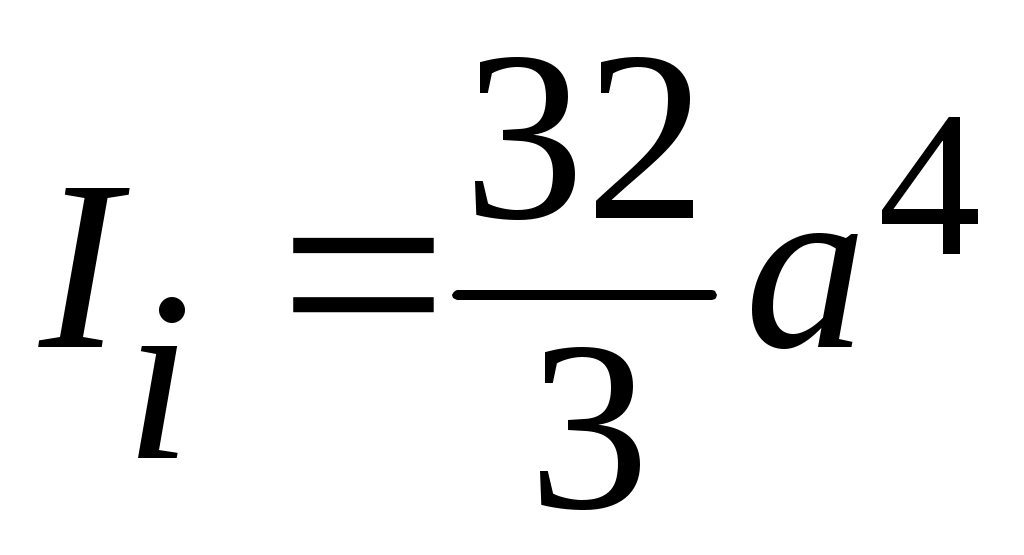 .
.
К геометрическим характеристикам плоских сечений относятся также неинтегральные характеристики:
радиус инерции сечения относительно центральных осей
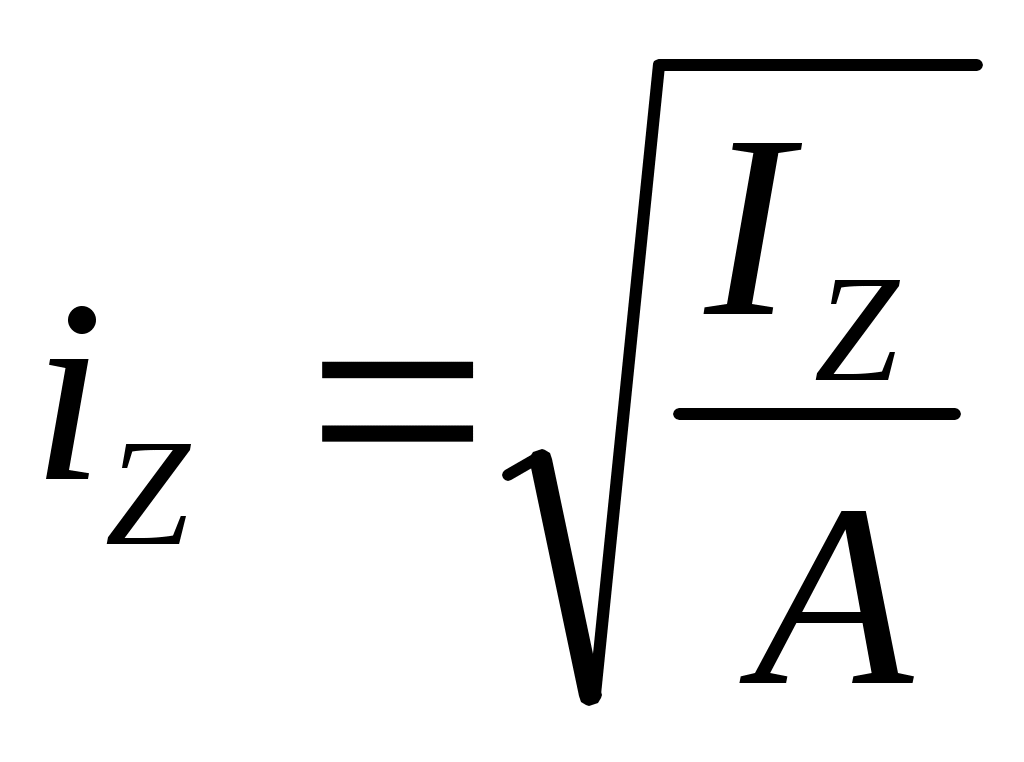 > 0,
> 0, 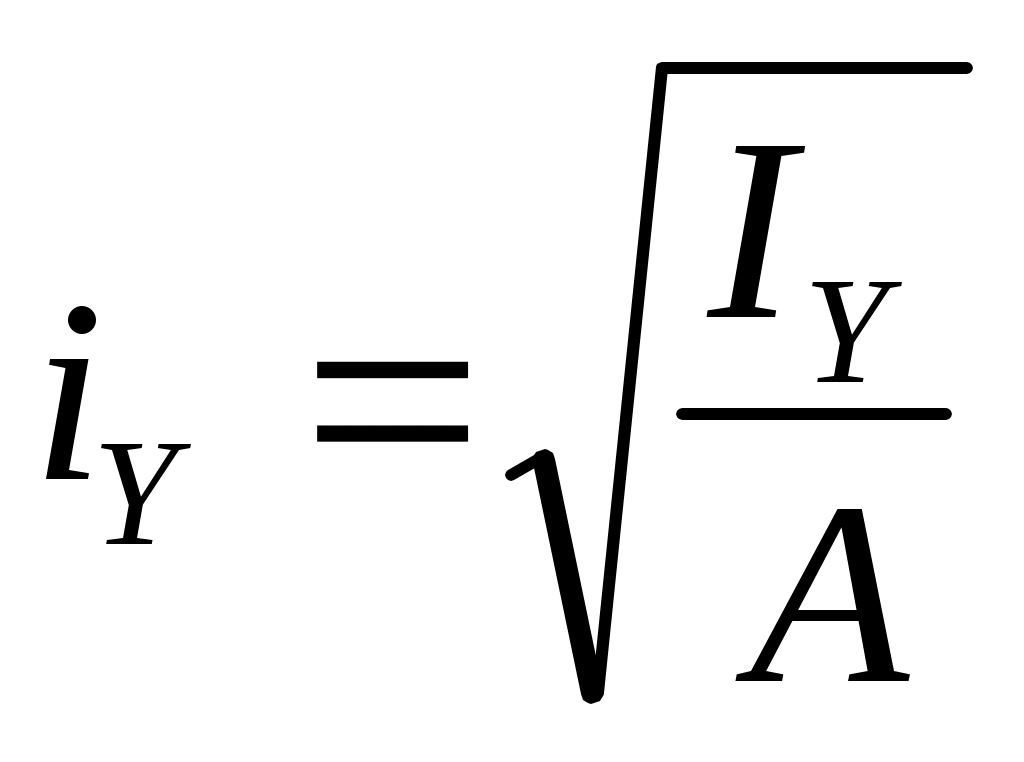 >0, [м]; (17.17)
>0, [м]; (17.17)
осевые моменты сопротивления сечения относительно главных центральных осей
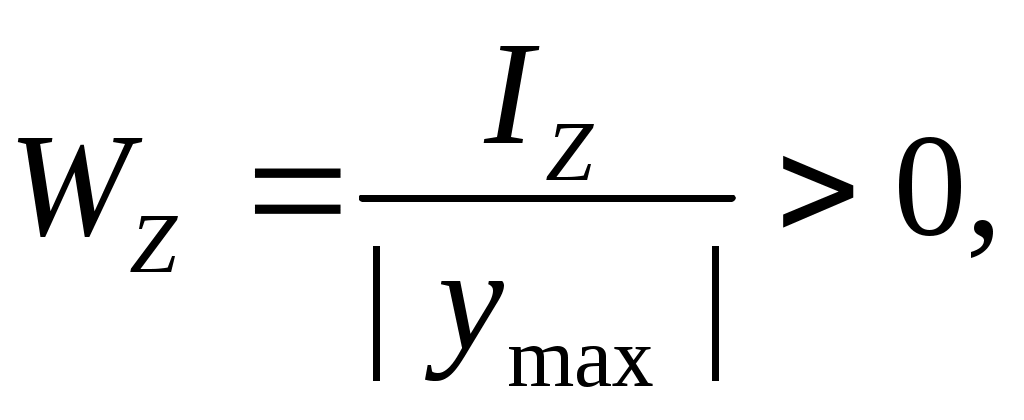 [м3], (17.18)
[м3], (17.18)
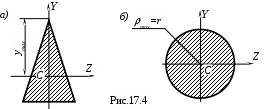
где ymax – ордината наиболее удаленных от оси Z точек сечения (рис.17.4,а,б);
полярный момент сопротивления круглого сечения
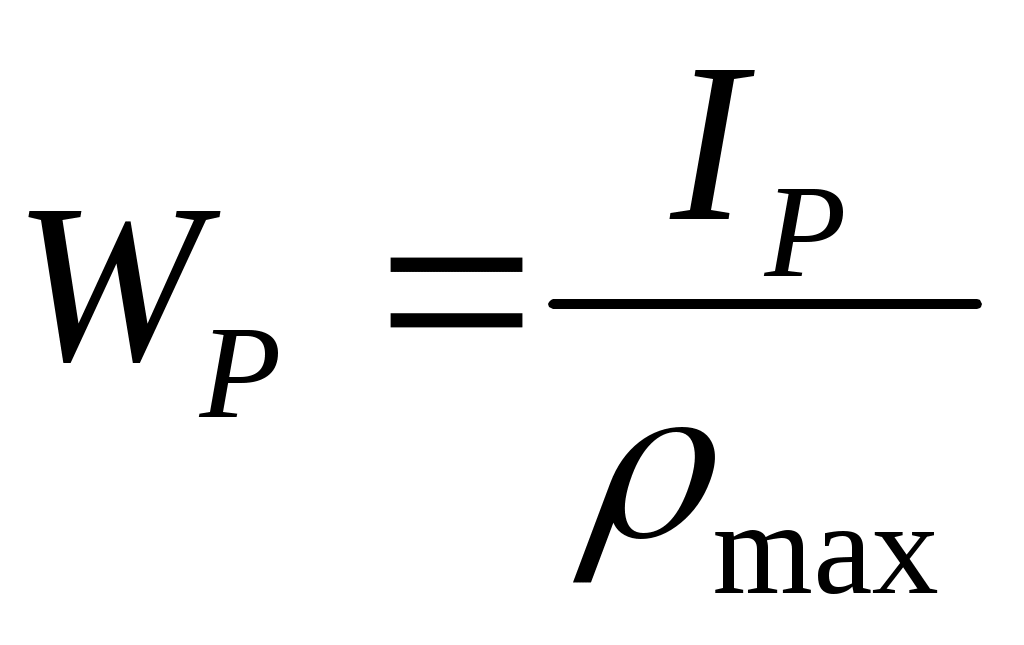 > 0, [м3], (17.19)
> 0, [м3], (17.19)
где max=r– расстояние до наиболее удаленной точки от центра круглого сечения.
Учитывая свойство аддитивности геометрических характеристик, во многих задачах при их решении удобно достроить заданное сечение до такой простой фигуры, для которой геометрические характеристики известны.
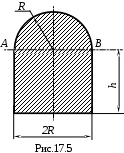
Пример 1. Определить величину размера h для фигуры (рис.17.5), при котором центр тяжести её будет находиться на прямой АВ
(R –задан).
Решение
 Для того чтобы центр тяжести находился на прямой АВ, последняя должна совпадать с центральной осью ZC. Следовательно статический момент всей площади фигуры
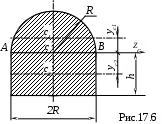
Для того чтобы центр тяжести находился на прямой АВ, последняя должна совпадать с центральной осью ZC. Следовательно статический момент всей площади фигуры 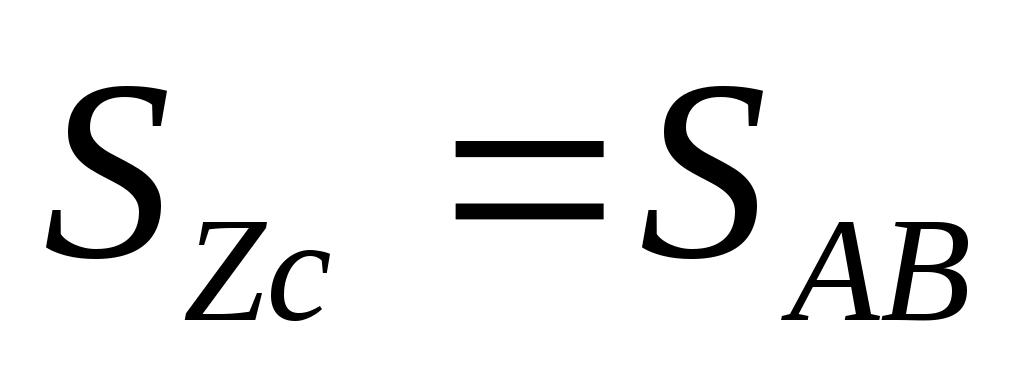 должен быть равен нулю. Тогда, для фигуры (рис.17.6), состоящей из двух частей 1 и 2 :
должен быть равен нулю. Тогда, для фигуры (рис.17.6), состоящей из двух частей 1 и 2 : 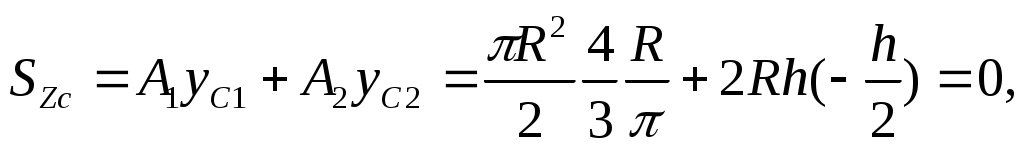 Откуда
Откуда 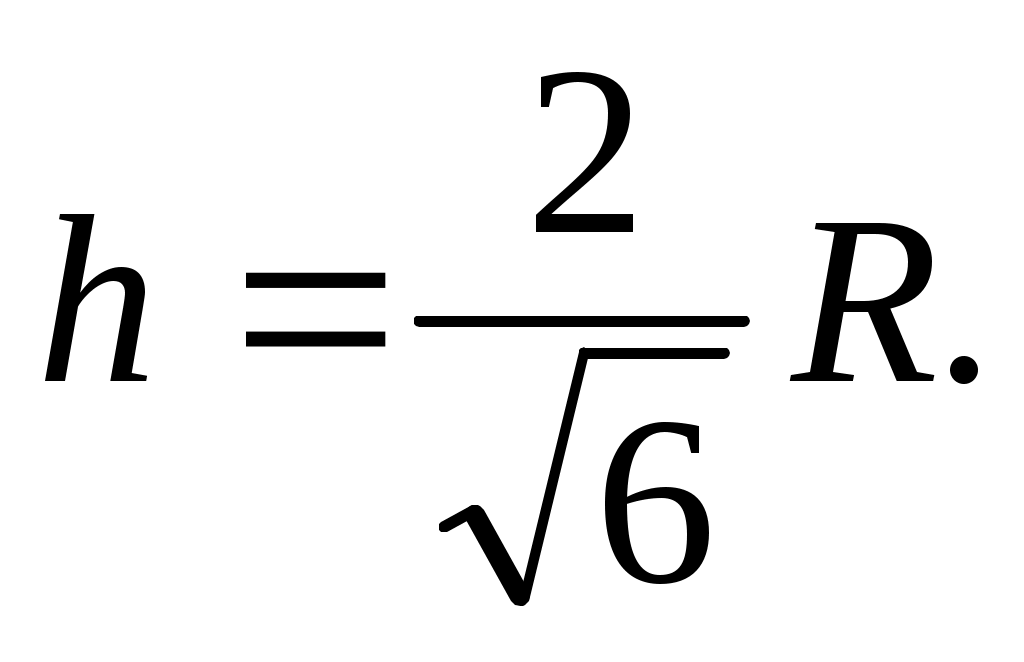
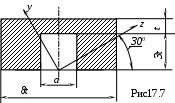
Пример 2.
Установить, при каком значении aоси z,yбудут главными осями сечения (рис.17.7).
Р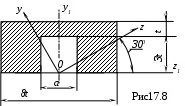 ешение.
ешение.
Вариант 1.
Проведем через точку О оси z1 , y1 . Эти оси будут главными, так как y1 – ось симметрии (рис. 17.8). Если
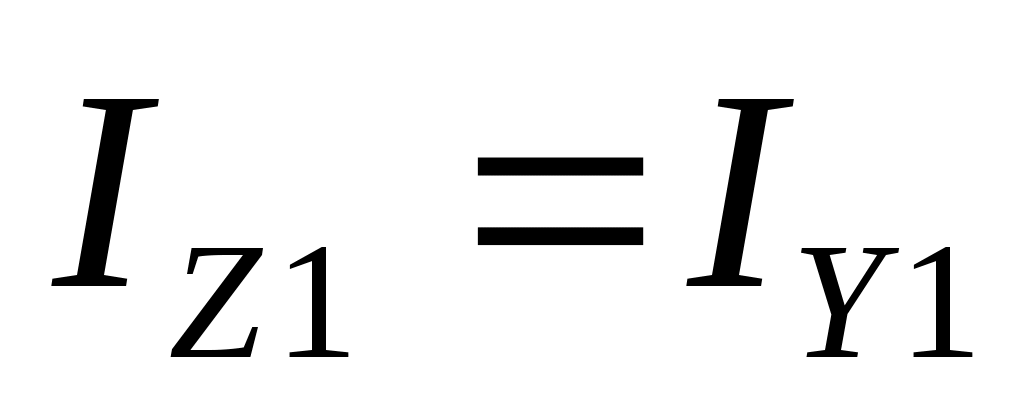 , то все оси (в том числе и оси z , y), проходящие через точку О, будут главными.
, то все оси (в том числе и оси z , y), проходящие через точку О, будут главными.
Найдем моменты инерции относительно осей z1 и y1, используя метод отрицательных площадей:
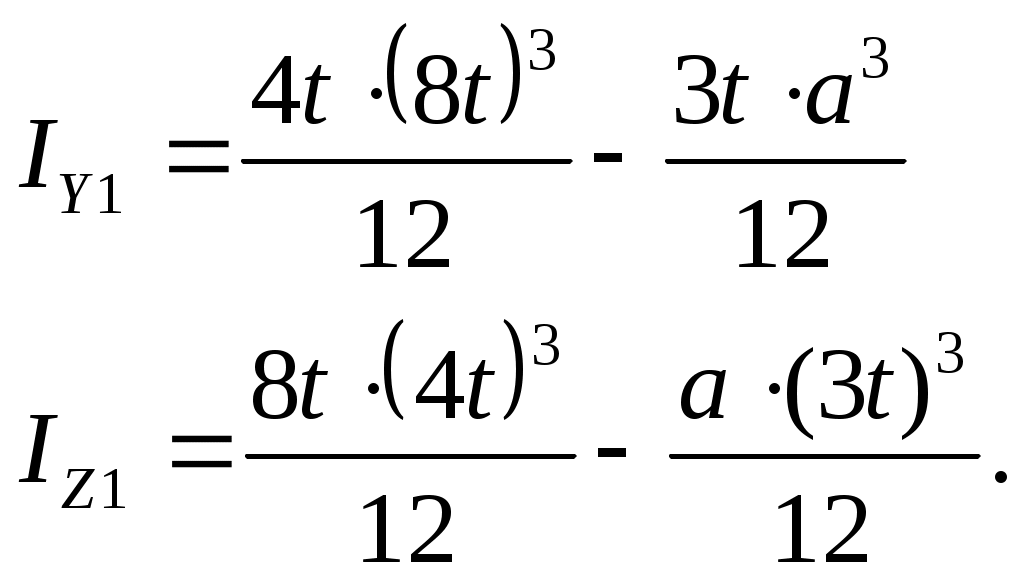
Откуда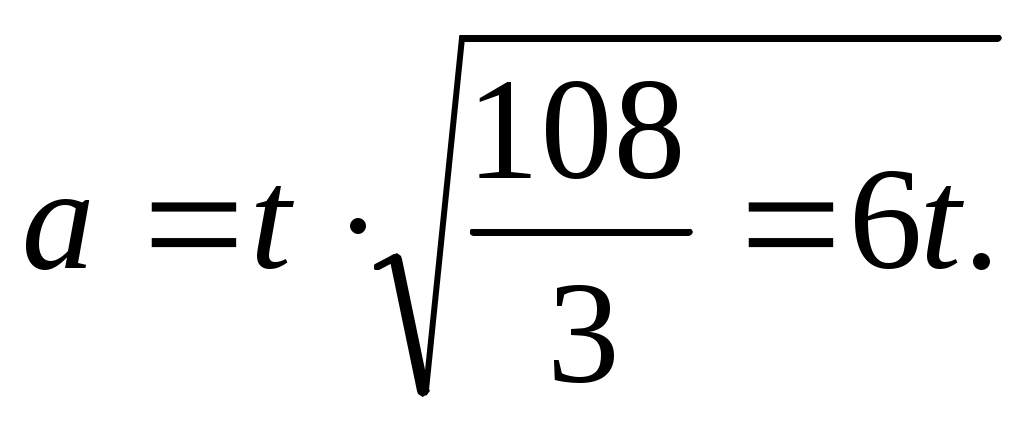
Вариант 2. По формуле (17.13), с учетом, что оси z , y должны быть главными,
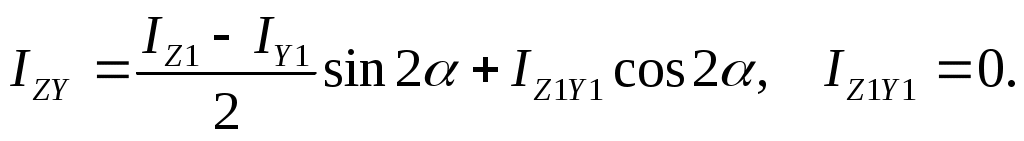
Так как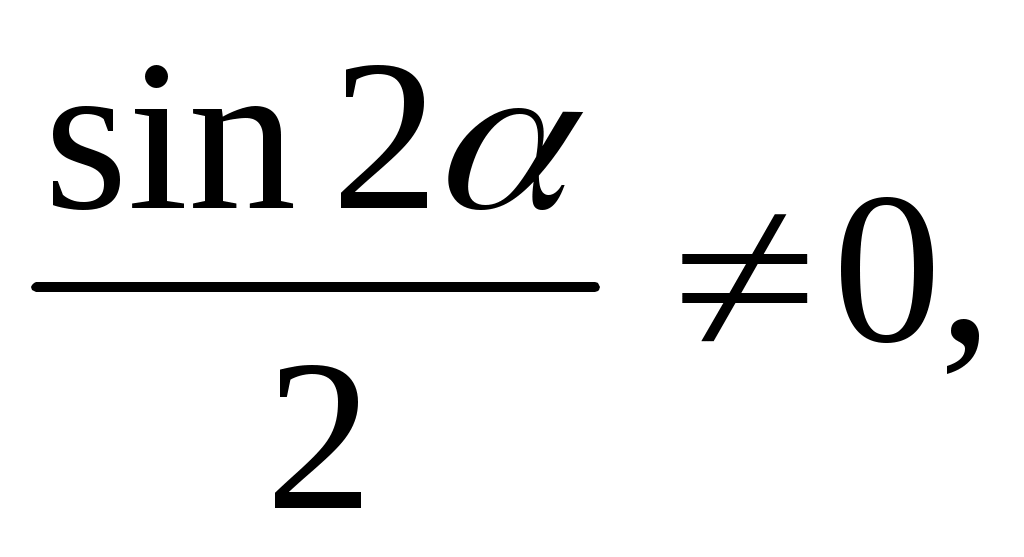 то, следовательно,
то, следовательно, 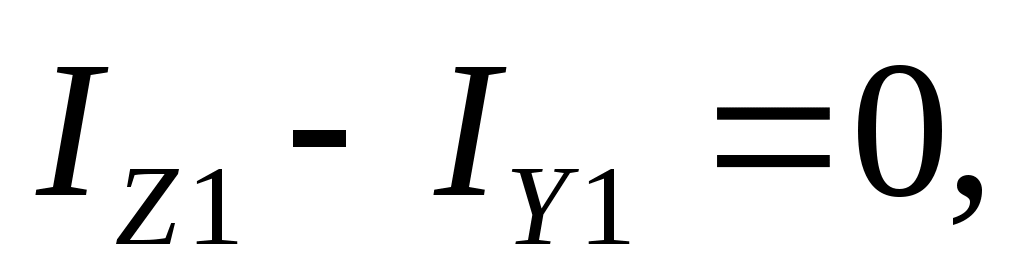 т.е. приходим к решению варианта 1.
т.е. приходим к решению варианта 1.
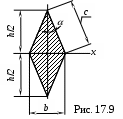
Пример 3. Балка, имеющая в поперечном сечении форму ромба, работает на изгиб в вертикальной плоскости. При каких отношенияхh/bпрогибы в балке будут наименьшие; нормальные напряжения будут наименьшие (Рис. 17.9).
Р Е Ш Е Н И Е

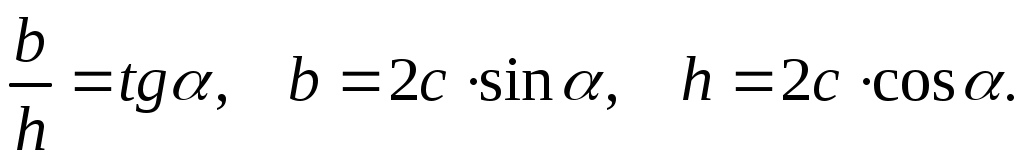
Тогда:
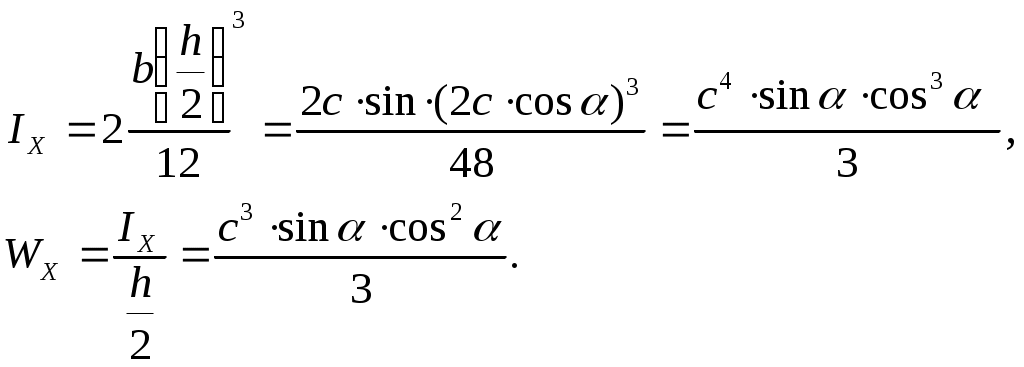
Так как прогибы обратно пропорциональны Ix, а нормальные напряжения обратно пропорциональны Wx, то исследуем Ix и Wx на экстремум:
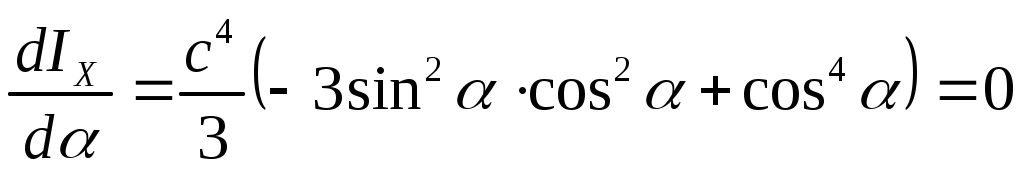
откуда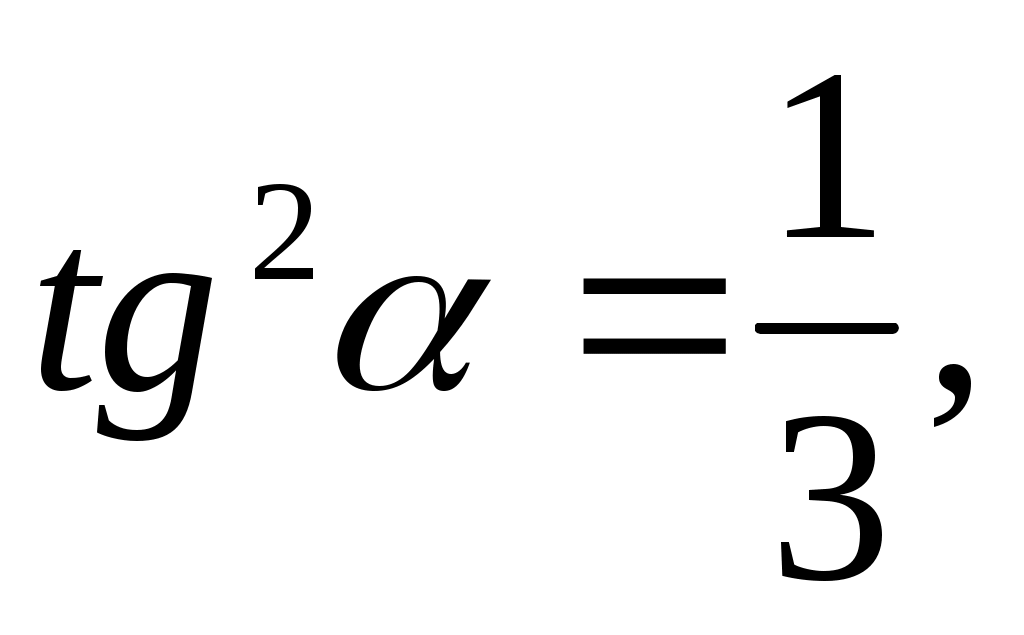 т.е. прогибы будут наименьшими при
т.е. прогибы будут наименьшими при 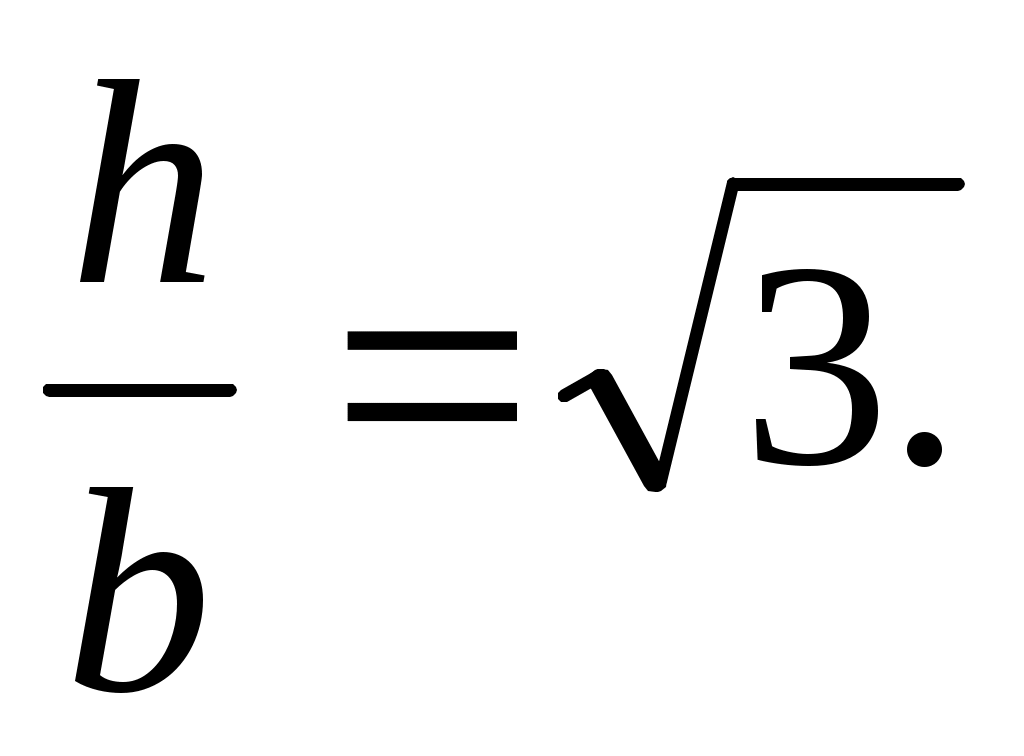
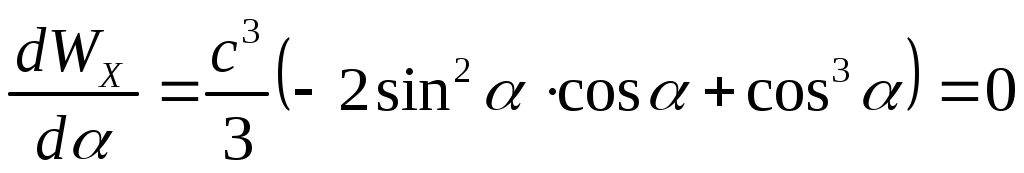
откуда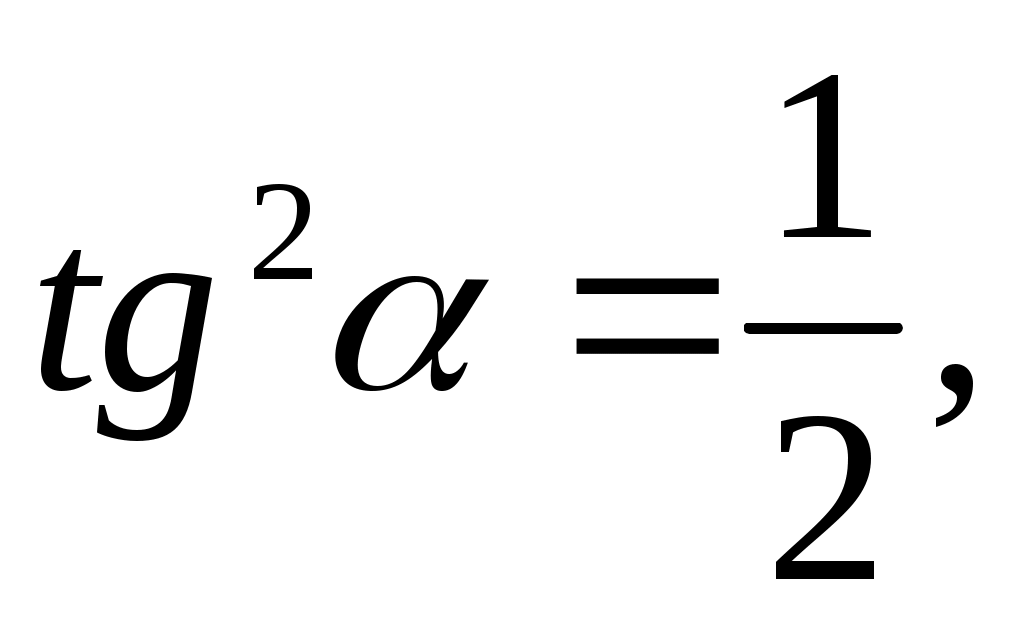 т.е. нормальные напряжения будут наименьшими при
т.е. нормальные напряжения будут наименьшими при 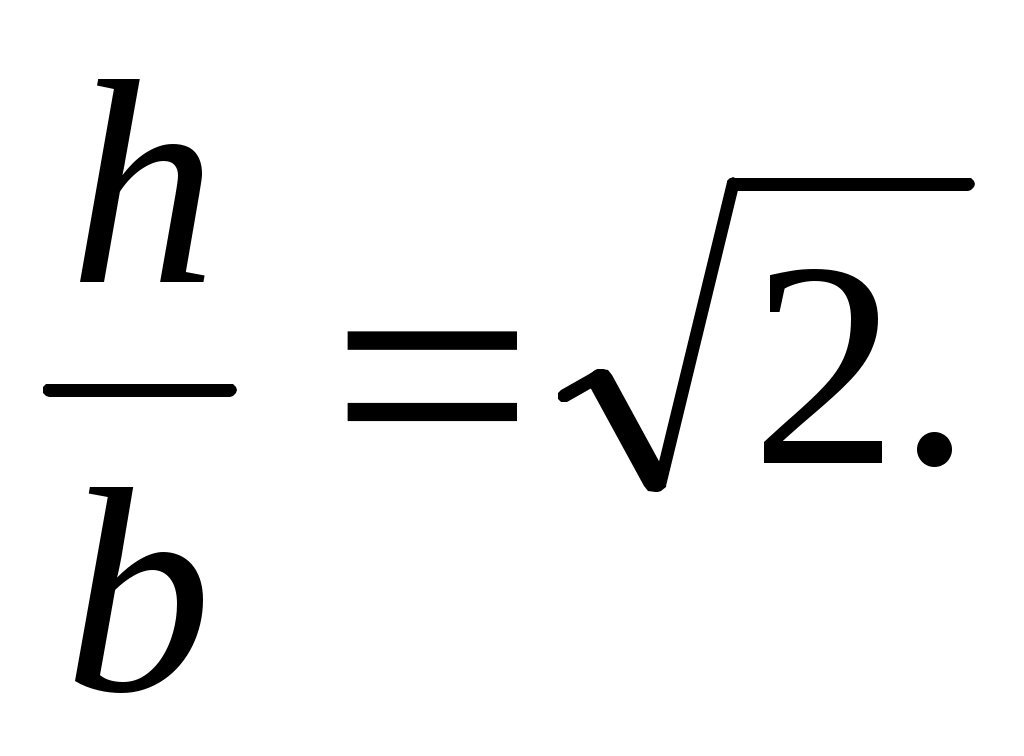
17.3. Геометрические характеристики простейших плоских сечений
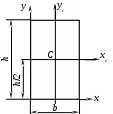
1. Прямоугольник
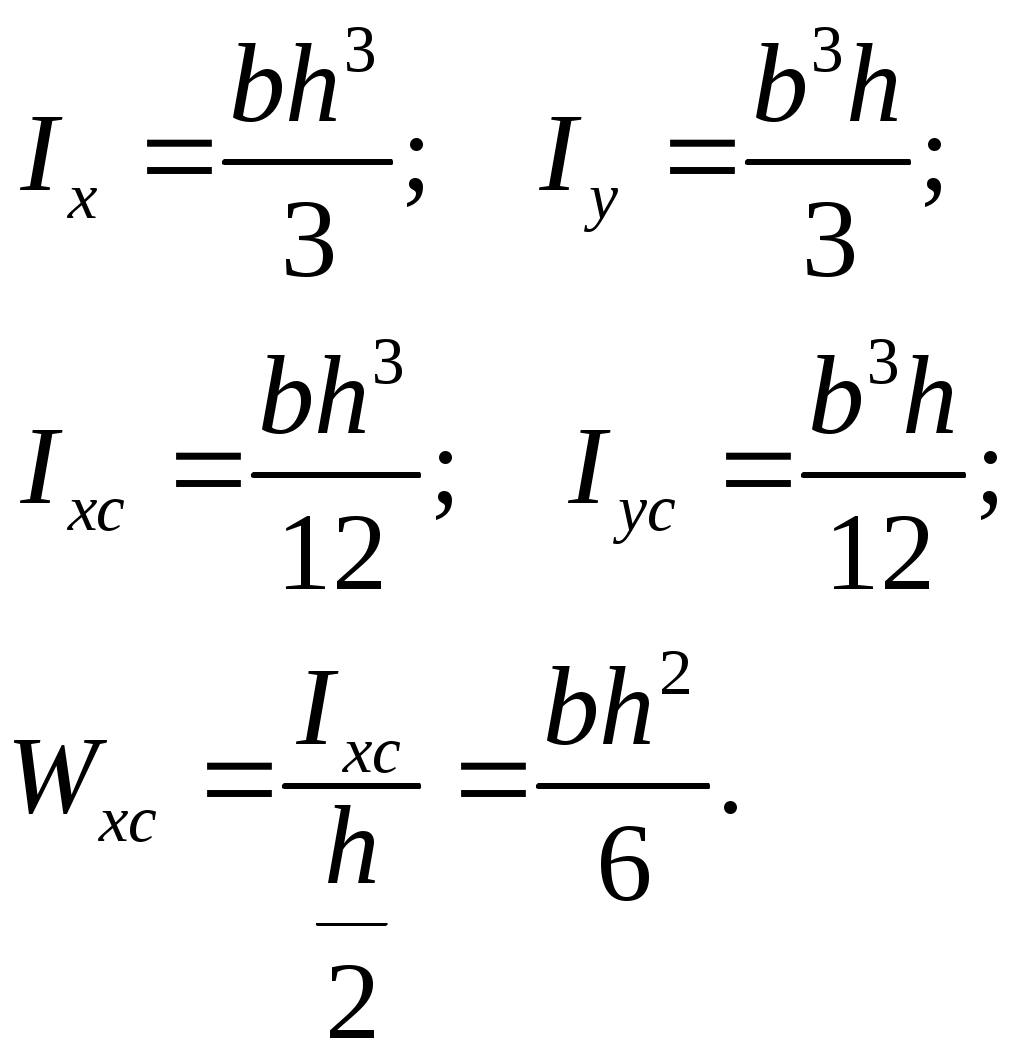
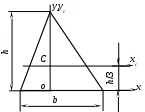
2. Треугольник
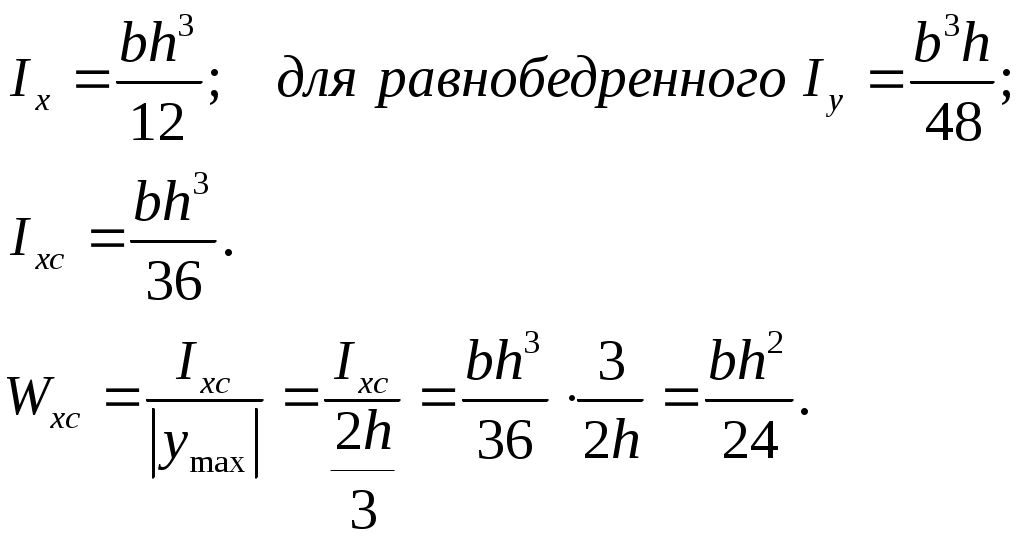
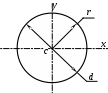
3. Круг
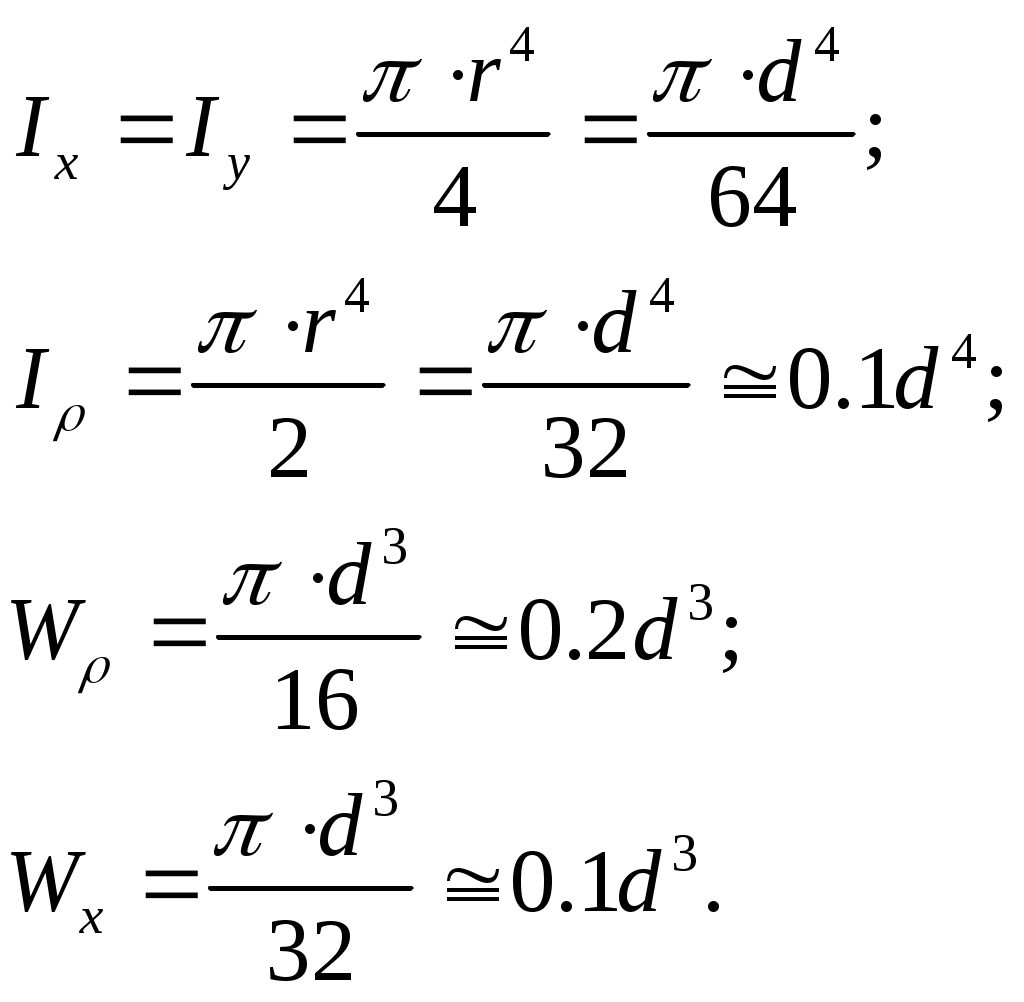
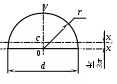
4. Полукруг
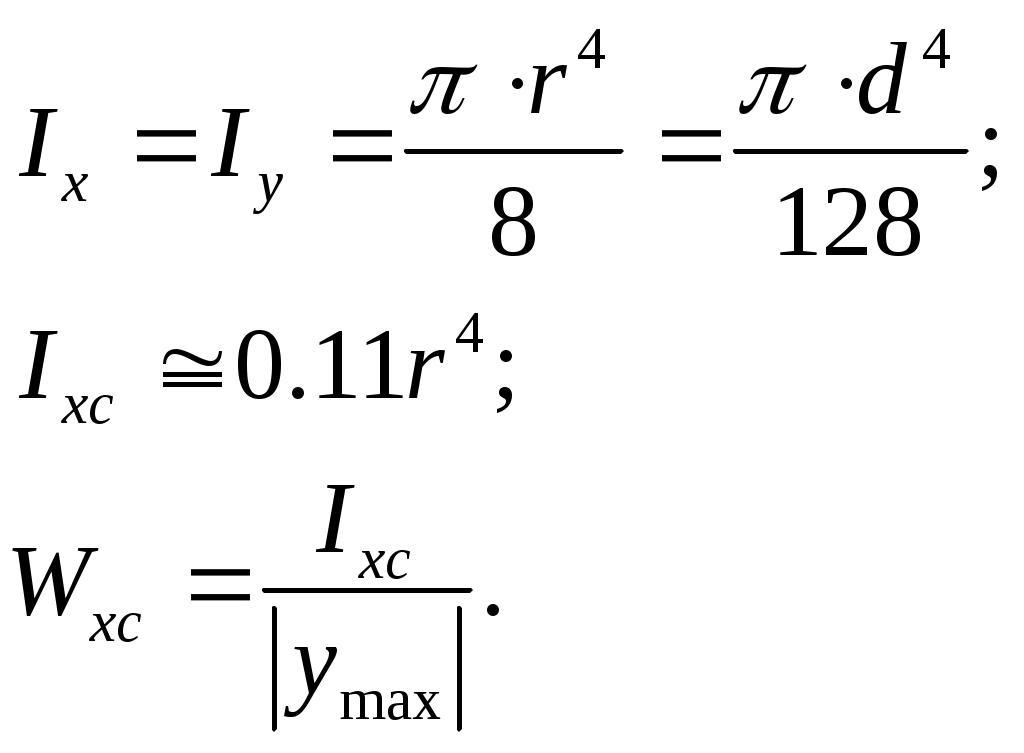
Вопросы для самопроверки
С П И С О К Л И Т Е Р А Т У Р Ы
Основная литература
1. Феодосьев В.Н. Сопротивление материалов: Учебник для вузов.- М.:изд-во МГТУ, 2003.-512с.
2. Сборник задач по сопротивлению материалов: Учебное пособие/ Под ред. Л.К. Паршина.-СПб.: Изд-во”Иван Федоров”,2003.- 432с.
3. Сборник задач по курсу «Сопротивление материалов»/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2005.-159с.
4. Прикладная механика. Раздел «Сопротивление материалов».Ч.1: Учебное пособие/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2000.-117с.:ил.
5. Прикладная механика. Раздел «Сопротивление материалов».Ч.11: Учебное пособие/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2001.-118с.:ил.
6. Прикладная механика. Раздел «Сопротивление материалов».Ч.111: Учебное пособие/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2002.-119с.:ил.
7. Попёнов А.И. Статически неопределимые задачи: Учебное пособие по сопротивлению материалов.- Уфа: Изд-во УГНТУ.-2010.-36с.:ил.
8. Лабораторные работы по курсу« Сопротивление материалов»./УГНТУ. Каф. Сопромата.- Уфа: Изд-во УГНТУ.-2003.-63с.:ил.
Дополнительная литература
1. Степин П.А. Сопротивление материалов: Учеб. для немашностр.спец.вузов.-М.: Высш. шк., 1988.-367с.:ил. и посл. изд-я.
2. Ицкович Г.М. и др. Руководство к решению задач по сопротивлению материалов. Учебное пособие для вузов.- М.Высш. школа,2001.-592с.
3. Миролюбов И.Н. и др. Пособие к решению задач по сопротивлению материалов. Учебное пособие для вузов.- .- СПб.: Изд-во «Лань», 2004.-399 с.
С О Д Е Р Ж А Н И Е
1.1. Задачи, цель и предмет курса……………………………………..…3
1.2. Реальные твердые тела и идеализированное тело
сопротивления материалов………………………… ……………..3
Вопросы для самопроверки…………………………………………..10
2. Эпюры внутренних силовых факторов…...……………………… 11
2.1. Правило знаков при построении эпюр…………………..…………..11
2.2. Дифференциальные зависимости между M,Qи q………………….12
2.3. Построение эпюр……………………………………………………..13
Вопросы для самопроверки…………………………………………..18
3. Растяжение и сжатие……………………………………………….....19
3.1.1 Напряжения в поперечных сечениях бруса…………………………19
3.1.2. Понятие о трёх основных задачах сопротивления мате-
риалов при центральном растяжении (сжатии) прямого бруса . ..20
3.1.3 Напряжения в наклонных сечениях бруса………………………….21
3.1.4. Закон парности касательных напряжений…………………………..23
3.2.1. Продольные деформаций. Закон Гука………………………………23
3.2.2. Поперечная деформация…………………………………..…………25
3.3. Деформация и напряжения при действии собственного веса……..26
3.4. Потенциальная энергия при растяжении и сжатии…………………27
3.5. Испытание материалов……………………………………………….29 3.5.1. Испытание материалов на растяжение………………………………29
3.5.1.1. Диаграмма растяжения………………………...………………...…29
3.5.1.2. Механические характеристики материалов……………………….29
3.5.1.3. Характеристики пластичности материалов……………………….33
3.5.1.4. Повышение предела пропорциональности при повторном
нагружении (наклёп)…………………………………………...….34
3.5.1.5. Сравнение диаграмм растяжения для различных материалов……………………………………………………….…35
3.5.2. Испытание материалов на сжатие…………….…..…………..…..36
3.5.2.1. Диаграмма сжатия, особенности разрушения при сжатии.............36
3.5.2.2. Эффект Баушингера……………………………...…………………39
3.6. Расчет по допускаемым напряжениям и перемещениям………..…40
3.6.1. Условие прочности и три основные задачи сопротивления материалов………………………………………………………...…..40
3.6.2. Условие жесткости и три основные задачи сопротивления материалов………………………………………………………..…..41
Вопросы для самопроверки…………………………………….……41
4.6.1. Задачи теории прочности ……………………………………………57
4.6.2. Первая теория прочности ………………………………………...…58
4.6.3. Вторая теория прочности…………………………………………….58
4.6.4. Третья теория прочности ……………………………………………58
4.6.5. Четвертая теория прочности ………………………………………..60
К геометрическим характеристикам плоских сечений относятся также неинтегральные характеристики:
радиус инерции сечения относительно центральных осей
осевые моменты сопротивления сечения относительно главных центральных осей
где ymax – ордината наиболее удаленных от оси Z точек сечения (рис.17.4,а,б);
полярный момент сопротивления круглого сечения
где max=r– расстояние до наиболее удаленной точки от центра круглого сечения.
Учитывая свойство аддитивности геометрических характеристик, во многих задачах при их решении удобно достроить заданное сечение до такой простой фигуры, для которой геометрические характеристики известны.


Пример 1. Определить величину размера h для фигуры (рис.17.5), при котором центр тяжести её будет находиться на прямой АВ
(R –задан).
Решение
 Для того чтобы центр тяжести находился на прямой АВ, последняя должна совпадать с центральной осью ZC. Следовательно статический момент всей площади фигуры
Для того чтобы центр тяжести находился на прямой АВ, последняя должна совпадать с центральной осью ZC. Следовательно статический момент всей площади фигуры 
Пример 2.
Установить, при каком значении aоси z,yбудут главными осями сечения (рис.17.7).
Р
 ешение.
ешение. Вариант 1.
Проведем через точку О оси z1 , y1 . Эти оси будут главными, так как y1 – ось симметрии (рис. 17.8). Если
Найдем моменты инерции относительно осей z1 и y1, используя метод отрицательных площадей:
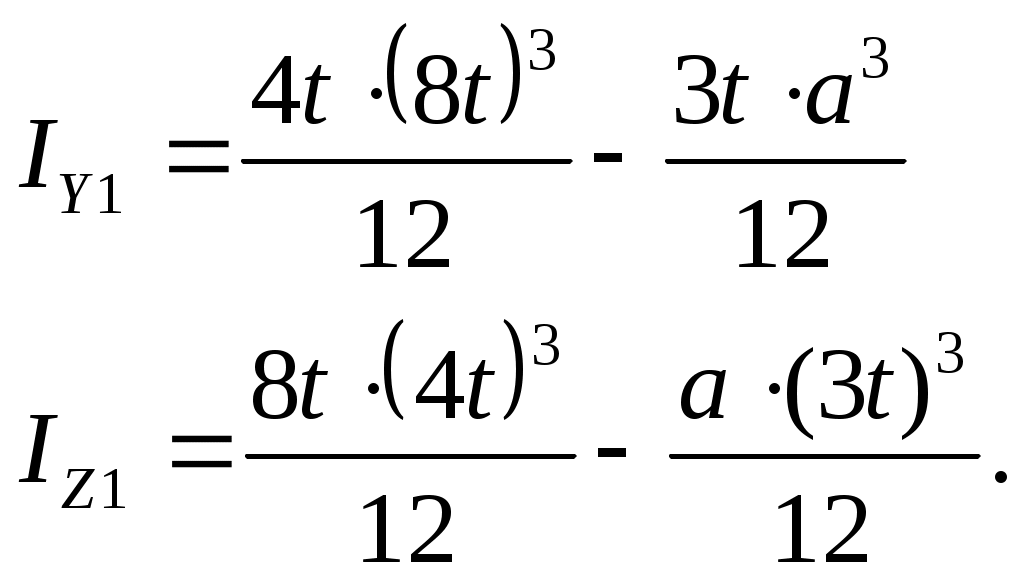
Откуда
Вариант 2. По формуле (17.13), с учетом, что оси z , y должны быть главными,
Так как

Пример 3. Балка, имеющая в поперечном сечении форму ромба, работает на изгиб в вертикальной плоскости. При каких отношенияхh/bпрогибы в балке будут наименьшие; нормальные напряжения будут наименьшие (Рис. 17.9).
Р Е Ш Е Н И Е
Тогда:
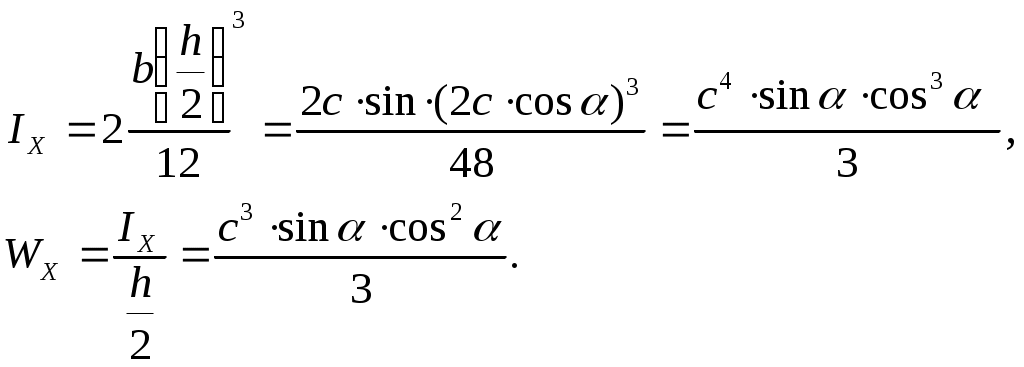
Так как прогибы обратно пропорциональны Ix, а нормальные напряжения обратно пропорциональны Wx, то исследуем Ix и Wx на экстремум:
откуда
откуда
17.3. Геометрические характеристики простейших плоских сечений
1. Прямоугольник

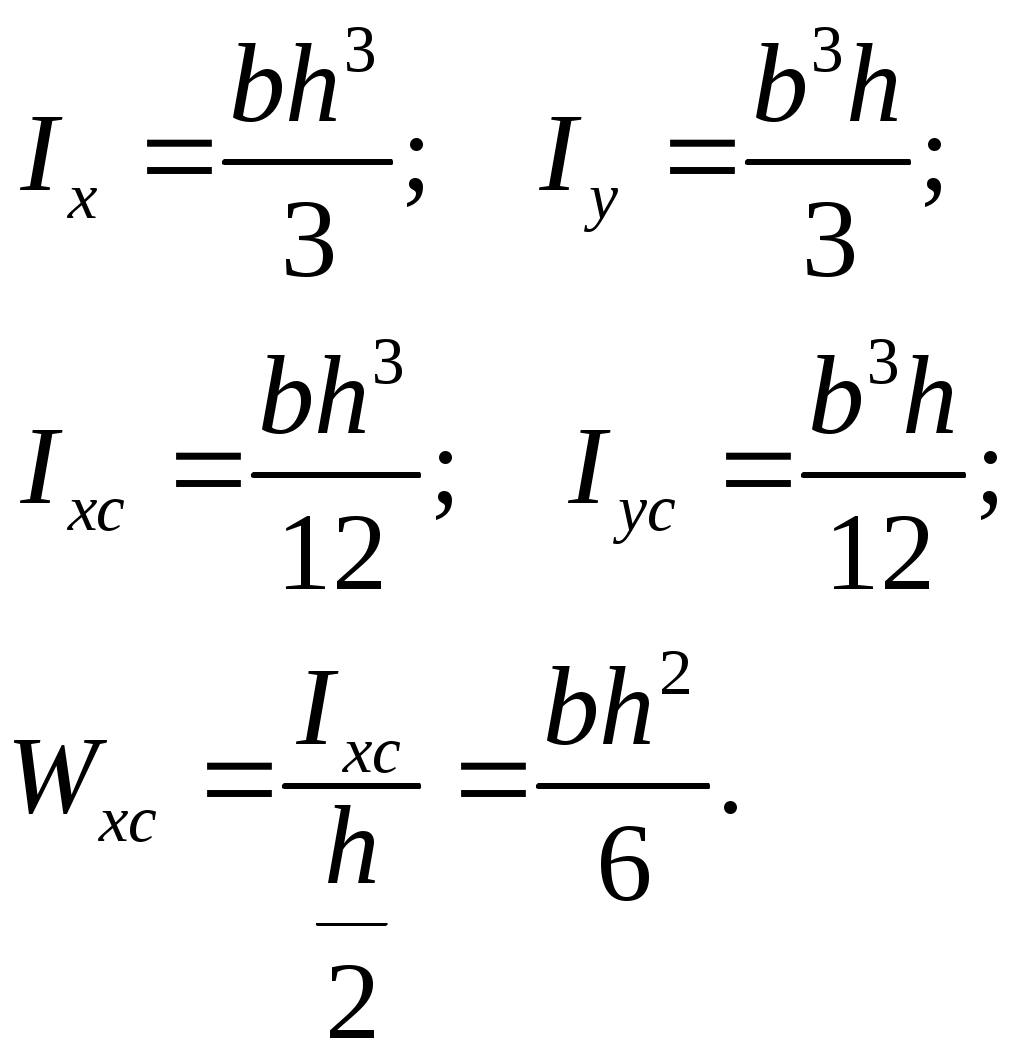
2. Треугольник

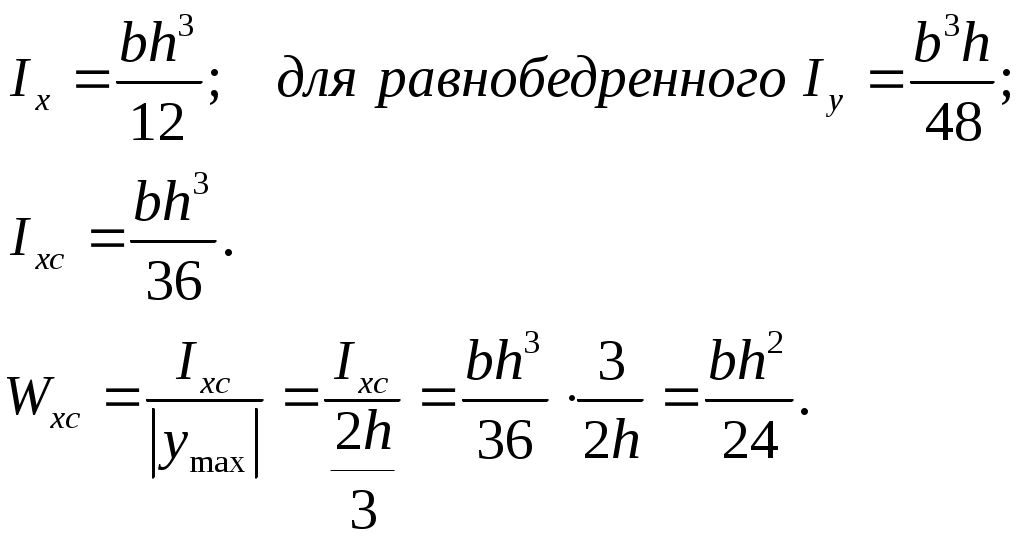
3. Круг
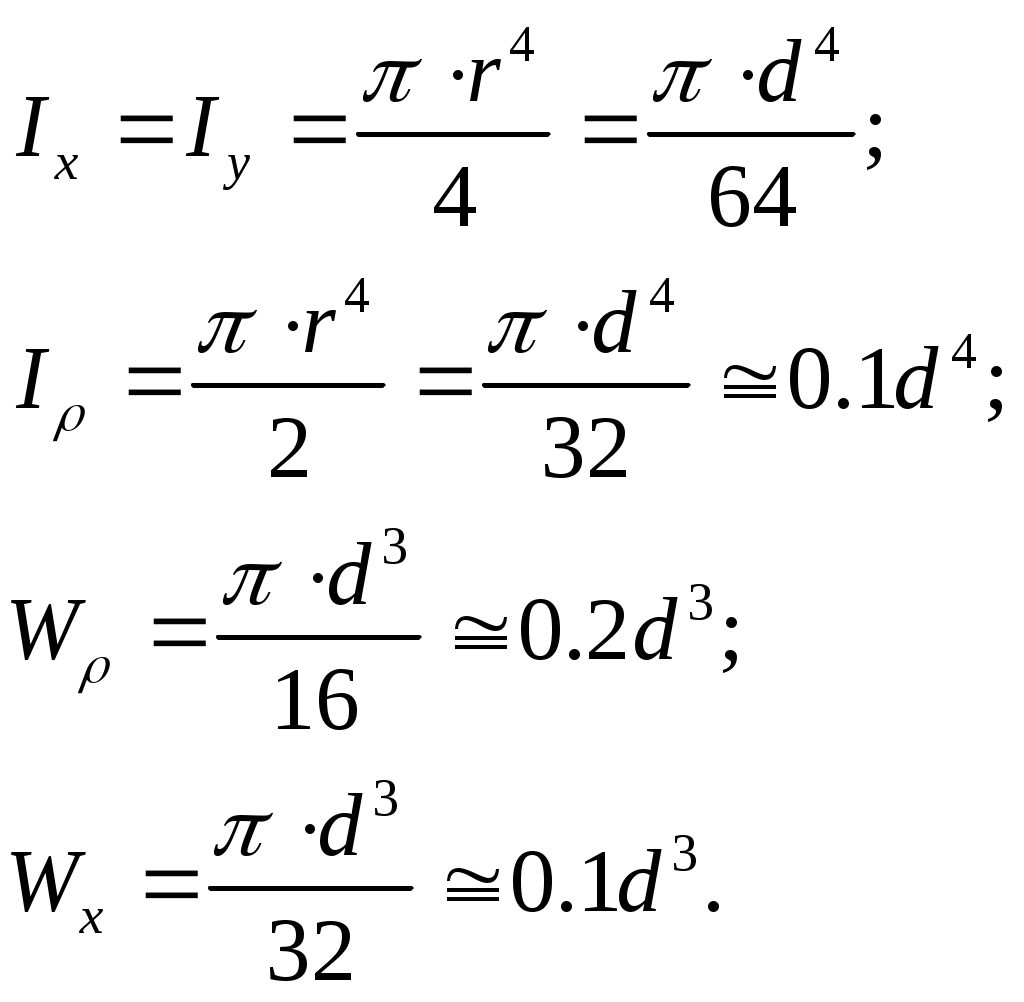

4. Полукруг

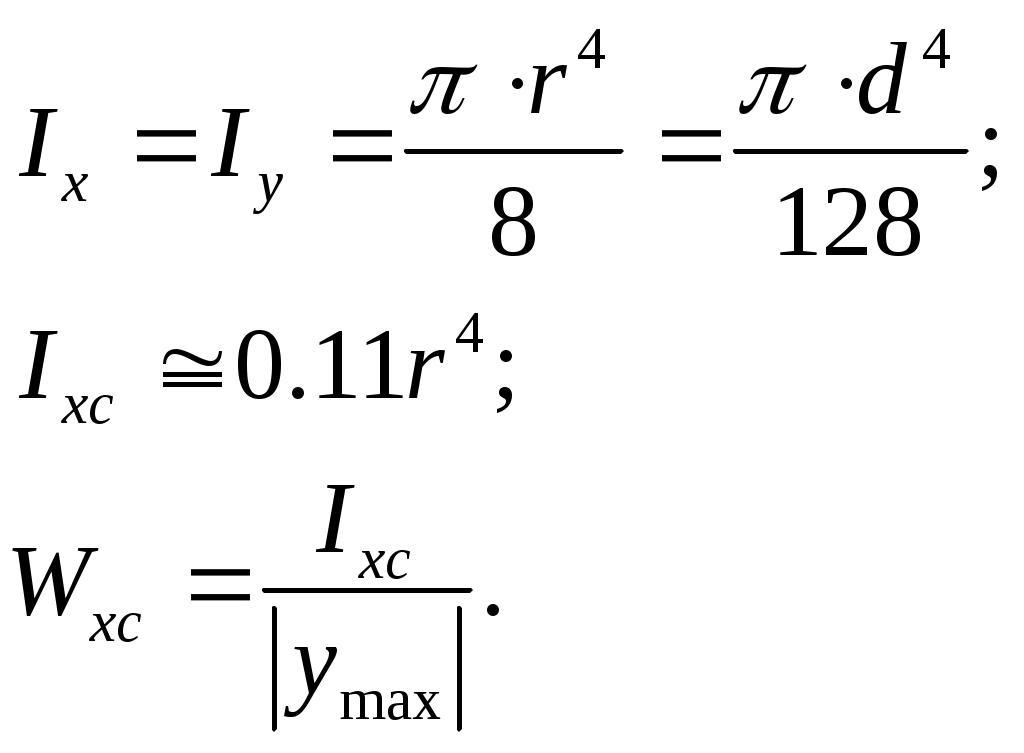
Вопросы для самопроверки
-
Какие геометрические характеристики сечения называются моментами инерции? -
Может ли статический момент быть отрицательным? -
Какова размерность статический момента? -
Какая существует связь между полярным и осевыми моментами инерции? -
В каком случае можно сразу заметить, что центробежный момент сечения равен нулю? -
Какие оси и моменты инерции называются главными? -
Какая зависимость между моментами инерции относительно парал- лельных осей, одна из которых центральная? -
Какая зависимость между моментами инерции для двух систем координат с общим началом ординат, повернутых относительно друг друга на угол ?
С П И С О К Л И Т Е Р А Т У Р Ы
Основная литература
1. Феодосьев В.Н. Сопротивление материалов: Учебник для вузов.- М.:изд-во МГТУ, 2003.-512с.
2. Сборник задач по сопротивлению материалов: Учебное пособие/ Под ред. Л.К. Паршина.-СПб.: Изд-во”Иван Федоров”,2003.- 432с.
3. Сборник задач по курсу «Сопротивление материалов»/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2005.-159с.
4. Прикладная механика. Раздел «Сопротивление материалов».Ч.1: Учебное пособие/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2000.-117с.:ил.
5. Прикладная механика. Раздел «Сопротивление материалов».Ч.11: Учебное пособие/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2001.-118с.:ил.
6. Прикладная механика. Раздел «Сопротивление материалов».Ч.111: Учебное пособие/ Быков Л.И. и др.-Уфа: Изд-во УГНТУ.-2002.-119с.:ил.
7. Попёнов А.И. Статически неопределимые задачи: Учебное пособие по сопротивлению материалов.- Уфа: Изд-во УГНТУ.-2010.-36с.:ил.
8. Лабораторные работы по курсу« Сопротивление материалов»./УГНТУ. Каф. Сопромата.- Уфа: Изд-во УГНТУ.-2003.-63с.:ил.
Дополнительная литература
1. Степин П.А. Сопротивление материалов: Учеб. для немашностр.спец.вузов.-М.: Высш. шк., 1988.-367с.:ил. и посл. изд-я.
2. Ицкович Г.М. и др. Руководство к решению задач по сопротивлению материалов. Учебное пособие для вузов.- М.Высш. школа,2001.-592с.
3. Миролюбов И.Н. и др. Пособие к решению задач по сопротивлению материалов. Учебное пособие для вузов.- .- СПб.: Изд-во «Лань», 2004.-399 с.
С О Д Е Р Ж А Н И Е
-
Введение……………………………………………………………….3
1.1. Задачи, цель и предмет курса……………………………………..…3
1.2. Реальные твердые тела и идеализированное тело
сопротивления материалов………………………… ……………..3
-
1.3. Реальная конструкция и её расчетная схема………............................5 -
1.4. Внешние силы……………………………………………………… ..5 -
1.5. Внутренние силы в стержне и их определение………………………6 -
1.6. Понятие о напряжениях в точке………………………………………7 -
1.7. Связь между напряжениями внутренними силами………………….8 -
1.8. Понятие о деформациях в точке………………………………………9
Вопросы для самопроверки…………………………………………..10
2. Эпюры внутренних силовых факторов…...……………………… 11
2.1. Правило знаков при построении эпюр…………………..…………..11
2.2. Дифференциальные зависимости между M,Qи q………………….12
2.3. Построение эпюр……………………………………………………..13
Вопросы для самопроверки…………………………………………..18
3. Растяжение и сжатие……………………………………………….....19
3.1.1 Напряжения в поперечных сечениях бруса…………………………19
3.1.2. Понятие о трёх основных задачах сопротивления мате-
риалов при центральном растяжении (сжатии) прямого бруса . ..20
3.1.3 Напряжения в наклонных сечениях бруса………………………….21
3.1.4. Закон парности касательных напряжений…………………………..23
3.2.1. Продольные деформаций. Закон Гука………………………………23
3.2.2. Поперечная деформация…………………………………..…………25
3.3. Деформация и напряжения при действии собственного веса……..26
3.4. Потенциальная энергия при растяжении и сжатии…………………27
3.5. Испытание материалов……………………………………………….29 3.5.1. Испытание материалов на растяжение………………………………29
3.5.1.1. Диаграмма растяжения………………………...………………...…29
3.5.1.2. Механические характеристики материалов……………………….29
3.5.1.3. Характеристики пластичности материалов……………………….33
3.5.1.4. Повышение предела пропорциональности при повторном
нагружении (наклёп)…………………………………………...….34
3.5.1.5. Сравнение диаграмм растяжения для различных материалов……………………………………………………….…35
3.5.2. Испытание материалов на сжатие…………….…..…………..…..36
3.5.2.1. Диаграмма сжатия, особенности разрушения при сжатии.............36
3.5.2.2. Эффект Баушингера……………………………...…………………39
3.6. Расчет по допускаемым напряжениям и перемещениям………..…40
3.6.1. Условие прочности и три основные задачи сопротивления материалов………………………………………………………...…..40
3.6.2. Условие жесткости и три основные задачи сопротивления материалов………………………………………………………..…..41
Вопросы для самопроверки…………………………………….……41
-
Напряженное и деформированное состояние в точке………..…….43
-
Понятие напряженного состояния в точке и его виды……………43 -
Напряжения в наклонных площадках при плоском напряженном состоянии………………………………………………………….…44 -
Главные напряжения…………………………………………...…....46 -
Экстремальные касательные напряжения……………………….…48 -
Круг Мора……………………………………………………………49
-
Деформированное состояние в точке…………..………………..…52-
Главные деформации. Удлинение в произвольном направлении………………………..…………………………………................52 -
Аналогия между зависимостями для напряженного и деформированного состояний в точке………………………..…………..……...54
-
-
Обобщенный закон Гука для линей упругого тела…….........….…55 -
Относительная объёмная деформация……………………………56 -
Потенциальная энергия при объёмном напряжённом состоянии....56 Вопросы для самопроверки…………………………………………57 -
Теории прочности ……………………………………………………57
4.6.1. Задачи теории прочности ……………………………………………57
4.6.2. Первая теория прочности ………………………………………...…58
4.6.3. Вторая теория прочности…………………………………………….58
4.6.4. Третья теория прочности ……………………………………………58
4.6.5. Четвертая теория прочности ………………………………………..60