Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 381
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
. Этот коэффициент определяется как отношение предела выносливости при симметричных циклах образца сданной поверхностью к пределу выносливости образца с полированной поверхностью.
Абсолютные размеры детали.
Экспериментально установлено, что размеры детали существенно влияют на величину предела выносливости. С увеличением размеров предел выносливости уменьшается. Так, например, предел выносливости для стали, идущей на изготовление вагонных осей, определенный в лаборатории на образцах диаметром d=7,5 мм, равен 230 МПа. В действительности предел выносливости вагонной оси с диаметром d=170 мм, равен 120 МПа, что почти вдвое меньше лабораторных результатов.
До настоящего времени этому факту нет полного объяснения. Изменение величины предела выносливости в связи с изменением размеров образцов оценивается так называемым масштабным коэффициентом . Масштабным коэффициентом называют отношение предела выносливости детали к пределу выносливости образца диаметром 6 -12 мм.
Внешняя среда.
Усталостная прочность детали зависит от среды, в которой находится деталь. Коррозия среды ( вода, солёная вода, кислоты, пары) резко снижают усталостную прочность. Применение защитных покрытий поверхностей (окраска, металлизация, азотирование, цианирование, цементация, цинкование, плазменное напыление и др.) уменьшает эффект коррозионной среды.
Высокие температуры уменьшают, а низкие несколько повышают усталостную прочность, однако нужно иметь в виду, что при низких температурах резко снижается ударная вязкость.
16.6. Расчёт на прочность при переменных напряжениях
В расчётах на прочность при переменных напряжениях прочность детали принято оценивать по величине фактического коэффициента запаса n,сравнивая его с допускаемым коэффициента запаса [n], устанавливаемым нормами. Условие прочности записывается в виде
n [n].
Коэффициенты запаса n можно определить приближенно с помощью схематизированных диаграмм предельных амплитуд, например, показанной на рис. 16.9, б. Из начала координат проводим луч 01 под углом 1, который соответствует подобным циклам. Точка
М на котором с координатами а и mхарактеризует рабочий цикл. Точка N с координатами nа и nmхарактеризует предельное значение этого же цикла. Таким образом, фактического коэффициента запаса n можно определить как отношение отрезком
ON/OM.
Если луч 01 пересекает прямую АВ, рост напряжений цикла вызывает в образце усталостное разрушение. Коэффициент запаса по отношению к усталостному разрушению в этом случае обозначается nR и определяется из следующих соображений: Точка Nнаходится на прямой АВ и удовлетворяет уравнению (16.13), которое принимает вид
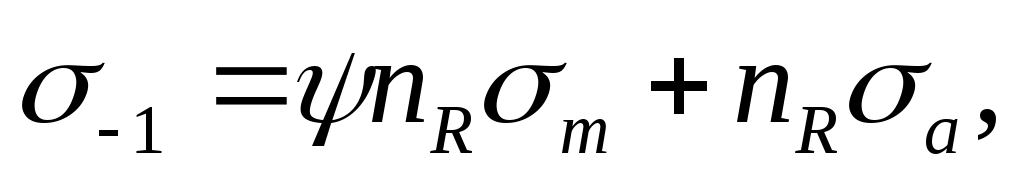 (16.15)
(16.15)
откуда
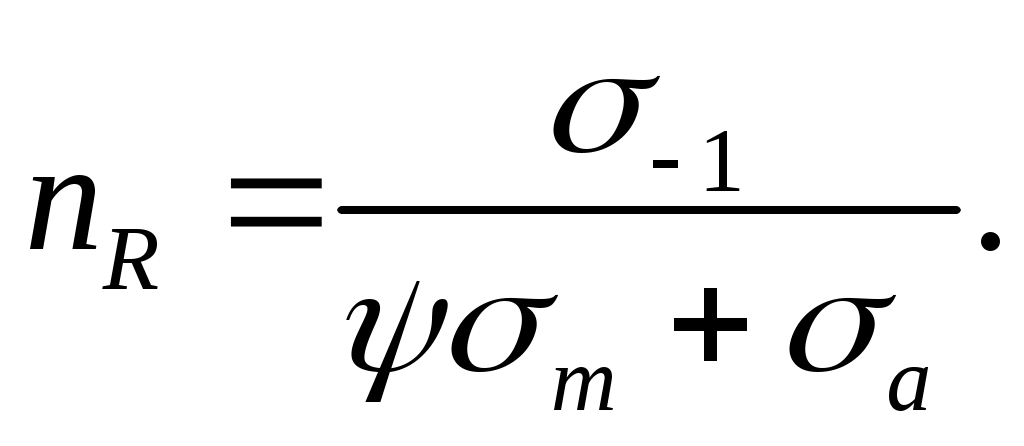 (16.16)
(16.16)
Получен коэффициент запаса для гладкого образца. Прочность детали зависит от размеров и формы этой детали, от состояния её поверхности. Всё это учитывается соответствующими коэффициентами, в нашем случае эффективным коэффициентом концентрации напряжений k , коэффициентом поверхностной чувствительности, масштабным коэффициентом. Тогда уравнение (16.15) примет вид

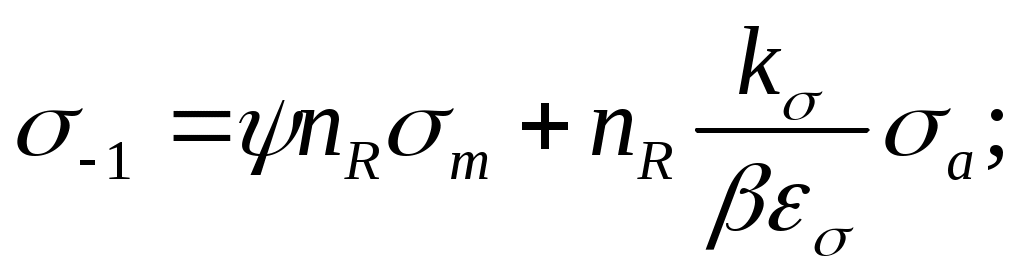 (16.17)
(16.17)
коэффициент запаса детали будет равен

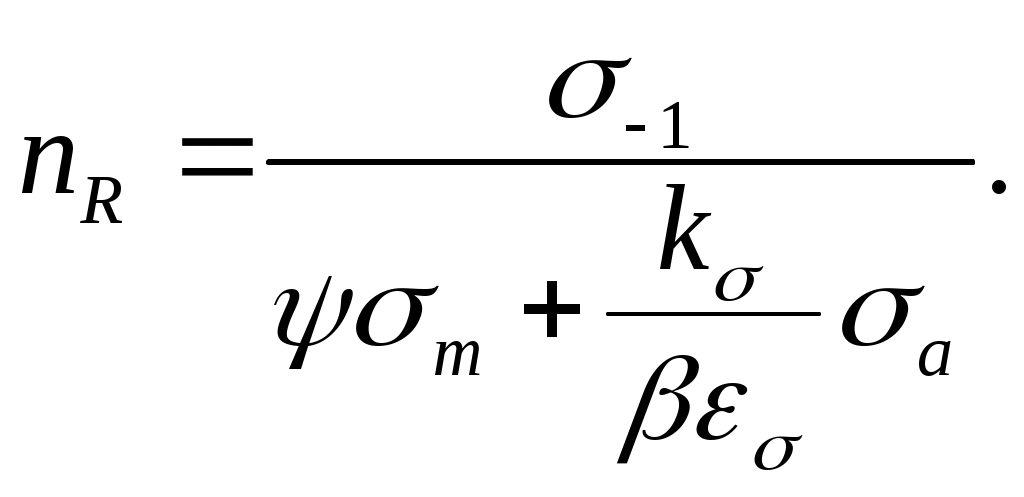 (16.18)
(16.18)
Вопросы для самопроверки
1. Что такое усталость материалов?
2. Что такое выносливость ?
3. Как объясняется возникновение трещины усталости в материале?
4. Что такое коэффициент асимметрии?
5. Что такое предел выносливости?
6. Все ли материалы имеют предел выносливости?
7. Какие коэффициенты учитываются при определении коэффициента запаса детали?
17. Геометрические характеристики плоских сечений
17.1. Введение
При решении задач о прочности и жесткости стержней, как было показано, такой характеристики поперечного сечения, как площадь
А, оказалось недостаточно. Так, например, при расчетах стержней на кручение понадобилось ввести понятие полярного момента инерции круглого сечения IPи момента сопротивления того же сечения при кручении WP. В дальнейшем понадобились ещё некоторые новые геометрические характеристики, для которых так же были получены формулы, позволяющие вычислять эти величины в простейших случаях. Однако в инженерной практике нередко приходится иметь дело с более сложными вариантами. В этих случаях сложное сечение представляют в виде фрагментов, вычисляют их геометрические характеристики, а затем по особым законам эти характеристики суммируют. Цель этой главы – ознакомить как с этими законами, так и с некоторыми инженерными рекомендациями, из них вытекающими.
К геометрическим характеристикам плоских сечений (рис. 17.1) относятся:
площадь сечения
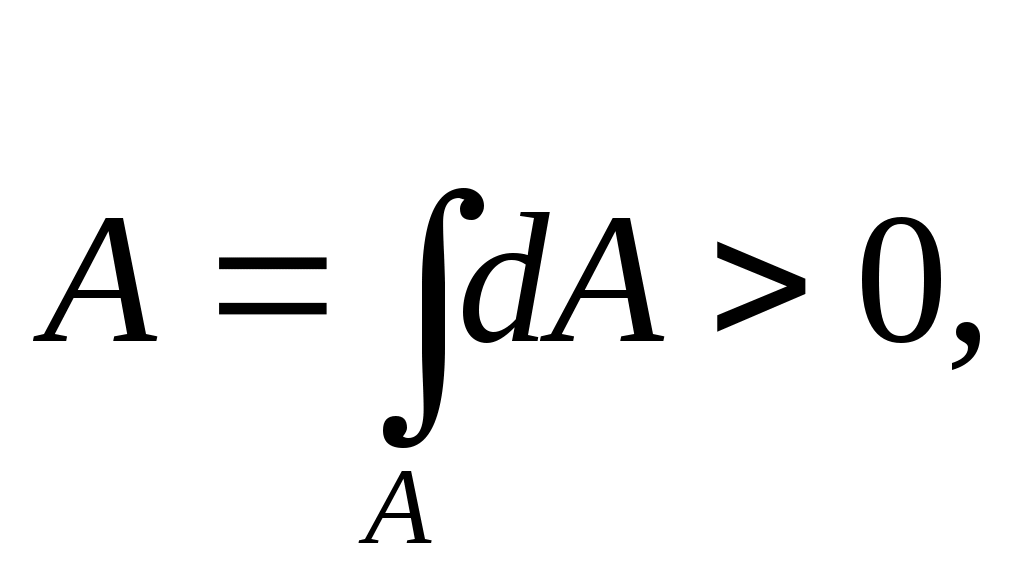 [м2]; (17.1)
[м2]; (17.1)
статический момент площади сечения относительно оси
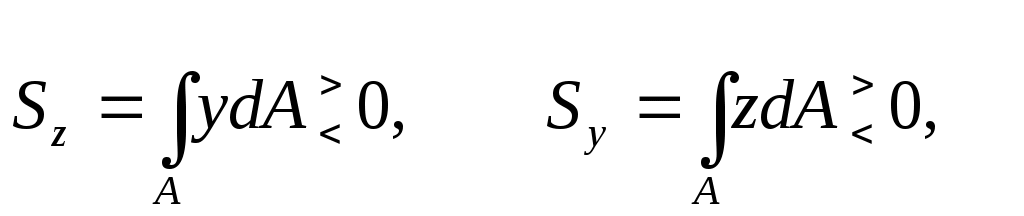 [м3]; (17.2)
[м3]; (17.2)
осевой момент инерции
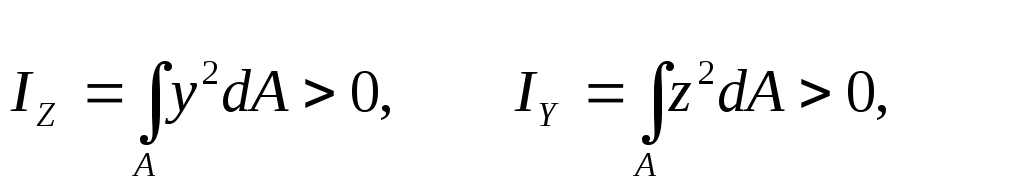 [м4]; (17.3)
[м4]; (17.3)
полярный момент инерции
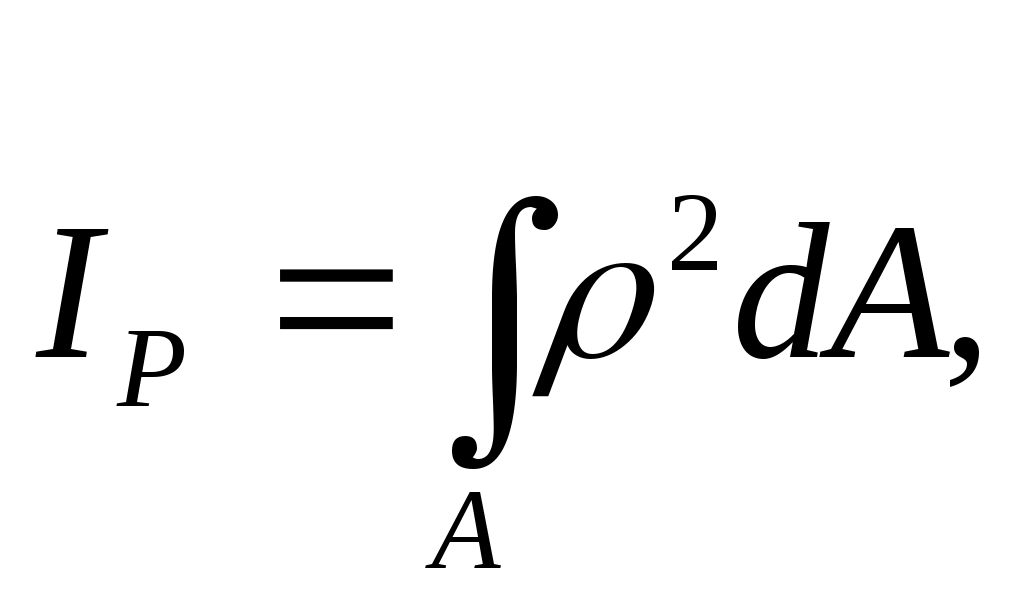 [м4]; (17.4)
[м4]; (17.4)
центробежный момент инерции
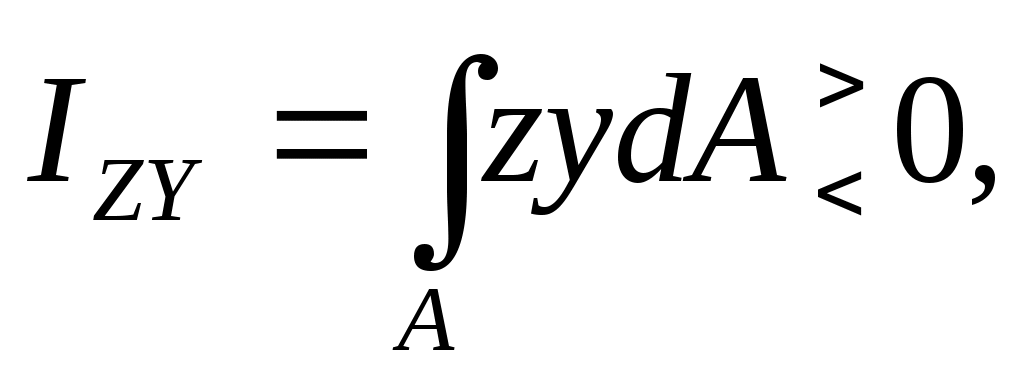 [м4]. (17.5)
[м4]. (17.5)
Все геометрические характеристики обладают свойством аддитивности.
При рассмотрении плоских сечений оперируют понятием центром масс бесконечно тонкой однородной пластинки постоянной толщины, имеющей то же очертание и размеры, что и данное сечение.
На основании теоремы о моменте равнодействующей
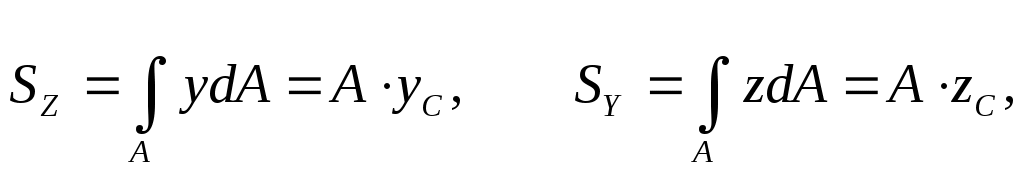 (17.6)
(17.6)
где А- площадь сечения; yc , zc– координаты центра тяжести сечения (ЦТ или С), откуда
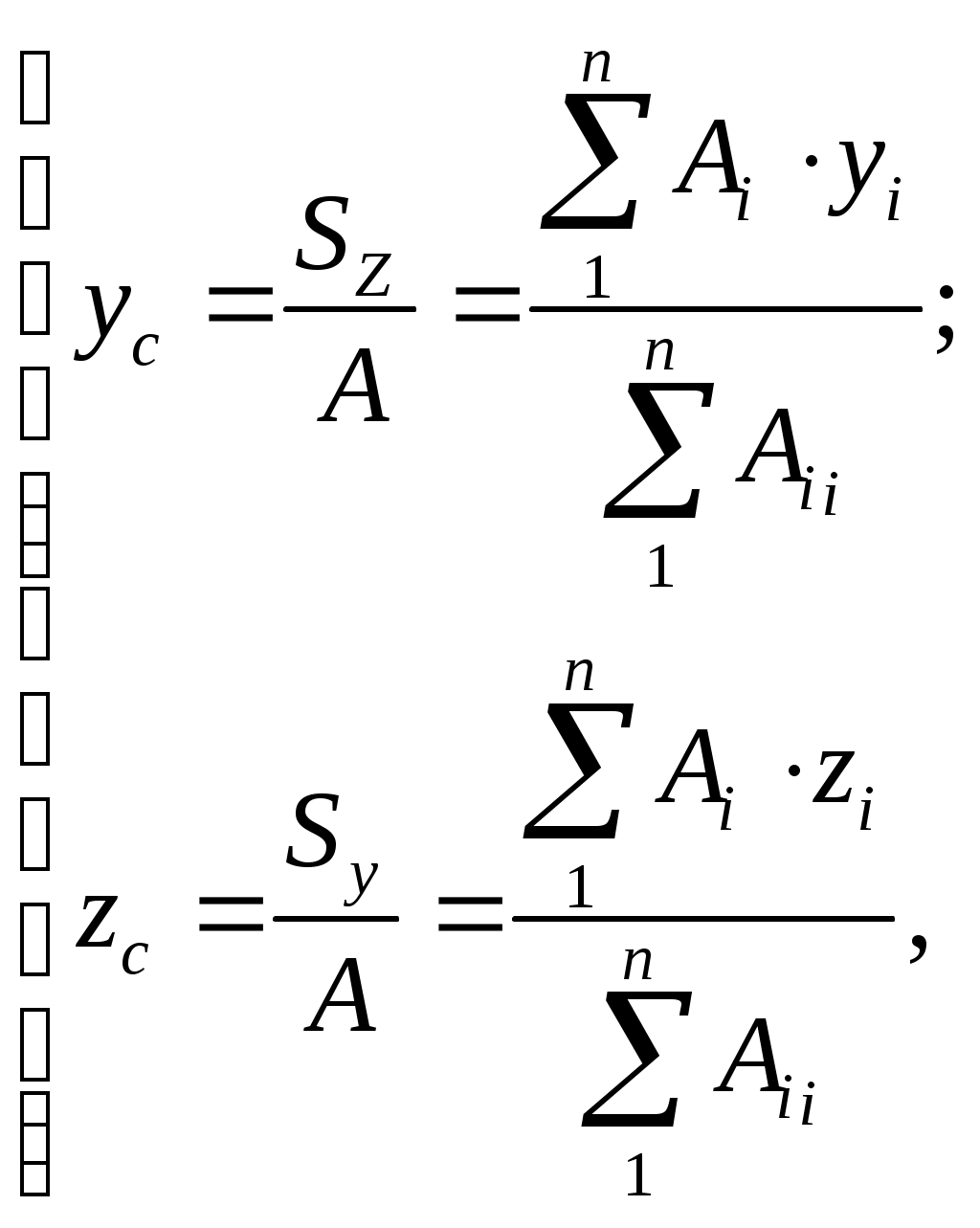 (17.7)
(17.7)
где Аi ,уi ,zi– соответственно площади, координаты центра тяжести простых сечений, составляющих данное сложное сечение.
Оси, проходящие через центр тяжести сечения,
называют центральными.
Из (17.6) следует, что если ось Z
с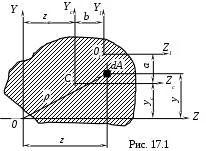 овпадает с центральной осью ZС , т.е. ус=0, то SZ= SZc=0,
овпадает с центральной осью ZС , т.е. ус=0, то SZ= SZc=0,
откуда выводы:
статический момент площади сечения относительно центральной оси равен нулю;
ось, относительно которой статический момент площади сечения равен нулю, является центральной;
оси симметрии всегда являются центральными.
Так как 2=z 2+y2, то, подставляя 2в (17.4), получим, что
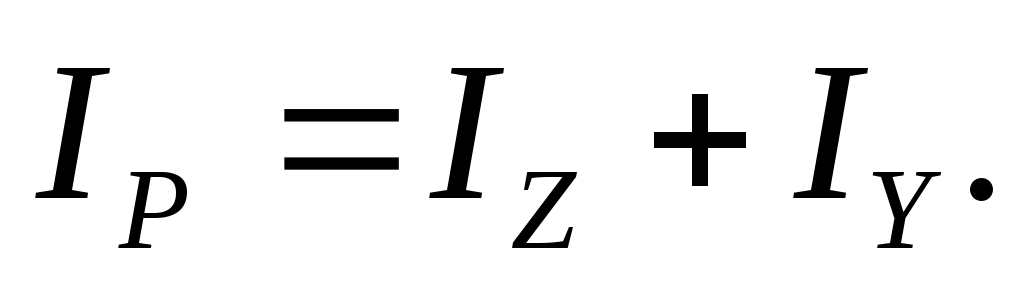 (17.8)
(17.8)
Зависимости между моментами инерции относительно параллельных осей, одна из которых центральная, имеет вид
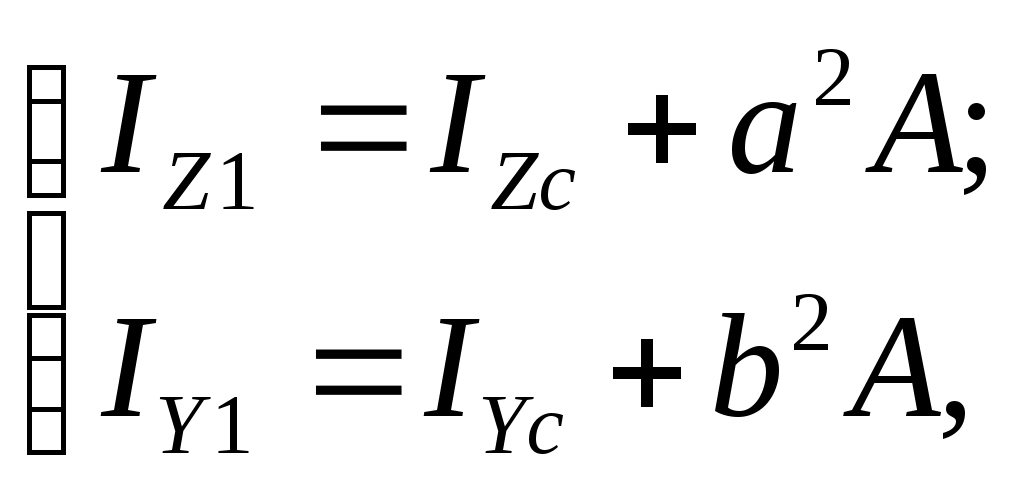 (17.9)
(17.9)
тогда
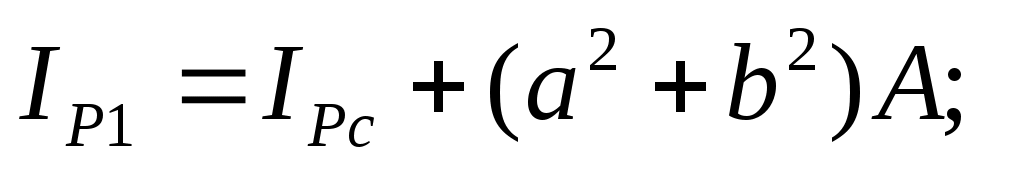 (17.10)
(17.10)
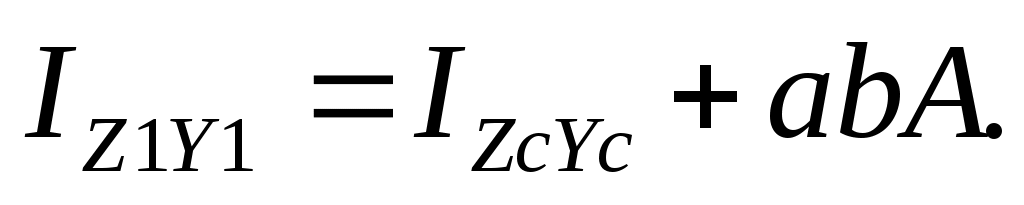 (17.11)
(17.11)
Откуда выводы:
Осевые моменты инерции относительно центральных осей являются минимальными по сравнению с моментами инерции относительно других осей, им параллельным.
При параллельном переносе одной координатной оси (a0, b=0) центробежный момент инерции не изменяется.
Зависимости между моментами инерции при повороте координатных осей вокруг любой точки сечения (рис. 17.2) имеют вид
 (17.12)
(17.12)
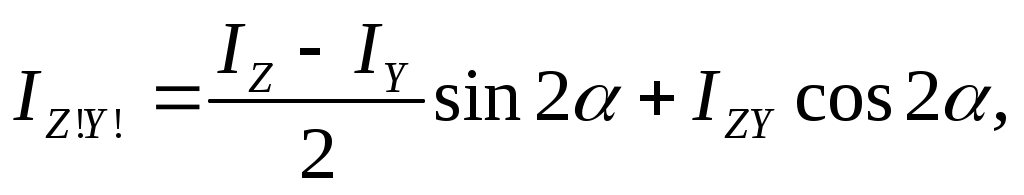 (17.13)
(17.13)
где в (17.12) нижние знаки для IY1; угол положителен, если направлен против часовой стрелки.
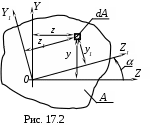 Из анализа формул (17.12), (17.13) следующие выводы.
Из анализа формул (17.12), (17.13) следующие выводы.
Сумма моментов инерции относительно любых взаимно перпендикулярных осей при повороте их вокруг одного и того же начала координат, есть величина постоянная, т.е.
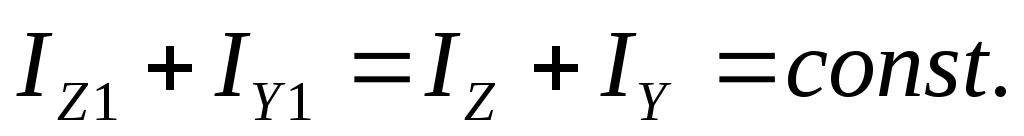
При повороте осей на 900 центробежный момент инерции меняет свой знак.
Так как центробежный момент инерции является непрерывной функцией от угла
, то существует такое значение угла =0, при котором центробежный момент инерции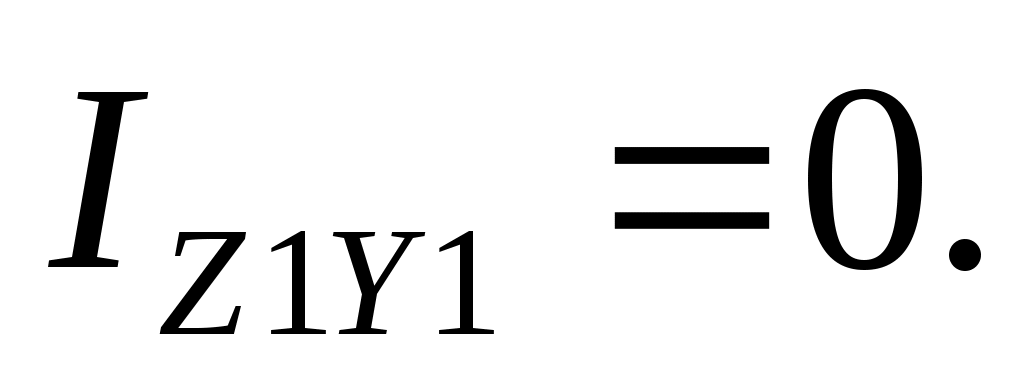 Оси, относительно которых центробежный момент инерции равен нулю, получили название главных осей инерции.
Оси, относительно которых центробежный момент инерции равен нулю, получили название главных осей инерции.
Из (17.13), подставив =0 и приравняв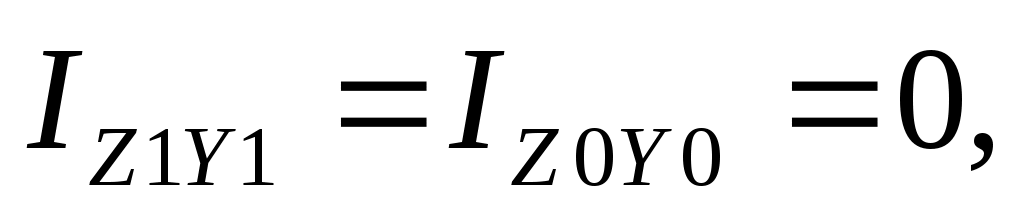 получим формулу для определения положения главных осей инерции
получим формулу для определения положения главных осей инерции
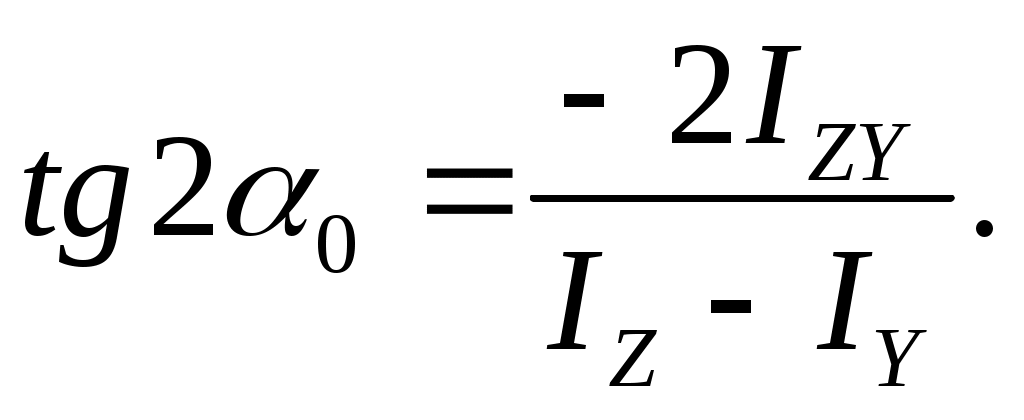 (17.14)
(17.14)
Осевые моменты инерции относительно главных осей называются главными. Главные моменты инерции являются экстремальными, которые принято обозначать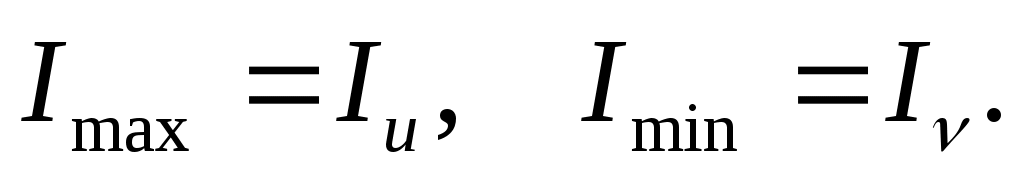
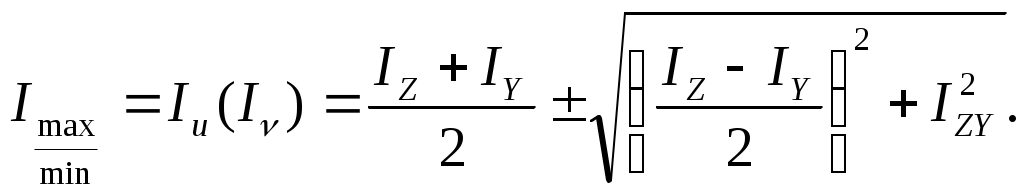 (17.15)
(17.15)
При условии, что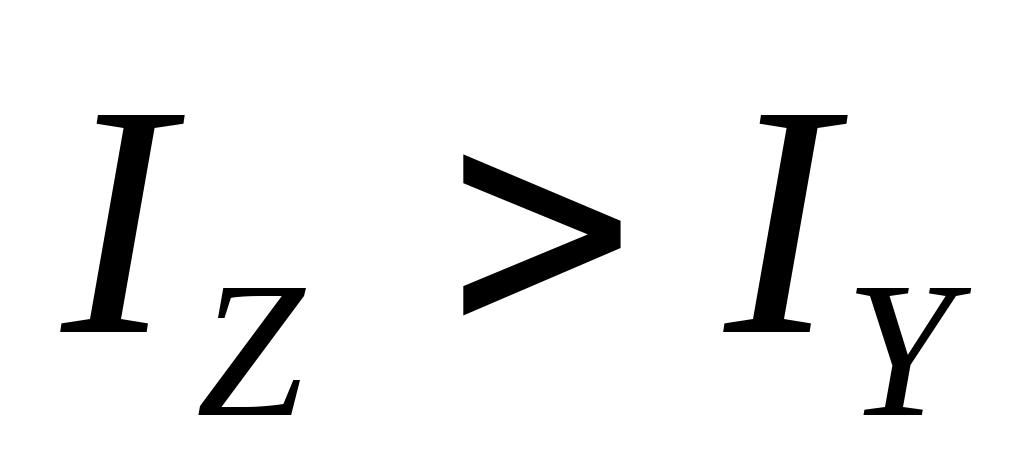 , положение главных осей инерции можно определить и по формуле
, положение главных осей инерции можно определить и по формуле
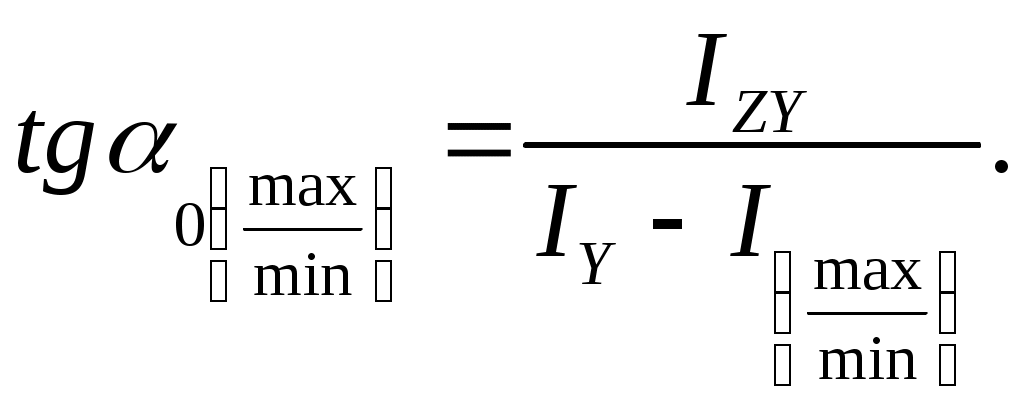 (17.16)
(17.16)
Угол 0, определенный по формулам (17.14) и (17.16), откладывается от оси Z.
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями инерции, а моменты инерции относительно этих осей – главными центральными моментами инерции.
Ось симметрии всегда является главной центральной осью инерции; второй главной осью является любая другая ось, перпендикулярная к оси симметрии.
В сечениях с бесконечным множеством главных центральных осей инерции, начиная с равностороннего треугольника и заканчивая, в пределе кругом (), моменты инерции относительно этих осей равны между собой.
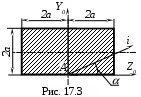 Если моменты инерции относительно главных осей, проходящих через любую точку А сечения равны, то все оси, проходящие через эту точку, являются главными осями и моменты относительно их равны (рис. 17.3).
Если моменты инерции относительно главных осей, проходящих через любую точку А сечения равны, то все оси, проходящие через эту точку, являются главными осями и моменты относительно их равны (рис. 17.3).
С учетом того, что
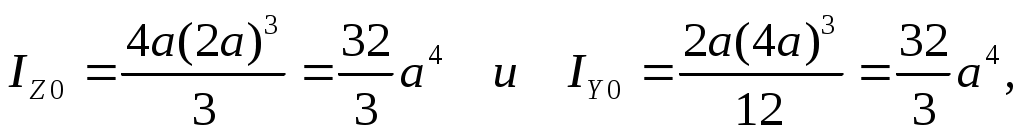
а
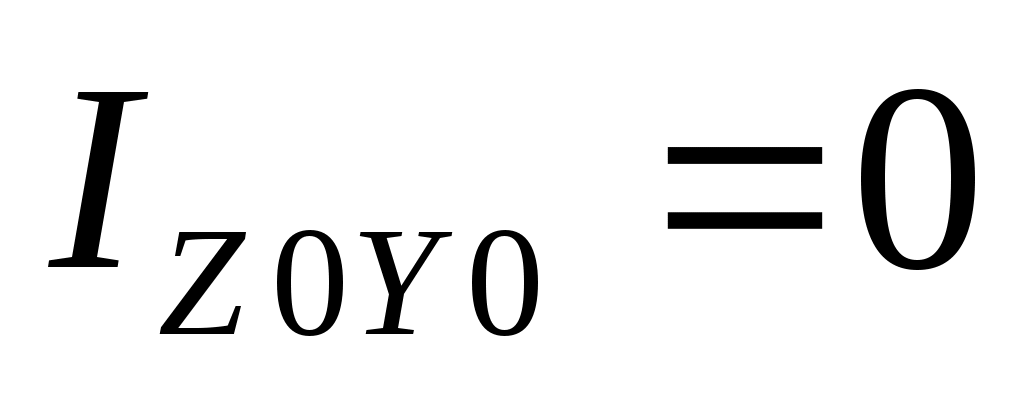 (у0
(у0
Абсолютные размеры детали.
Экспериментально установлено, что размеры детали существенно влияют на величину предела выносливости. С увеличением размеров предел выносливости уменьшается. Так, например, предел выносливости для стали, идущей на изготовление вагонных осей, определенный в лаборатории на образцах диаметром d=7,5 мм, равен 230 МПа. В действительности предел выносливости вагонной оси с диаметром d=170 мм, равен 120 МПа, что почти вдвое меньше лабораторных результатов.
До настоящего времени этому факту нет полного объяснения. Изменение величины предела выносливости в связи с изменением размеров образцов оценивается так называемым масштабным коэффициентом . Масштабным коэффициентом называют отношение предела выносливости детали к пределу выносливости образца диаметром 6 -12 мм.
Внешняя среда.
Усталостная прочность детали зависит от среды, в которой находится деталь. Коррозия среды ( вода, солёная вода, кислоты, пары) резко снижают усталостную прочность. Применение защитных покрытий поверхностей (окраска, металлизация, азотирование, цианирование, цементация, цинкование, плазменное напыление и др.) уменьшает эффект коррозионной среды.
Высокие температуры уменьшают, а низкие несколько повышают усталостную прочность, однако нужно иметь в виду, что при низких температурах резко снижается ударная вязкость.
16.6. Расчёт на прочность при переменных напряжениях
В расчётах на прочность при переменных напряжениях прочность детали принято оценивать по величине фактического коэффициента запаса n,сравнивая его с допускаемым коэффициента запаса [n], устанавливаемым нормами. Условие прочности записывается в виде
n [n].
Коэффициенты запаса n можно определить приближенно с помощью схематизированных диаграмм предельных амплитуд, например, показанной на рис. 16.9, б. Из начала координат проводим луч 01 под углом 1, который соответствует подобным циклам. Точка
М на котором с координатами а и mхарактеризует рабочий цикл. Точка N с координатами nа и nmхарактеризует предельное значение этого же цикла. Таким образом, фактического коэффициента запаса n можно определить как отношение отрезком
ON/OM.
Если луч 01 пересекает прямую АВ, рост напряжений цикла вызывает в образце усталостное разрушение. Коэффициент запаса по отношению к усталостному разрушению в этом случае обозначается nR и определяется из следующих соображений: Точка Nнаходится на прямой АВ и удовлетворяет уравнению (16.13), которое принимает вид
откуда
Получен коэффициент запаса для гладкого образца. Прочность детали зависит от размеров и формы этой детали, от состояния её поверхности. Всё это учитывается соответствующими коэффициентами, в нашем случае эффективным коэффициентом концентрации напряжений k , коэффициентом поверхностной чувствительности, масштабным коэффициентом. Тогда уравнение (16.15) примет вид
коэффициент запаса детали будет равен
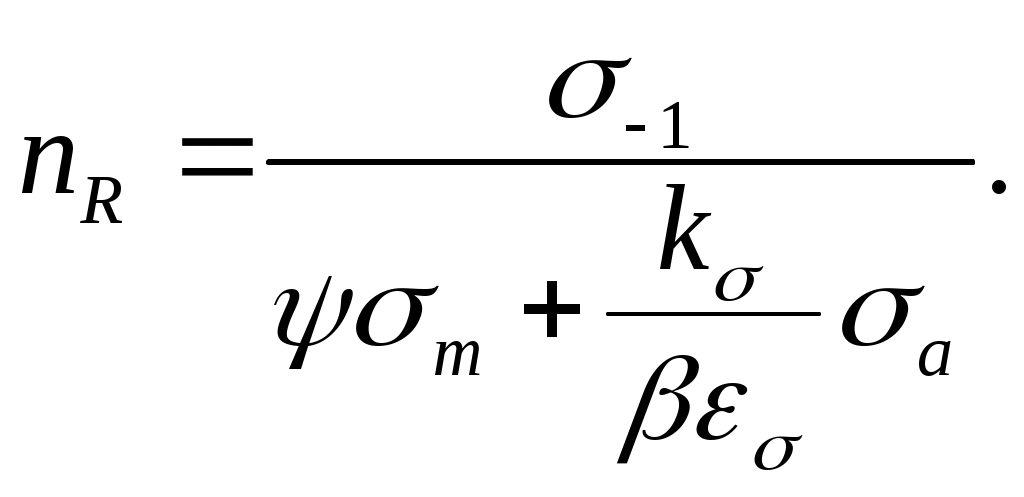 (16.18)
(16.18)Вопросы для самопроверки
1. Что такое усталость материалов?
2. Что такое выносливость ?
3. Как объясняется возникновение трещины усталости в материале?
4. Что такое коэффициент асимметрии?
5. Что такое предел выносливости?
6. Все ли материалы имеют предел выносливости?
7. Какие коэффициенты учитываются при определении коэффициента запаса детали?
17. Геометрические характеристики плоских сечений
17.1. Введение
При решении задач о прочности и жесткости стержней, как было показано, такой характеристики поперечного сечения, как площадь
А, оказалось недостаточно. Так, например, при расчетах стержней на кручение понадобилось ввести понятие полярного момента инерции круглого сечения IPи момента сопротивления того же сечения при кручении WP. В дальнейшем понадобились ещё некоторые новые геометрические характеристики, для которых так же были получены формулы, позволяющие вычислять эти величины в простейших случаях. Однако в инженерной практике нередко приходится иметь дело с более сложными вариантами. В этих случаях сложное сечение представляют в виде фрагментов, вычисляют их геометрические характеристики, а затем по особым законам эти характеристики суммируют. Цель этой главы – ознакомить как с этими законами, так и с некоторыми инженерными рекомендациями, из них вытекающими.
-
Основные положения
К геометрическим характеристикам плоских сечений (рис. 17.1) относятся:
площадь сечения
статический момент площади сечения относительно оси
осевой момент инерции
полярный момент инерции
центробежный момент инерции
Все геометрические характеристики обладают свойством аддитивности.
При рассмотрении плоских сечений оперируют понятием центром масс бесконечно тонкой однородной пластинки постоянной толщины, имеющей то же очертание и размеры, что и данное сечение.
На основании теоремы о моменте равнодействующей
где А- площадь сечения; yc , zc– координаты центра тяжести сечения (ЦТ или С), откуда
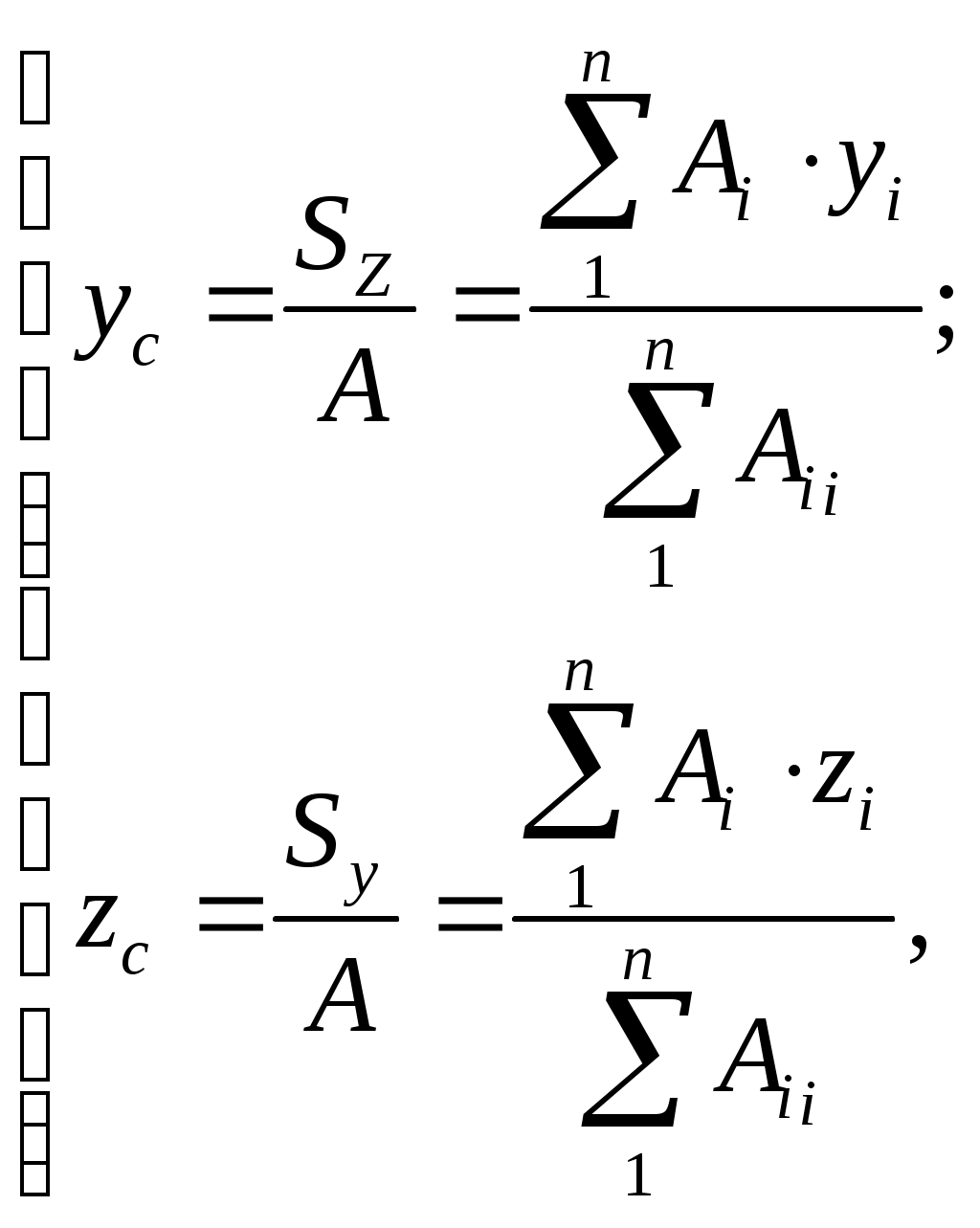 (17.7)
(17.7)где Аi ,уi ,zi– соответственно площади, координаты центра тяжести простых сечений, составляющих данное сложное сечение.
Оси, проходящие через центр тяжести сечения,
называют центральными.
Из (17.6) следует, что если ось Z
с
 овпадает с центральной осью ZС , т.е. ус=0, то SZ= SZc=0,
овпадает с центральной осью ZС , т.е. ус=0, то SZ= SZc=0,откуда выводы:
статический момент площади сечения относительно центральной оси равен нулю;
ось, относительно которой статический момент площади сечения равен нулю, является центральной;
оси симметрии всегда являются центральными.
Так как 2=z 2+y2, то, подставляя 2в (17.4), получим, что
Зависимости между моментами инерции относительно параллельных осей, одна из которых центральная, имеет вид
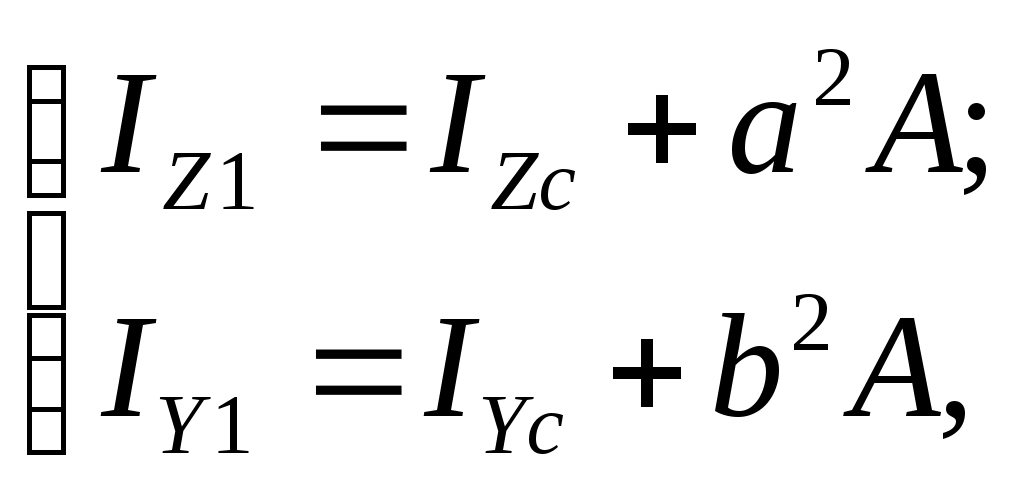 (17.9)
(17.9)тогда
Откуда выводы:
Осевые моменты инерции относительно центральных осей являются минимальными по сравнению с моментами инерции относительно других осей, им параллельным.
При параллельном переносе одной координатной оси (a0, b=0) центробежный момент инерции не изменяется.
Зависимости между моментами инерции при повороте координатных осей вокруг любой точки сечения (рис. 17.2) имеют вид
где в (17.12) нижние знаки для IY1; угол положителен, если направлен против часовой стрелки.
 Из анализа формул (17.12), (17.13) следующие выводы.
Из анализа формул (17.12), (17.13) следующие выводы.Сумма моментов инерции относительно любых взаимно перпендикулярных осей при повороте их вокруг одного и того же начала координат, есть величина постоянная, т.е.
При повороте осей на 900 центробежный момент инерции меняет свой знак.
Так как центробежный момент инерции является непрерывной функцией от угла
, то существует такое значение угла =0, при котором центробежный момент инерции
Из (17.13), подставив =0 и приравняв
Осевые моменты инерции относительно главных осей называются главными. Главные моменты инерции являются экстремальными, которые принято обозначать
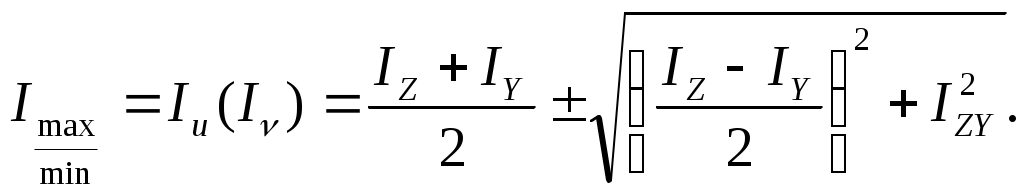 (17.15)
(17.15)При условии, что
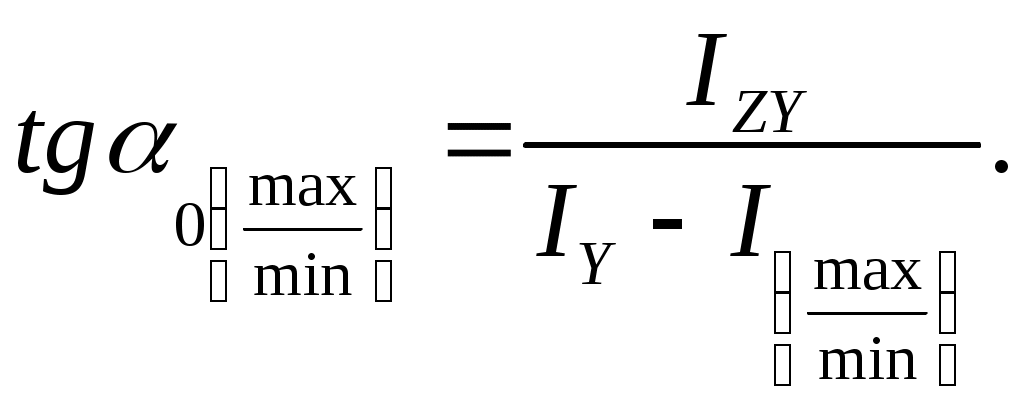 (17.16)
(17.16)Угол 0, определенный по формулам (17.14) и (17.16), откладывается от оси Z.
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями инерции, а моменты инерции относительно этих осей – главными центральными моментами инерции.
Ось симметрии всегда является главной центральной осью инерции; второй главной осью является любая другая ось, перпендикулярная к оси симметрии.
В сечениях с бесконечным множеством главных центральных осей инерции, начиная с равностороннего треугольника и заканчивая, в пределе кругом (), моменты инерции относительно этих осей равны между собой.
 Если моменты инерции относительно главных осей, проходящих через любую точку А сечения равны, то все оси, проходящие через эту точку, являются главными осями и моменты относительно их равны (рис. 17.3).
Если моменты инерции относительно главных осей, проходящих через любую точку А сечения равны, то все оси, проходящие через эту точку, являются главными осями и моменты относительно их равны (рис. 17.3).С учетом того, что
а