Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Зададимся какой-либо другой «похожей» кривой, например параболой



Проверим граничные условия:

при z=0 v(0)=0;

v^’(0)=Cl-2Cz0;

v^’’(0)=2C=const.

z=l v(l)=0;

v^’(l)=Cl-2Cl0;

v^’’(l )=2C=const.
Получили, что v^’’(0)=2C=const и v^’’(l)=2C=const, что означает, что кривизна стержня при потери устойчивости постоянная, в то время она функция параболы т.е. наибольшая кривизна стержня посередине и равная нулю по концам. Учитывая это несоответствие определим F_кр.

Получим вместо

Ошибка равна 20%.

Точность решения может быть резко увеличена, например, если принять, что по закону параболы изменяется не прогиб, а кривизна. Тогда



Проверим граничные условия:

при z=0 М(0)=0 т.е. v^’’(0)=0;
z=l М(l)=0 т.е. v^’’(l)=0.

После интегрирования

;

при z=0.5l ;

;

Получим .

Ошибка равна 0,1%.
Пример 3. Рассмотрим расчетную схему (рис.11.11 ) колонкового бурения с навеса без центратора: т.е. определим критическую силу для защемленного одним концом стержня (низа бурильной колонны), находящегося под действием собственого веса и веса верха бурильной колонны F.

Задаемся уравнением упругой линии изогнутого стержня



Проверим граничные условия:

---

при z=0 v(0)=0;

v^’(0)=(0)=0.

Граничные условия удовлетворяются.

1. Определим энергию изгиба



2. Подсчитаем величину :



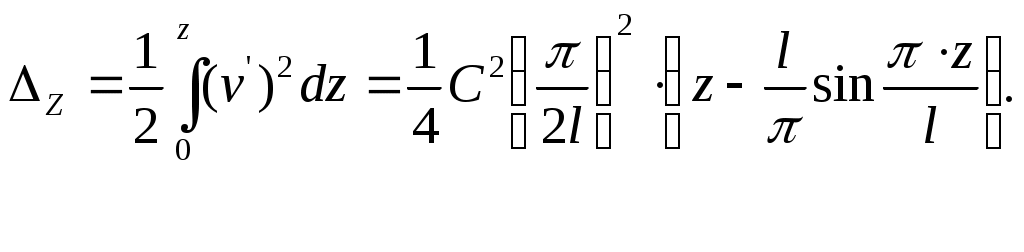
3. Работа сил q:



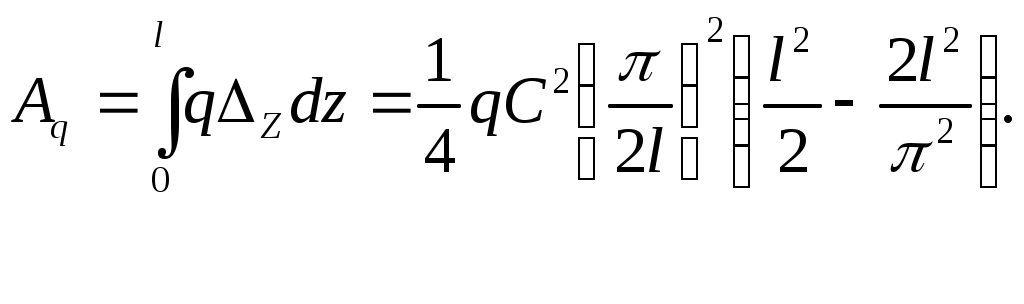
4. Работа силы F:



5. Приравняем работы A_q и A_F к энергии изгиба U и освободимся от постоянной С.



6. Отсюда F_кр= F.

Например: для бурильной трубы D= 96 мм, q= 500 H/м и l=24 м получим F_кр= 63 кН; справочные данные F_кр= 66 кН,  % = 4,5%.

Вопросы для самопроверки

1. 
   Что называется критической силой? Как определяется запас устойчивости?
   
2. 
   Как влияет способ закрепления сжатого стержня на величину критической силы?
   
3. 
   Что называется гибкостью сжатого стержня и как она определяется?
   
4. 
   Что определяет границы применяемости формулы Эйлера?
   
5. 
   Каков метод расчета на продольный изгиб по коэффициенту ?
   
6. 
   Почему процедура энергетического метода предписывает задаться каким-либо правдоподобным уравнением изогнутой оси стержня?
   

12. Тонкостенные сосуды и оболочки

1. 
   Понятие об оболочке
   

Стержень представляет собой особенно часто используемую расчётную модель, но существуют немало важные для практики конструкции, которые по своим геометрическим формам не имеют ничего общего со стержнем и требуют иных приёмов схематизации. Таковы тонкостенные конструкции, крупноразмерные сосуды, ёмкости, резервуары, цистерны, корпуса кораблей, покрытия зданий.
30>

---

Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.

О 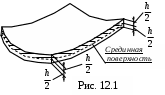болочкой называю тело (рис 12.1), ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина оболочки h) мало по сравнению с другими размерами. Поверхность, делящая толщину оболочки пополам, называется срединной.

Ограничимся рассмотрением оболочек постоянной толщины.

Их геометрия полностью определяется формой срединной поверхности и толщиной оболочки.

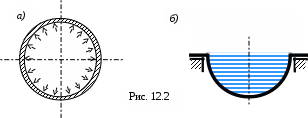
В практике чаще всего встречаются оболочки, срединные поверхности которых – это поверхности вращения (получаются вращением отрезка кривой вокруг некоторой оси), в частности цилиндрические и сферические оболочки (рис.12.2). Такие оболочки называются осесимметричными. В силу симметрии отсутствует сдвиг т.е. 

О
граничимся рассмотрением осесимметричных оболочек.
Предположим, что нагрузка на оболочку также распределена симметрично относительно оси, нормальна к срединной поверхности, непрерывна и не содержит сосредоточенных сил.

Примеры. Сферический сосуд под действием равномерного внутреннего давления газа. Собственным весом стенок и весом газа пренебрегаем (рис. 12.2,а). Полусферический сосуд заполненный жидкостью (рис. 12.2,б).

Если соблюдаются эти три условия, тогда можно принять, что напряжения по толщине постоянные, изгиб отсутствует,  Теория оболочек, построенная в этом предположении, называется безмоментной теорией оболочек.
12.2. Безмоментная теория оболочек. Уравнение Лапласа.

Р
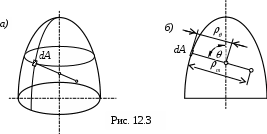
ассмотрим симметричную оболочку толщиною h (рис. 12.3,а).Обозначим через _традиус дуги меридиана срединной поверхности, а через _ - второй главный радиус (рис. 12.3, б), этот радиус равен отрезку нормали.

В

---

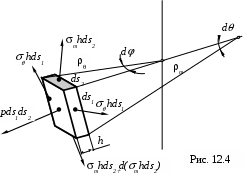
ыделим из оболочки элемент ds₁,ds₂ площадью dA. Будем считать, что на гранях элемента возникают напряжения _ти _.Первое будем называть меридиональным , его вектор направлен по дуге меридиана. Второе _ называется окружным. Напряжения _ти _умноженные на соответствующие площади граней элемента, дадут силы _тhds₂ и_ hds₁ . К этому же элементу приложена сила нормального давления pds₁ds₂ . Проектируя все силы на нормаль, получим

pds₁ ds₂_тhds₂d_ hds₁d=0.

Так как

d= ds₁/_m, d= ds₂/_ ,

то в итоге

(12.1)

Это соотношение известно под названием уравнение Лапласа.


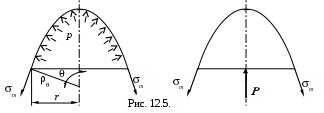
Так как здесь напряжения _ти _неизвестны, то для их определения необходимо составить второе уравнение. И здесь удобнее рассматривать не элемент, а конечную часть оболочки, выделенную коническим сечением. При этом окружные напряжения _ вообще не ‘обнажаться’ и уравнение равновесия будет содержать единственное неизвестное – меридиональное

напряжение _т.
Обозначая через Р осевую равнодействующую внешних сил, получим

_т2 rhsin (12.2)

---

Отсюда определяется меридиональное напряжение _т.

Таким образом, по без моментной теории напряжения _ти _ в оболочке определяются из уравнений равновесия.

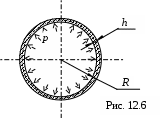Третье главное напряжение, напряжение надавливания между слоями оболочки, предполагается малым и поэтому напряженное состояние оболочки считается двухосным. Рассмотрим расчёт сосудов, под действием внутреннего газового давления, часто встречающихся на практике.

1. Сферический сосуд (рис. 12.6) под действием внутреннего газового давления р.

Для него _т_и h толщина. По условию полной симметрии _т_ .

Формула Лапласа дает:

_т_pR/2h.

Напряженное состояние является двухосным

₁₂pR/2h.

Наименьшее напряжение ₃ принимается равным нулю.
По теории Мора, независимо от величины k ,

_эквМ=₁ - k ₃pR/2h .
По третьей гипотезе прочности:

_эквIII=₁ - ₃ .

Подставляя ₁=pR/2h и ₃  получаем

_эквIII= pR/2h ,

т.е. проверка прочности, как в случае одноосного напряженного состояния.

По четвертой гипотезе прочности:

_эквIV= ,

т.к. ₁₂pR/2h и ₃0, то

_эквIV = pR/2h,

т.е. то же условие, что и по третьей гипотезе прочности.
2. Цилиндрический сосуд.Цилиндрический сосуд, под действием внутреннего газового давления

---