Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Откуда

(16.5)

(16.6)
Установлено, что сопротивление циклическим нагрузкам существенным образом зависит от коэффициента асимметрии цикла.

Коэффициент асимметрии цикла представляет собой отношение
R=_min/_max. (16.7)
Вводится классификация видов циклов в зависимости от значения R.

Центральное место занимает симметричный цикл нагружения,

когда (рис. 16.4).

R= -1, _m =0, _а =_mах= - _min,

так как в условиях симметричного цикла наблюдается наибольшее накопление повреждений в материале изделия.

Различают также знакопеременные и знакопостоянные циклы (рис. 16.4).

Граничными между теми и другими служат отнулевые циклы, когда _min=0, либо _mах=0 (рис. 16.4).


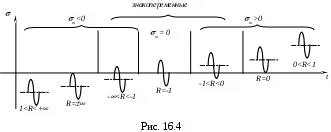
Циклы называются подобными, если они имеют одинаковый коэффициент асимметрии.



16.3. Понятие о пределе выносливости

Надо иметь в виду, что не любые по величине переменные напряжения вызывают усталостное разрушение. Оно может наступить при условии, если переменные напряжения в той или иной точке детали превзойдут свое критическое значение, называемое пределом выносливости (усталости).

Пределом выносливости называют наибольшее значение максимального напряжения цикла _mах( или _min, если _mах < _min), которое не вызывает усталостного разрушения детали при неограниченно большом числе циклов. Предел выносливости обозначается _R, где R- коэффициент асимметрии цикла.

П ри симметричном цикле предел выносливости обозначается _-1 , при простом растяжении и сжатии - ₊₁ , а при отнулевом - ₀ . При симметричном цикле предел выносливости _-1 меньше по сравнению с пределами выносливости других видов циклов, а определение его значительно проще

---

, чем при других циклах.

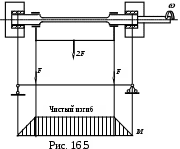
Для опытного определения _-1 на рис. 16.5 представлена схема одной из многих машин. Образец закрепляют в машине так, чтобы средняя часть образца подвергалась чистому изгибу, как это показано на эпюре моментов M( рис. 16.5 ).

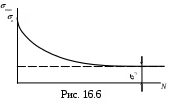
Каждое волокно образца, вращаемого в машине, при повороте его на 180⁰ будет попеременно то растянуто ,то сжато. Задавая образцам различные величины напряжений _mах цикла, определяют число циклов, необходимое для доведения образца до разрушения. По результатам опыта строят кривую выносливости _mах=f(N) ( где _mах – максимальное напряжение цикла,

N число циклов, при котором произошло разрушение образца ) (рис.16.6). Из этого рисунка видно, что кривая _mах=f(N) асимптотически приближается к оси абсцисс. Ордината '' горизонтальной '' асимптоты этой кривой при таком испытании будет равна пределу выносливости _-1 .

Опыты показали, что если образец не разрушается, например, после 10⁷ оборотов, то он не разрушится и при большем числе оборотов. Поэтому испытание образцов прекращается для черных металлов после 10⁷ оборотов «база испытаний», для цветных металлов – после 10⁸ . Кривые выносливости для цветных металлов не имеют асимптот, и ординаты их с ростом числа оборотов падают до нуля.

16.4. Диаграмма предельных амплитуд
Экспериментально установлено, что предел выносливости при асимметричном цикле больше, чем при симметричном, и зависит от степени асимметрии цикла: R=_min/_max.

При графическом изображении зависимости предела выносливости от коэффициента асимметрии необходимо для каждого R определить свое значение предела выносливости. Опытное определение _R для каждого вида цикла из-за большого числа образцов и длительного времени их испытания почти невозможно. Поэтому по ограниченному числу опытов для трех- четырех значений R строят диаграмму предельных циклов.

Предельным циклом называют такой, у которого максимальное напряжение равно пределу выносливости, т.е. _max=_R .

По оси ординат откладывают значение амплитудного _а

---

, а по оси абсцисс – среднего _m напряжения предельного цикла. Каждая пара напряжений _аи _m , определяющая предельный цикл, изображается точкой на диаграмме (рис. 16.7). Опыты показывают, что эти точки в общем случае располагаются на кривой АВ, которая на оси ординат отсекает отрезок, равный пределу выносливости симметричного цикла _-1 (при этом цикле _m =0), а оси абсцисс – отрезок, пределу прочности _в . В этом случае действуют постоянные во времени напряжения:

_min= _max = _в =₊₁ . (16.8)


Т 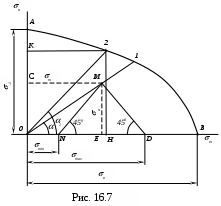аким образом, диаграмма предельных циклов характеризует зависимость между величинами средних напряжений и величинами предельных амплитуд цикла. Любая точка М, расположенная внутри этой диаграммы, соответствует некоторому циклу, определяемому величинами _m(СМ) и_а(МЕ). Для определения _max ,_min цикла из точки М проводят отрезки MNи MD

до пересечения с осью абсцисс под углом 45⁰ к ней. Тогда (рис. 16.7):

NE=EM=ED=_a;

_max=OD=OE+ED=_m+_a;

_min=ON=OE - NE=_m-_a.

Подобные циклы будут характеризоваться точками, расположенными на прямой 01, угол наклона которой определяется формулой

tg=_a /_m.

Тогда точка 1 соответствует предельному циклу из всех указанных подобных циклов. С помощью диаграммы можно определять предельные напряжения для любого цикла, например, для пульсирующего ( отнулевого) _R =₀ , у которого

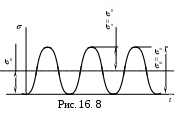
_min =0, а _а =_m=_mах /2_min (рис. 16.4, рис. 16.8). Для этого из начала координат (рис. 16.7) проводят прямую по углом ₁ = 45⁰ до пересечения с кривой в точке 2. Координаты этой точки: ордината Н 2 равна предельному амплитудному напряжению, а абсцисса К 2 – предельному среднему напряжению этого цикла.

Предельное максимальное напряжение пульсирующего цикла равно сумме координат точки 2:

---

(16.9)

Подобным образом можно решать вопрос о предельных напряжениях любого цикла.

Если деталь машины, испытывающая переменные напряжения, изготовлена из пластичного материала, то опасным будет не только усталостное разрушение, но и возникновение пластических деформаций. Максимальное напряжение цикла в этом случае определяются равенством

(16.10)

где _Т – предел текучести.


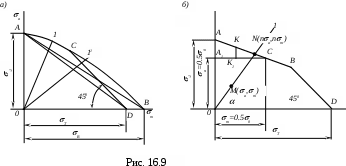
Точки, удовлетворяющие этому условию, располагаются на прямой DC, наклоненной под углом 45⁰ к оси абсцисс (рис. 16.9,а) , так как сумма координат любой точки этой прямой равна _Т .
Если прямая 01(рис. 16.9,а) , соответствующая данному виду цикла, при увеличении нагрузок на деталь машины пересекает кривую АС, то произойдёт усталостное разрушение детали. Если же прямая 01¹ пересекает СD, то деталь выйдет из строя в результате появления пластических деформаций.

Часто на практике пользуются схематизированными диаграммами предельных амплитуд. Кривую ACD(рис. 16.9,а) для пластических материалов приближенно заменяют прямой AD. Уравнение её имеет вид

(16.11)

Для хрупких материалов диаграмму ограничивают АВ с уравнением

(16.12)

Наибольшее распространение получили диаграммы предельных амплитуд, построенные по результатам трех серий испытаний образцов: при симметричном цикле _-1 (точка А), при отнулевом цикле (точка С) и статическом разрыве _Т (точка D) (рис. 16.9,б). Составим уравнение прямой АВ. Возьмём на прямой точку К(^_а , ^_m). Из подобия треугольников АСА₁ и КСК₁ получим уравнение прямой АВ в виде

(16.13)

где

---

16.5. Факторы, влияющие на величину предела выносливости

На величину предела выносливости влияют многие факторы. Рассмотрим влияние наиболее важных из них, которые обычно учитываются при оценке усталостной прочности.

Концентрация напряжений. Усталостные трещины, как правило, возникают в местах концентрации напряжений.

Степень концентрации напряжений оценивается коэффициентами концентрации. Различают теоретический _и эффективный k_коэффициенты концентрации.

Эффективный коэффициент концентрацииk_ ,учитывающий реальные особенности материала, меньше теоретического ₀. Снижение эффекта концентрации напряжений за счет реальных свойств материала при циклических нагрузках оценивается коэффициентом чувствительности q, который равен

. (16.14)

Чем выше механические свойства стали, тем больше коэффициент чувствительности q. Для высокопрочных сталей q 1. Это значит, что нет разницы между теоретическим _и эффективным k_коэффициентом концентрации.

Для углеродистых сталей q≈0,6 – 0,8, для чугуна q=0.
Качество поверхности детали.

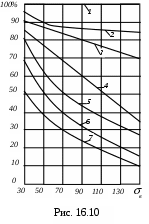На рисунке 16.10 приведены данные зависимости предела выносливости от состояния поверхности образца. Предел выносливости образца с полированной поверхностью принят за 100% (прямая 1). Кривая 2 относится к шлифованной поверхности, а кривая 3 – к поверхности при обработке резцом. Кривая 4 соответствует поверхности, на которую нанесена насечка. Кривая 5 соответствует поверхности, полученной при прокатке. Кривые 6 и 7 относится к поверхности, корродированной соответственно в обычной и морской воде. Как видим, более грубая поверхность детали создает дополнительные места концентрации напряжений и, следовательно, более благоприятные условия для появления микротрещин. Именно поэтому наиболее ответственные детали механизмов и машин часто полируют. Качество поверхностного слоя оценивается коэффициентом поверхностной чувствительности

---