Файл: 2 Передаточные числа трансмиссии 1 Примем стандартное передаточные число главной передачи u.docx

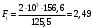кН;

8) Единичное контактное напряжение Z_H:

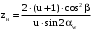; 822282\* MERGEFORMAT (2...)

На первой передаче:



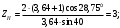
9) Единичное напряжение изгиба Y_F:

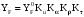; 832283\* MERGEFORMAT (2...)

;

;

.

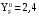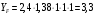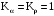10) Коэффициент K_u, учитывающий параметры парного зубчатого колеса:

K_u = 1,37.

11) Коэффициент K_ρ, учитывающий перераспределение толщин зубьев шестерни и колеса:

K_ρ = 1.

12) Коэффициенты Z_∑ и Y_∑, зависящие от суммарной длины контакта линий и перекрытия зубьев:

Z_∑ = Y_∑ = 1,1;

13) Коэффициенты K_Hα и K_Fα, учитывающие распределение нагрузки между зубьями:

K_Hα = K_Hψ · K_Hv

K_Hα = K_Fα = 1.

14) Коэффициенты K_Hβ, K_Fβ неравномерности распределения нагрузки по ширине венца в процессе эксплуатации:

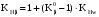; 842284\* MERGEFORMAT (2...)

.

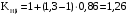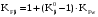; 852285\* MERGEFORMAT (2...)

.

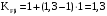15) Коэффициенты K_Hv и K_Fv, учитывающие динамическую нагрузку в зацеплений:

;

.

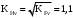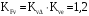16) Коэффициенты K_Hμ и K_Fμ учитывающие свойства применяемого смазочного материала характерны работы зубчатого колеса в передаче:

K_Hμ = 1;

K_Fμ = 1,05.

17) Значение параметра предела контактной выносливости П_Hlimb предела выносливости при изгибе 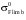: Сталь 18ХГТ;

П_Hlimb = 18 МПа; 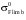= 370 МПа;mH = 3, mF = 9, N_HO = 1,2 · 10⁸, N_FO = 4 · 10⁶ циклов.

18) Коэффициенты K_Hx и K_Fx, зависящие от размеров зубчатого колеса:

K_Hx = 1;

K_Fx = 1.

19) Коэффициенты Z_R и Y_R учитывающие особенности обработки зубьев:

---

Y_R = 1;

Z_R = 0,88.

20) Коэффициент K_FC, учитывающий характер нагружения зубчатого колеса:

K_FC = 1,3.

21) Относительный пробег на различных передачах

Предварительно находим γ_р и γ_срi

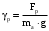; 862286\* MERGEFORMAT (2...)

F_р ≤ F_φ = m_agφ; 872287\* MERGEFORMAT (2...)

где φ = 0,7.

F_φ = 1578· 9,81 · 0,7 = 10,8 кН;

F_Р = 10,8 кН;

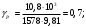882288\* MERGEFORMAT (2...)

22) Среднее значение удельных окружных сил γ_срi:

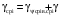; 892289\* MERGEFORMAT (2...)

На первой передаче:

γ_cp1 = γ_ψcp1 = 0,4;

γ_в.cp1 = 0, т. к. v_ср1 < 40 .

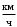По таблице определим: K_пН и К_пF



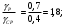
Следовательно: K_пН = 0,2; К_пF = 0,1.

23) Определение расчётных напряжений

Расчётное напряжение изгиба σF, МПа σ_F, МПа:

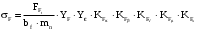; 902290\* MERGEFORMAT (2...)

где b_f – рабочая ширина зубчатого венца, мм.

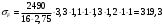МПа;

25) Предельное напряжение изгиба 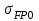, МПа:

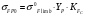; 912291\* MERGEFORMAT (2...)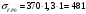



26) Ресурс по усталости при изгибе обеспечивающий 1 км пробега R_1F.

; 922292\* MERGEFORMAT (2...)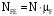

; 932293\* MERGEFORMAT (2...)

V_ср = 27,3 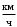, то 1 км μ_F = 0,6, т.к. на данной передаче автомобиль проедет за 3,7 минут;

n = 181,9 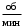, то N = 181,9·3,7 = 667,02 циклов;

N_1FE =667,02 ·0,6 = 400,2 циклов;

R_1F = 319,3⁹ · 400,2 ∙0,7/100 = 9,5 ·10²²;

27)Общий ресурс зубчатого колеса R_Flimb:

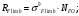942294\* MERGEFORMAT (2...)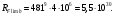



28) Пробег автомобиля до усталостной поломки зуба L

---

_F, км:

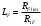; 952295\* MERGEFORMAT (2...)

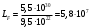км;

29) Допускаемые напряжения изгиба σ_FP, МПа:

σ_FP = σ_FPO · k_FL; 962296\* MERGEFORMAT (2...)

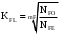; 972297\* MERGEFORMAT (2...)

где 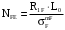; 982298\* MERGEFORMAT (2...)

L₀ – пробег до капитального ремонта 125 тыс. км.

;



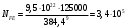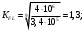
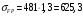МПа;

0,6 σ_FlimM=0,6∙3800=2280 МПа.

т.к. σ_FP < 0,6 σ_FlimM => σ_FP = 625,3МПа;

30)Установление относительных пробегов.

На основании экспериментальных исследований было установлено, что изменение скорости движения автопоезда для дорожных условий нашей страны приближенно может быть описано нормальным законом распределения (рис.9):

;

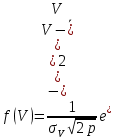992299\* MERGEFORMAT (2...)

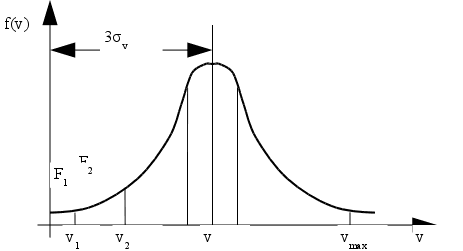
Рис. 9 - Кривая распределения скоростей движения автопоезда

Для проектируемого автомобиля считаем

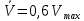	;	10022100\* MERGEFORMAT (2...)
	;
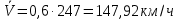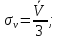		10122101\* MERGEFORMAT (2...)

---

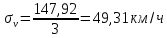Все результаты вычислений заносим в таблицу 12.

Кривая f(V) является усеченной как по минимальному V = 0, так и по максимальному V_max значениям скоростей.

Находим средние скорости движения автомобиля на высшей и i-ой передачах в коробке скоростей:

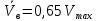		10222102\* MERGEFORMAT (2...)
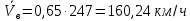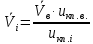		10322103\* MERGEFORMAT (2...)

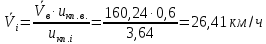Определяем квантили нормального распределения характеризующие разности  в долях среднего квадратического отклонения  .

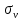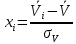		10422104\* MERGEFORMAT (2...)

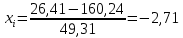По таблицам функции нормального распределения для каждого x_i находим площадь под той частью кривой нормального распределения, которая расположена левее координаты v_i :

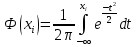10522105\* MERGEFORMAT (2...)

Считаем, что разность F_i двух смежных значений Ф(x_i) и Ф(x _{i - 1}) пропорциональна относительному пробегу на i-ой передаче в коробке передач (кроме высшей). Для i = 1 Ф(x _{i - 1}) = 0.

Находим удельную силу тяги на колесах при включенной высшей передаче:

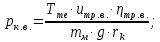		10622106\* MERGEFORMAT (2...)

---

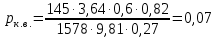где u_тр.в = u_min при включенной высшей передаче на режиме максимального крутящего момента двигателя.

Определяем коэффициент тяги К_т , учитывающий влияние тяговых качеств проектируемого автопоезда на характер кривой распределения скоростей и относительные пробеги на передачах:

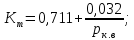		10722107\* MERGEFORMAT (2...)

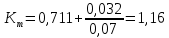Находим относительные пробеги на различных (кроме высшей) передачах:

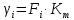		10822108\* MERGEFORMAT (2...)
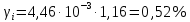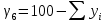		10922109\* MERGEFORMAT (2...)

---