Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4607
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
1. Найдите:
а) Общее решение дифференциального уравнения
b) частное решение дифференциального уравнения пункта (а), учитывая следующие условия: у(0) =2, у’=2, x=0
2.Скорость остывания воды в чайнике пропорциальна разности температуры чайника и температуры кухни 20 0С. Чайник выключился в 10.20 при температуре воды 1000С, в 10.30 температура воды в чайнике было 80 0С
а) Запишите общее уравнение охлаждения тела по заданным условиям.
b) Выясните, когда температура воды в чайнике будет равно 400С?
-
Частица совершает простое гармоническое движение. Отклонение от центра колебания частицы равно x метрам за время t секунд.
-
Покажите, что x = Acos4t + Bsin4t является общим решением дифференциального уравнения
-
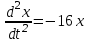
x=2 при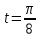
, а 
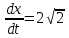
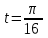. Найдите значение А и В.
-
Найдите наименьшее положительное значение t, при котором скорость частицы равна нулю. Ответ запишите до 3 значащих цифр.
Схема выставления баллов 3 вариант
| № | Ответ | Балл | Дополнительная информация |
| 1a | k 2+2k+10=0 | 1 | |
| D <0 | 1 | | |
 | 1 | | |
| y=C1e –xcos3x+C2e-xsin3x | 1 | | |
| 1b | y’ =e x (C1cos3x+C2sin3x)- e x (3C1sin3x-3C2cos3x) | 1 | |
| При условии, что y(0)=2, C2=2 | 1 | | |
| При условии, что y’ \(0)=2, C=0 | 1 | | |
| y=2sin3x ex | 1 | | |
| 2a |   | 1 | |
 | 1 | Видно или подразумевается | |
| | 1 | Балл выставляется за верное интегрирование одной из функций | |
| T = C1ekt + 20 или эквивалент | 1 | Не принимается ответ с С | |
| 2b | При t =0, C1 = 80 | 1 | |
| При t =10, T = 600,  | 1 | Или эквивалент | |
| При T = 400, 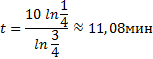 | 1 | | |
| 3a |  | 1 | |
 | 1 | | |
 | 1 | | |
| 3b | B = 2 | 1 | |
| A=1 | 1 | Или эквивалент | |
| 3c | v = x' или -4 A sin 4t + 4B cos 4t = 0 | 1 | |
| tg4t = k | 1 | Принимается ответ со своими значениями A и B | |
| tg4t =2 | 1 | | |
| 4t = arctg2 | 1 | | |
| t = 0,276 | 1 | | |
| Итого: | | 25 | |
4 ВАРИАНТ
| Оценивание заданий работы | |||
| № задания | 1 | 2 | 3 |
| Количество баллов | 8 | 7 | 10 |
| Всего баллов | 25 балла | ||
-
. Найдите:
а) Общее решение дифференциального уравнения
-
частное решение дифференциального уравнения пункта (а), учитывая следующие условия: у(0) =1, у’=1, x=0
-
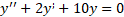
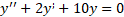В воде, температура которой 20 С, в течении 10 мин тело охлаждается от 100 С до 60 С.
-
Запишите общее уравнение охлаждения тела по заданным условиям.
-
За какое время тело охладится до 30 С, если по закону Ньютона скорость охлаждения пропорциональна разности температур тела и охлаждающей среды?
-
Частица совершает простое гармоническое движение. Отклонение от центра колебания частицы равно x метрам за время t секунд.
-
Покажите, что x = Acos2t + Bsin2t является общим решением дифференциального уравнения
-
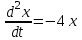
x=2 при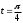
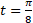
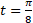, а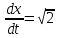 
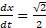
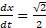. Найдите значение А и В. -
Найдите наименьшее положительное значение t, при котором скорость частицы равна нулю. Ответ запишите до 3 значащих цифр.
Схема выставления баллов 4 вариант
| № | Ответ | Балл | Дополнительная информация |
| 1a | k 2 -4k +5 0 | 1 | |
| D <0 | 1 | | |
 | 1 | | |
| y=e2x(C1 cosx+C2sinx | 1 | | |
| 1b | y’ =e 2x (C1cosx+C2sinx)- e 2x (C1sinx-C2cosx) | 1 | |
| При условии, что y(0)=2, C2=1 | 1 | | |
| При условии, что y’ \(0)=2, C=0 | 1 | | |
| y=e2xsinx | 1 | | |
| 2a | | 1 | |
| | 1 | Видно или подразумевается | |
| | 1 | Балл выставляется за верное интегрирование одной из функций | |
| T = C1ekt + 20 или эквивалент | 1 | Не принимается ответ с С | |
| 2b | При t =0, C1 = 80 | 1 | |
| При t =10, T = 600,  | 1 | Или эквивалент | |
| При T = 300, 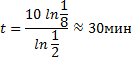 | 1 | | |
| 3a |  | 1 | |
 | 1 | | |
 | 1 | | |
| 3b | B = 2 | 1 | |
| A=1 | 1 | Или эквивалент | |
| 3c | v =x' или -2 A sin 2t +2B cos 2t = 0 | 1 | |
| tg2t = k | 1 | Принимается ответ со своими значениями A и B | |
| tg2t =2 | 1 | | |
| 2t = arctg2 | 1 | | |
| t = 0,553 | 1 | | |
| Итого: | | 25 | |