Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.11.2023

Просмотров: 4616

Скачиваний: 247

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ

ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ

ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»

РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ

ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ

ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ

Количество баллов – 25

Схема выставления баллов

Схема выставления баллов

Схема выставления баллов

Схема выставления баллов


ЗАДАНИЯ

Оценивание заданий работы

№ задания
1
2
3

Количество баллов
4
8
4

итого
16 баллов

1 ВАРИАНТ

1. а) Определите по развертке тело.



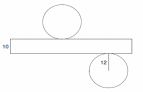
b) Вычислите площади боковой и полной поверхности

3. Сфера задана уравнением (x+1)2 + y2 +(z-3)2 = 25.

а) Покажите, что точка A(-1;3; -1) принадлежит сфере.

  1. Запишите координаты вектора ОА, где О — центр сферы.

  2. Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку А

  3. Найдите расстояние от центра сферы до плоскости 2x- y+2z-5=0 и определите взаимное расположение сферы и данной плоскости.

  1. Периметр осевого сечения конуса равен 9 см, а угол развертки боковой поверхности 450. Найдите высоту конуса.


2 ВАРИАНТ

  1. а) Определите по развертке тело.


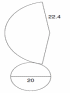
b) Вычислите площади боковой и полной поверхности


  1. Сфера задана уравнением x2 + (y-2) 2 +(z-3)2 = 16.

а) Покажите, что точка В(0;2; -1) принадлежит сфере.

  1. Запишите координаты вектора ОВ, где О — центр сферы.

с) Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку В.

  1. Найдите расстояние от центра сферы до плоскости x- y+z-1=0 и определите взаимное расположение сферы и данной плоскости.

  1. Периметр осевого сечения конуса равен 18 см, а угол развертки боковой поверхности 900 . Найдите высоту конуса.

  1. ВАРИАНТ

  1. а) Определите по развертке тело.


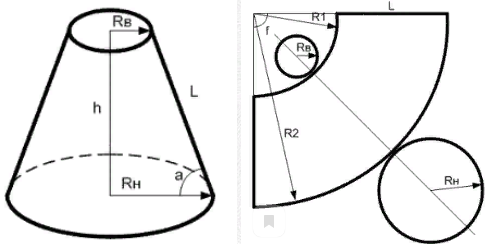
b) Вычислите площади боковой и полной поверхности, если L=8 см, RB = 3см, RH =6 см.

  1. Сфера задана уравнением (x+2)2 + (y-1) 2 +z2 = 9.

а) Покажите, что точка С(1;1; 0) принадлежит сфере.

  1. Запишите координаты вектора ОС, где О — центр сферы.

  2. Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку С.

  3. Найдите расстояние от центра сферы до плоскости x+ y-z-2=0 и определите взаимное расположение сферы и данной плоскости.

  1. Периметр осевого сечения конуса равен 12 см, а угол развертки боковой поверхности 600 . Найдите высоту конуса.




  1. ВАРИАНТ

  1. а) Определите по развертке тело.


b) Вычислите площади боковой и полной поверхности, если L=10 см, RB = 5см, RH =7 см.


  1. Сфера задана уравнением (x-3)2 + (y+4) 2 +z2 = 25.

  1. Покажите, что точка D(3;1; 0) принадлежит сфере.

b) Запишите координаты вектора ОD, где О — центр сферы.

с) Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку D.

  1. Найдите расстояние от центра сферы до плоскости 2x+ y-z-1=0 и определите взаимное расположение сферы и данной плоскости.

  1. Периметр осевого сечения конуса равен 6 см, а угол развертки боковой поверхности 300 . Найдите высоту конуса.




Критерий оценивания
№

задания
Дескриптор
Балл

Обучающийся

Распознает развертки тел вращения.
1 a
записывает название фигуры на первом рисунке;
1

Находит площадь

поверхности конуса и площадь поверхности

цилиндра.
1 b
определяет радиус окружности;
1

находит площадь поверхности цилиндра;
1

находит площадь поверхности конуса;
1

Решает задачи на

взаимное расположение плоскости и сферы в координатах.
2
показывает принадлежность точки А сфере;
1

указывает координаты центра сферы;
1

находит координаты вектора ОА;
1

подставляет координаты вектора-

нормали в общее уравнение плоскости;
1

подставляет координаты точки А в общее уравнение плоскости;
1

записывает общее уравнение плоскости;
1

применяет формулу расстояния от точки до плоскости;
1

находит расстояние и делает вывод о взаимном расположении сферы и плоскости;
1

Находит элементы конуса.
3
использует периметр сечения и выражает через неизвестную радиус и образующую конуса;
1

использует формулу для нахождения длины дуги, составляет уравнение;
1

находит радиус и образующую конуса;
1

находит высоту конуса.
1

Итого:
16
1   ...   35   36   37   38   39   40   41   42   ...   59

Смотрите также файлы