Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4613
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «ОБЪЁМЫ ТЕЛ»
ФИ ОБУЧАЮЩЕГОСЯ ___________________________________________________________
| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Использует формулу объёма призмы. | Затрудняется в использовании формулы объёма призмы. | Определяет объём параллелепипеда, затрудняется определить изменение объёма призмы. | Применяет формулу объёма призмы при решении задач. |
| Находит объём цилиндра и объём части шара. | Затрудняется в нахождении объёма цилиндра /шара. | Применяет формулы для нахождения объёма цилиндра и объёма полушара, допускает вычислительные ошибки. | Вычисляет объём цилиндра и объём части шара. |
| Применяет свойство объёмов пространственных фигур. | Затрудняется в применении свойств объёмов пространственных фигур. | Показывает отношение объёмов подобных фигур, допускает ошибки при определении линейных размеров. | Решает задачу на применение свойств объёмов пространственных фигур. |
| Находит объём усеченной пирамиды. | Затрудняется в нахождении объёма усеченной пирамиды. | Применяет формулу объёма усеченной пирамиды, допускает ошибки при нахождении элементов пирамиды. | Вычисляет объём усеченной пирамид |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Обзор суммативного оценивания
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 7 заданий, включающие вопросы с множественным выбором ответов, требующие краткого и развернутого ответов.
В заданиях с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.
В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующие развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приёмы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Количество заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Многогранники | 11.1.2 знать определение многогранника и его элементов | Знание и понимание | 1 | 1 | МВО | 2 мин | 1 | 20 |
| 11.3.3 решать задачи на нахождение элементов многогранников | Применение | 3 | 2b | КО | 4 мин | 2 | ||
| 3a | РО | 12 мин | 7 | |||||
| 4b | РО | 8 мин | 5 | |||||
| 11.3.1 выводить формулы площади боковой и полной поверхности призмы и применять их при решении задач | Применение | 1 | 3b | РО | 8 мин | 2 | ||
| 11.1.4 знать определение пирамиды, ее элементов, виды пирамид; уметь изображать их на плоскости | Знание и понимание | 1 | 2a | КО | 3 мин | 2 | ||
| 11.2.4 определять расположение проекции вершины пирамиды на плоскость основания | Применение | 1 | 4a | КО | 3 мин | 1 | ||
| ИТОГО: | | | 7 | | | 40 мин | 20 | 20 |
ЗАДАНИЯ
| Разбаловка заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 1 | 4 | 9 | 6 |
| итого | 20 баллов | |||
1 ВАРИАНТ
1. Определите вид многогранника, изображенного на рисунке:
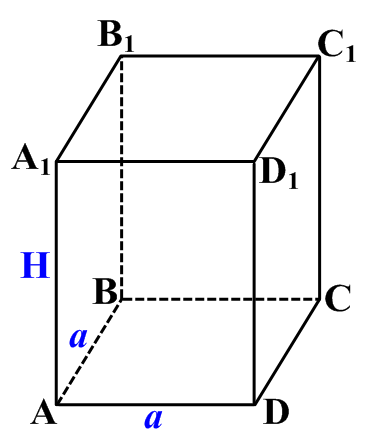
А) прямоугольный параллелепипед;
В) прямая четырёхугольная призма;
С) правильная четырёхугольная призма;
D) параллелепипед.
2. а) Изобразите правильную треугольную призму. Изобразите диагональ боковой грани призмы.
b) Диагональ боковой грани призмы равна 10 см, а сторона основания равна 6см. Найдите высоту призмы.
3. В прямом параллелепипеде стороны основания равны 6см и 8см, а один из углов основания равен 60°. Высота призмы равна 10
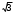 см. Выполните рисунок по условию задачи.
см. Выполните рисунок по условию задачи.а) Найдите большую диагональ параллелепипеда .
b) Вычислите площадь полной поверхности параллелепипеда.
4. Во время строительства пирамидального здания была собрана конструкция с учётом того, что две его стены должны быть перпендикулярны прямоугольному основанию здания.
а) Изобразите конструкцию. Укажите на изображении точку, в которую проектируется вершина пирамиды.
b) Стороны основания пирамиды равны 20м и 15м. Боковое ребро пирамиды, противоположное её прямому двугранному углу, наклонено к основанию под углом 45°. Найдите высоту пирамиды.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | С | 1 | |
| 2а | 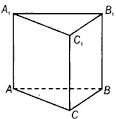 | 1 | |
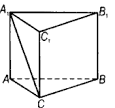 | 1 | Принимается альтернативное решение | |
| 2b | Длина высоты призмы вычисляется по теореме Пифагора 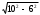 | 1 | |
| 8 см | 1 | | |
| 3а | Выполнен рисунок по условию задачи. | 1 | |
| Указано, что основанием параллелепипеда является параллелограмм. | 1 | | |
| Найден второй угол параллелограмма 120° | 1 | | |
| Длина большей диагонали параллелограмма вычисляется по теореме косинусов 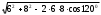 | 1 | | |
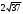 см см | 1 | | |
| Длина большей диагонали параллелепипеда вычисляется по теореме Пифагора 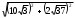 | 1 | | |
| 8 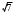 см см | 1 | | |
| 3b | 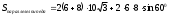 | 1 | |
| 328 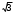 см² см² | 1 | | |
| 4а | Изображена пирамида по условию задачи. Указана точка В - проекция вершины пирамиды 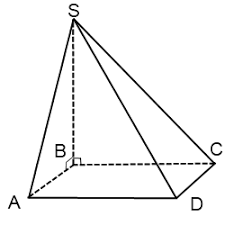 | 1 | |
| 4b | Изображена диагональ прямоугольника   | 1 | |
| Диагональ прямоугольника вычисляется по теореме Пифагора 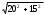 | 1 | | |
| Диагональ прямоугольника равна 25м | 1 | | |
| Указано соотношение катетов в прямоугольном треугольнике с углом в 45° | 1 | Принимается альтернативное решение | |
| Высота пирамиды равна 25м | 1 | | |
| Итого: | 20 | | |