Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4614
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
2 ВАРИАНТ
| Разбаловка заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 1 | 4 | 9 | 6 |
| итого | 20 баллов | |||
1 ... 39 40 41 42 43 44 45 46 ... 59
1. Определите вид многогранника, изображенного на рисунке:
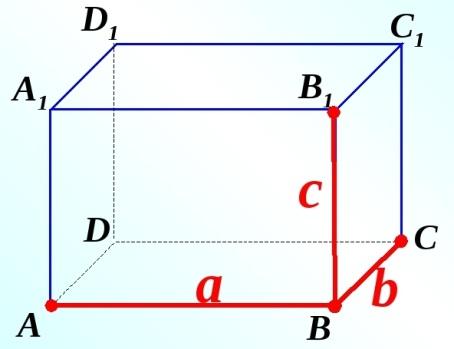
А) прямоугольный параллелепипед;
В) прямой параллелепипед;
С) правильная четырёхугольная призма;
D) параллелепипед.
2. а) Изобразите правильную четырехугольную призму. Изобразите диагональ призмы.
b) Высота призмы равна 8 см, а диагональ основания равна 6см. Найдите диагональ призмы.
3. В прямом параллелепипеде стороны основания равны 6см и 8см, а один из углов основания равен 120°. Высота призмы равна 10
 см. Выполните рисунок по условию задачи.
см. Выполните рисунок по условию задачи.а) Найдите меньшую диагональ параллелепипеда .
b) Вычислите площадь полной поверхности параллелепипеда.
4. Во время строительства пирамидального здания была собрана конструкция с учётом того, что две его равные стены должны быть перпендикулярны основанию здания, а третья стена наклонена к ней под углом 45°.
а) Изобразите конструкцию. Укажите на изображении точку, в которую проектируется вершина пирамиды.
b) Стороны основания пирамиды равны 25 м, 25 м и 30 м. Найдите высоту пирамиды.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | А | 1 | |
| 2а | 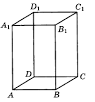 | 1 | |
 | 1 | Принимается альтернативное решение | |
| 2b | Длина диагонали призмы вычисляется по теореме Пифагора 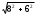 | 1 | |
| 10 см | 1 | | |
| 3а | Выполнен рисунок по условию задачи. | 1 | |
| Указано, что основанием параллелепипеда является параллелограмм. | 1 | | |
| Найден второй угол параллелограмма 60° | 1 | | |
| Длина меньшей диагонали параллелограмма вычисляется по теореме косинусов 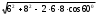 | 1 | | |
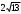 см см | 1 | | |
| Длина меньшей диагонали параллелепипеда вычисляется по теореме Пифагора 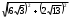 | 1 | | |
| 4 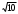 см см | 1 | | |
| 3b | 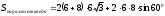 | 1 | |
| 216  см² см² | 1 | | |
| 4а | Изображена пирамида по условию задачи. Указана точка А - проекция вершины пирамиды  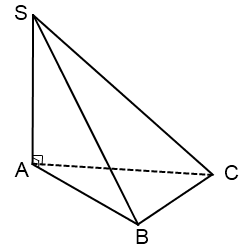 | 1 | Принимается другое обозначение вершин пирамиды |
| 4b | Изображены высота основания пирамиды и высота боковой грани пирамиды  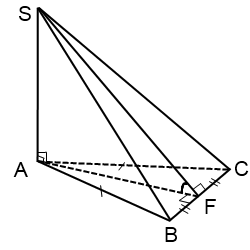 | 1 | Принимается другое обозначение высот |
| Высота основания пирамиды вычисляется по теореме Пифагора 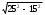 | 1 | | |
| Высота основания пирамиды равна 20м | 1 | | |
| Указано соотношение катетов в прямоугольном треугольнике с углом в 45° | 1 | Принимается альтернативное решение | |
| Высота пирамиды равна 20м | 1 | | |
| Итого: | 20 | | |
3 ВАРИАНТ
| Разбаловка заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 1 | 4 | 9 | 6 |
| итого | 20 баллов | |||
1 ... 40 41 42 43 44 45 46 47 ... 59
1. Определите вид многогранника, изображенного на рисунке:
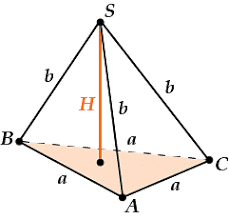
А) треугольная пирамида;
В) правильная четырёхугольная пирамида;
С) правильная треугольная пирамида;
D) четырёхугольная пирамида.
2. а) Изобразите правильную треугольную призму. Изобразите диагональ боковой грани призмы.
b) Диагональ боковой грани призмы равна 13 см, а сторона основания равна 5см. Найдите высоту призмы.
3. В прямом параллелепипеде стороны основания равны 3см и 5см, а один из углов основания равен 60°. Высота призмы равна 5
 см. Выполните рисунок по условию задачи.
см. Выполните рисунок по условию задачи.а) Найдите большую диагональ параллелепипеда .
b) Вычислите площадь полной поверхности параллелепипеда.
4. Во время строительства пирамидального здания была собрана конструкция с учётом того, что две его стены должны быть перпендикулярны прямоугольному основанию здания.
а) Изобразите конструкцию. Укажите на изображении точку, в которую проектируется вершина пирамиды.
b) Стороны основания пирамиды равны 16 м и 12 м. Боковое ребро пирамиды, противоположное её прямому двугранному углу, наклонено к основанию под углом 45°. Найдите высоту пирамиды.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | С | 1 | |
| 2а |  | 1 | |
 | 1 | Принимается альтернативное решение | |
| 2b | Длина высоты призмы вычисляется по теореме Пифагора 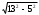 | 1 | |
| 12 см | 1 | | |
| 3а | Выполнен рисунок по условию задачи. | 1 | |
| Указано, что основанием параллелепипеда является параллелограмм. | 1 | | |
| Найден второй угол параллелограмма 120° | 1 | | |
| Длина большей диагонали параллелограмма вычисляется по теореме косинусов 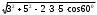 | 1 | | |
| 7см | 1 | | |
| Длина большей диагонали параллелепипеда вычисляется по теореме Пифагора 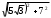 | 1 | | |
| 2 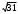 см см | 1 | | |
| 3b | 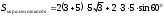 | 1 | |
| 95  см² см² | 1 | | |
| 4а | Изображена пирамида по условию задачи. Указана точка В - проекция вершины пирамиды   | 1 | |
| 4b | Изображена диагональ прямоугольника    | 1 | |
| Диагональ прямоугольника вычисляется по теореме Пифагора 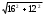 | 1 | | |
| Диагональ прямоугольника равна 20м | 1 | | |
| Указано соотношение катетов в прямоугольном треугольнике с углом в 45° | 1 | Принимается альтернативное решение | |
| Высота пирамиды равна 20м | 1 | | |
| Итого: | 20 | | |
4 ВАРИАНТ
| Разбаловка заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 1 | 4 | 9 | 6 |
| итого | 20 баллов | |||
1 ... 41 42 43 44 45 46 47 48 ... 59