Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4600
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
ЗАДАНИЯ
| Оценивание заданий работы | |||||
| № задания | 1 | 2 | 3 | 4 | 5 |
| Количество баллов | 4 | 4 | 3 | 3 | 3 |
| Всего баллов | 17 баллов | ||||
1 ВАРИАНТ
1. Вычислите: а)
-
Упростите выражение:
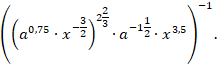
-
Избавьтесь от знака корня в знаменателе дроби:
4. а) Постройте график функции:
b) Используя построенный график функции, постройте график функции
5. Вычислите интеграл:
2 ВАРИАНТ
1. Вычислите: а)
-
Упростите выражение:
3. Избавьтесь от знака корня в знаменателе дроби:
4. а) Постройте график функции:
b) Используя построенный график функции, постройте график функции
5. Вычислите интеграл:
3 ВАРИАНТ
1. Вычислите: а)
-
Упростите выражение:
3. Избавьтесь от знака корня в знаменателе дроби:
4. а) Постройте график функции:
b) Используя построенный график функции, постройте график функции
5. Вычислите интеграл:
4 ВАРИАНТ
1. Вычислите: а)
-
Упростите выражение:
3. Избавьтесь от знака корня в знаменателе дроби:
4. а) Постройте график функции:
b) Используя построенный график функции, постройте график функции
5. Вычислите интеграл:
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Использует свойства корня n-ой степени для нахождения значения выражений | 1a | применяет свойство корня n-ой степени; | 1 |
| вычисляет значение выражения; | 1 | ||
| 1b | применяет свойство корня n-ой степени; | 1 | |
| вычисляет значение выражения; | 1 | ||
| Применяет свойства степени с рациональным показателем для упрощения выражения | 2 | Применяет свойство возведения произведения в степень; | 1 |
| Применяет свойство возведения степени в степень; | 1 | ||
| Применяет свойство произведения степеней с одинаковым основанием; | 1 | ||
| упрощает выражение; | 1 | ||
| Использует свойство корня n-ой степени для преобразования иррациональных выражений | 3 | выполняет преобразования; | 1 |
| использует формулы сокращенного умножения для выражений с рациональным показателем в знаменателе; | 1 | ||
| записывает итоговое выражение; | 1 | ||
| Строит график степенной функции с действительным показателем в зависимости от показателя степени | 4a | Строит график заданной степенной функции; | 1 |
| 4b | Применяет параллельный перенос графика; | 1 | |
| строит график заданной функции; | 1 | ||
| Использует правило нахождения интеграла степенной функции с действительным показателем | 5 | Применяет свойства корня n-ой степени; | 1 |
| применяет правила первообразных; | 1 | ||
| Находит неопределенный интеграл степенной функции. | 1 | ||
| Итого: | 17 | ||
- 1 2 3 4 5 6 7 8 9 ... 59
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»


ФИ УЧАЩЕГОСЯ ________________________________________
| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Использует свойства корня n-ой степени для нахождения значения выражений | Затрудняется в записи свойств корня п-ой степени для нахождения значения выражений | Допускает ошибки в использованиия свойство корня n-ой степени для нахождения значения выражений | Находит значения выражений, используя свойства корня n-ой степени |
| Применяет свойства степени с рациональным показателем для преобразования выражения | Затрудняется в применении свойств степени с рациональным показателем для преобразования алгебраических выражений | Применяет свойства степени с рациональным показателем, но допускает ошибки в дальнейших алгебраических преобразованиях | Упрощает выражение, применяя свойства степени с рациональным показателем |
| Использует свойство корня n- ой степени для преобразования иррациональных выражений | Затрудняется в применении свойств степени с рациональным показателем для преобразования алгебраических выражений | Применяет свойства степени с рациональным показателем, но допускает ошибки в дальнейших алгебраических преобразованиях | Избавляется от иррациональности в знаменателе |
| Строит график степенной функции с действительным показателем в зависимости от показателя степени | Затрудняется в построении графиков степенных функций. | Допускает погрешности при построении графиков степенных функций | Строит графики степенных функций |
| Использует правило нахождения интеграла степенной функции с действительным показателем | Затрудняется в применении правил нахождения интеграла степенной функции с действительным показателем | Допускает ошибки в применении правил нахождения интеграла степенной функции с действительным показателем | Вычисляет интеграл степенной функции с действительным показателем |
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ
«ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
| Тема | Иррациональные уравнения и их системы. Иррациональные неравенства |
| Цель обучения | 1.2.2.1 Знать определение иррационального уравнения, уметь определять его область допустимых значений 11.2.2.2 Уметь решать иррациональные уравнения методом возведения обеих частей уравнения в n-ю степень 11.2.2.3 Уметь решать иррациональные уравнения методом замена переменной 11.2.2.5 Уметь решать иррациональные неравенства |
| Критерий оценивания | Обучающийся Определяет область допустимых значений иррационального уравнения Решает иррациональное уравнение методом возведения обеих частей уравнения в n-ую степень Решает иррациональное уравнение методом замены переменной Решает иррациональное неравенство |
| Уровень мыслительных навыков | Применение Навыки высокого порядка |
| Время выполнения | 30 минут |
ЗАДАНИЯ
| Оценивание заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 2 | 4 | 7 | 4 |
| Всего баллов | 19 баллов | |||
-
ВАРИАНТ
-
Не решая уравнение, покажите, что уравнение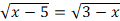
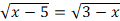 не имеет решений.
не имеет решений. -
Решите уравнение: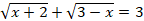
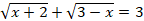
-
Дано уравнение: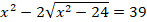
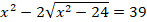
-
Используя метод замены переменной, приведите данное уравнение к виду:
-
t2 − 2t − 15 = 0 .
-
Покажите, что решением уравнения будут корени: x =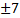
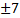
-
Решите неравенство: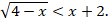
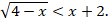
-
ВАРИАНТ
-
Не решая уравнение, покажите, что уравнение

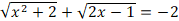
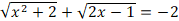 не имеет решений.
не имеет решений.
-
Решите уравнение: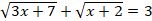
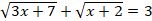
-
Дано уравнение: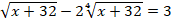
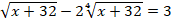
-
Используя метод замены переменной, приведите данное уравнение к виду:
-
t2 − 2t − 3 = 0 .
-
Покажите, что решением уравнения будет корень: x =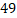
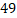
Решите неравенство:
3 ВАРИАНТ
-
Не решая уравнение, покажите, что уравнение

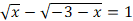
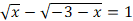 не имеет решений.
не имеет решений. -
Решите уравнение: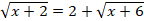
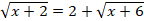
-
Дано уравнение: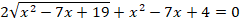
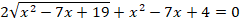
-
Используя метод замены переменной, приведите данное уравнение к виду:
-
t2 + 2t − 15 = 0.
-
Покажите, что решением уравнения будут корени: x = 2;5.
-
Решите неравенство: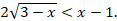
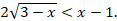
-
ВАРИАНТ
-
Не решая уравнение, покажите, что уравнение

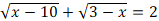
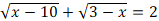 не имеет решений.
не имеет решений. -
Решите уравнение: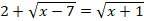
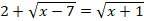
-
Дано уравнение: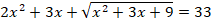
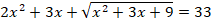
-
Используя метод замены переменной, приведите данное уравнение к виду:
-
t2 + t − 42 = 0.
-
Покажите, что решением уравнения будут корни: x =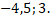
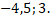
-
Решите неравенство: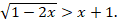
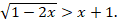
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Определяет область допустимых значений иррационального уравнения | 1 | Определяет область допустимых значений; | 1 |
| делает вывод о том, что уравнение не имеет решений; | 1 | ||
| Решает иррациональное уравнение методом возведения обеих частей уравнения в n-ую степень | 2 | находит область допустимых значений; | 1 |
| возводит обе части уравнения в квадрат, выполнив предварительные преобразования; | 1 | ||
| возводит повторно обе части уравнения в квадрат; | 1 | ||
| Находит искомое значение, решая полученное уравнение и учитывая область допустимых значений; | 1 | ||
| Решает иррациональное уравнение методом замены переменной | 3a | Определяет область допустимых значений; | 1 |
| вводит новую переменную; | 1 | ||
| приводит к квадратному уравнению; | 1 | ||
| 3b | решает уравнение относительно новой переменной; | 1 | |
| находит корни квадратного уравнения; | 1 | ||
| возвращается к замене переменной; | 1 | ||
| Находит корни данного уравнения с учетом области допустимых значений; | 1 | ||
| Решает иррациональное неравенство | 4 | составляет равносильную систему; | 1 |
| решает первое неравенство; | 1 | ||
| решает второе неравенство; | 1 | ||
| находит общее решение неравенства. | 1 | ||
| Итого: | 19 | ||