ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 369
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1. Основные цели и задачи прикладного корреляционно-регрессионного анализа
2.2. Постановка задачи регрессии
2.4. Коэффициент корреляции, коэффициент детерминации, корреляционное отношение
3. Классическая линейная модель множественной регрессии
3.2. Оценивание коэффициентов КЛММР
X1 (тонн) и расстоянием X2(тыс.км) по 20 транспортным компаниям. Исходные данные приведены в таблице 3.1.
В данном примере мы располагаем пространственной выборкой объема n=20, число объясняющих переменных k=2.
Модель специфицируем в виде линейной функции:
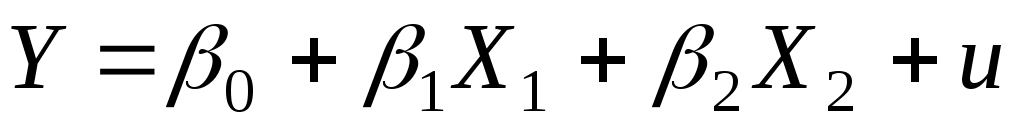. (3.9)
Следовательно, система нормальных уравнений для модели (3.9) будет иметь вид
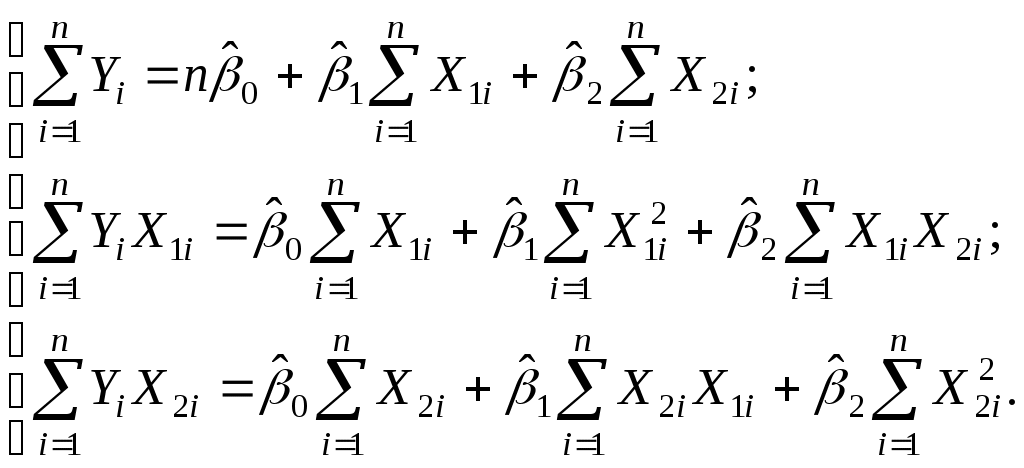(3.10)
Рассчитаем по данным табл. 3.1 необходимые для составления указанной системы суммы:
Получим систему нормальных уравнений (3.10) в виде:
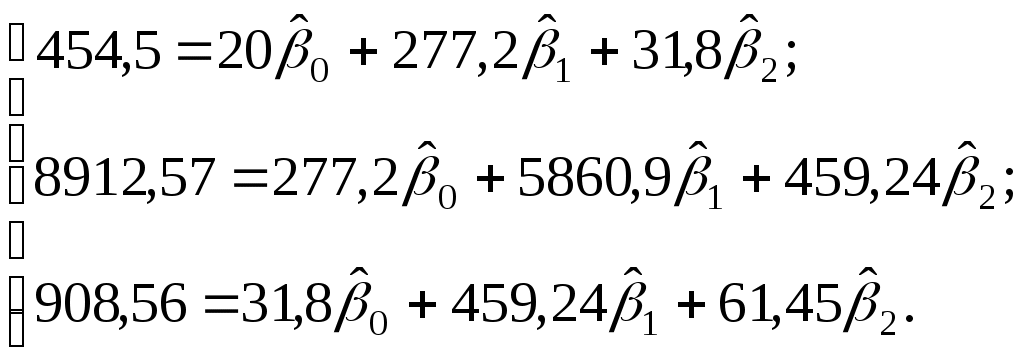
Решая последнюю систему линейных алгебраических уравнений, например методом Крамера, получим:
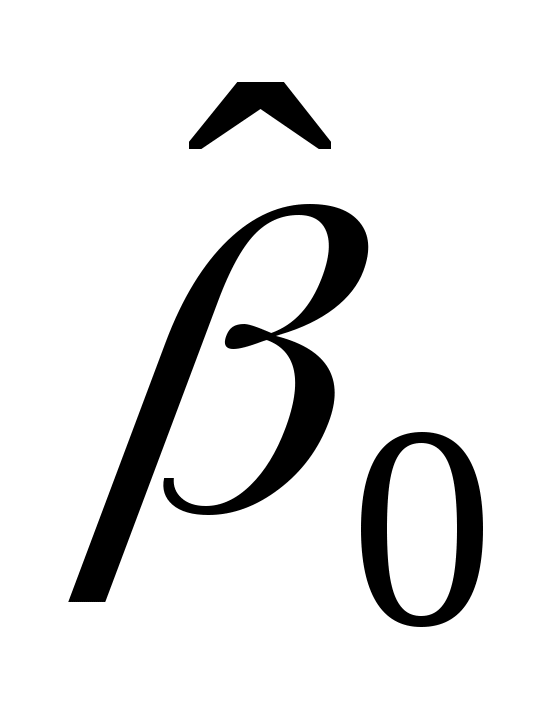=-17,31; 
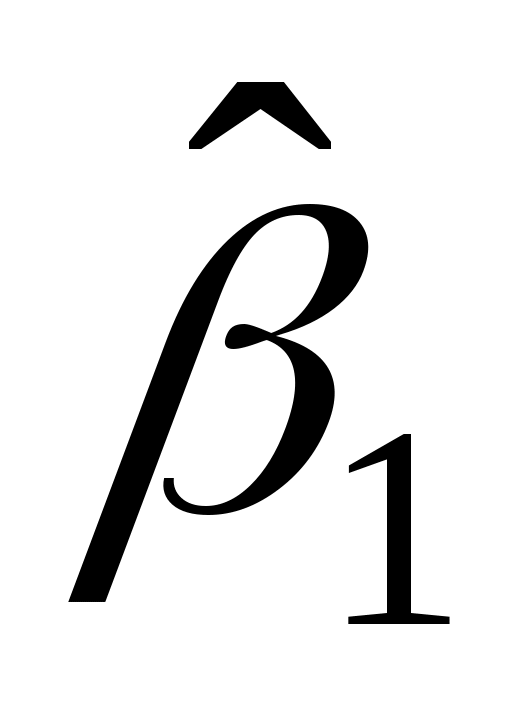=1,16; 
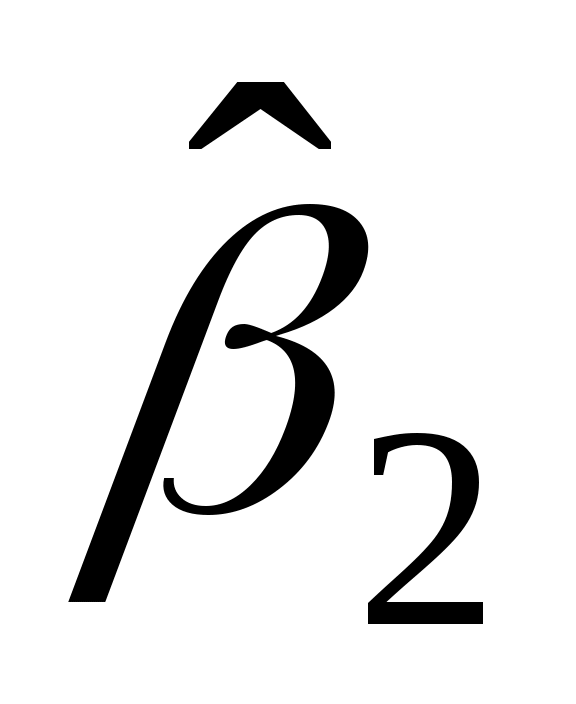=15,10.
Уравнение регрессии имеет вид:
Y=-17,31+1,16X1+15,10X2.
Или, с учетом (3.8) и расчетов:
=
=
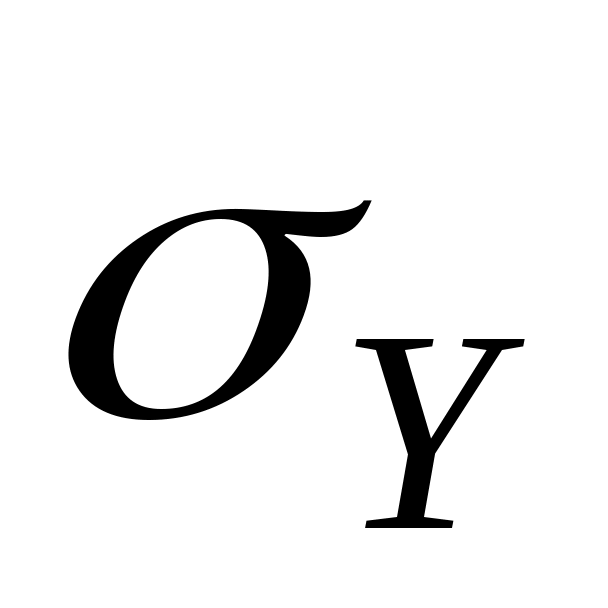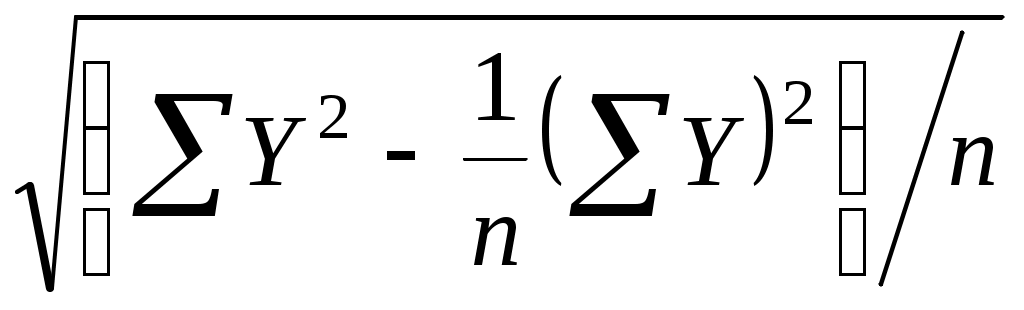=19,85,
=
=
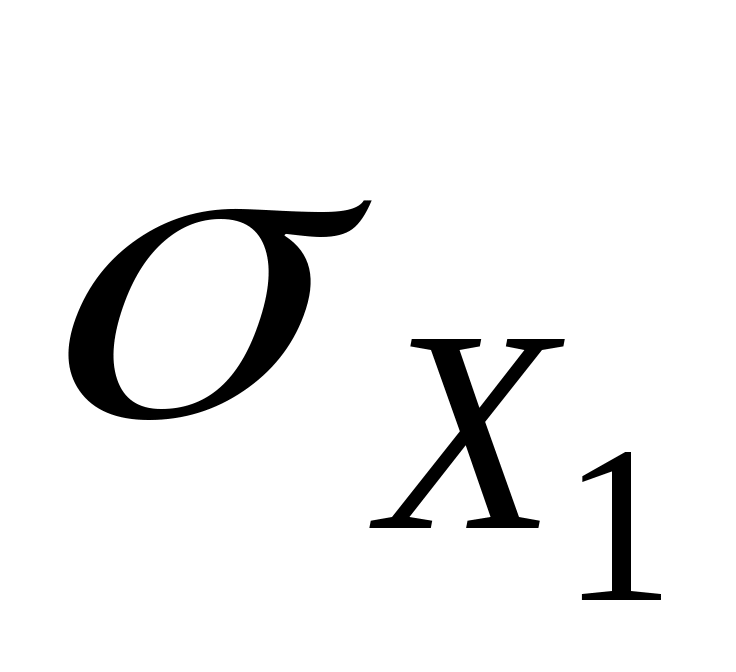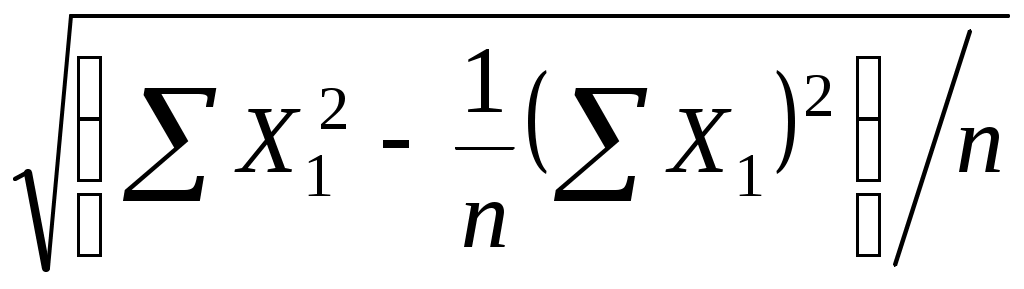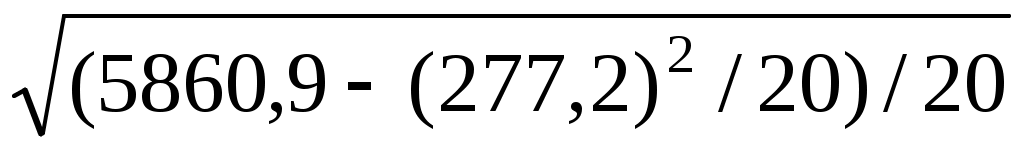=10,05,
=
=
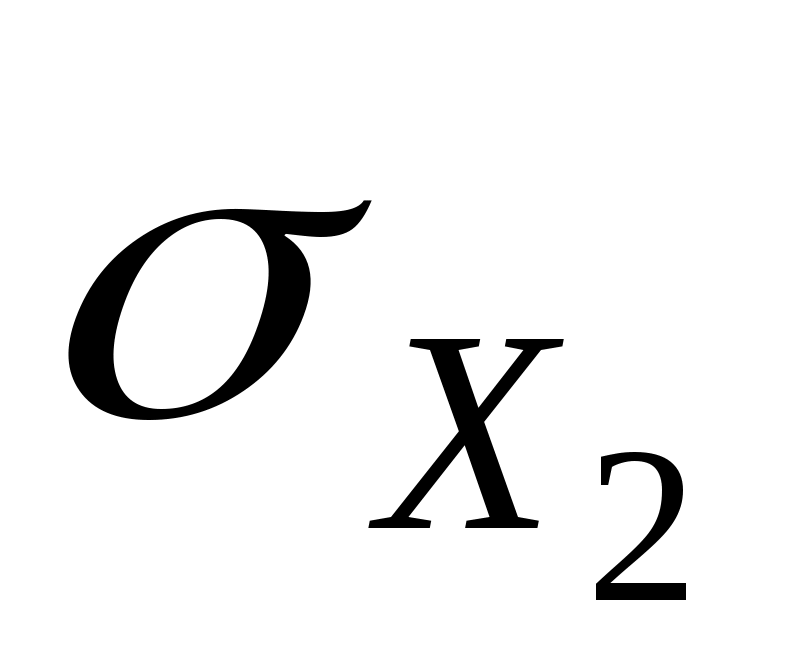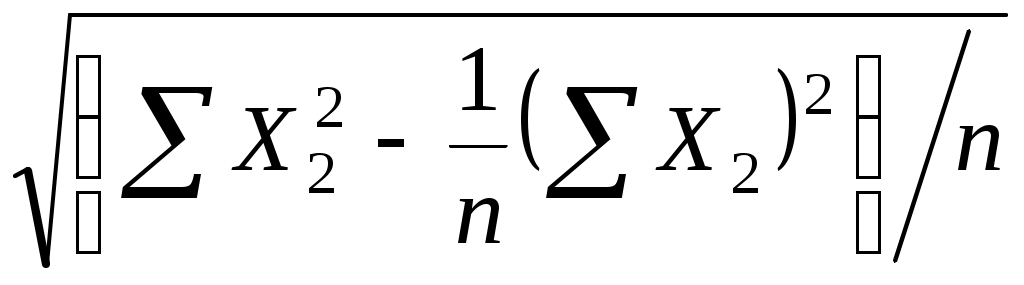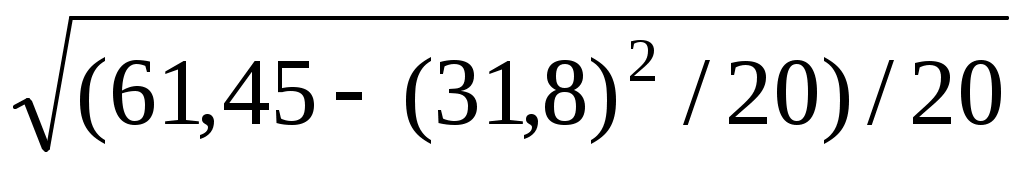=0,74.
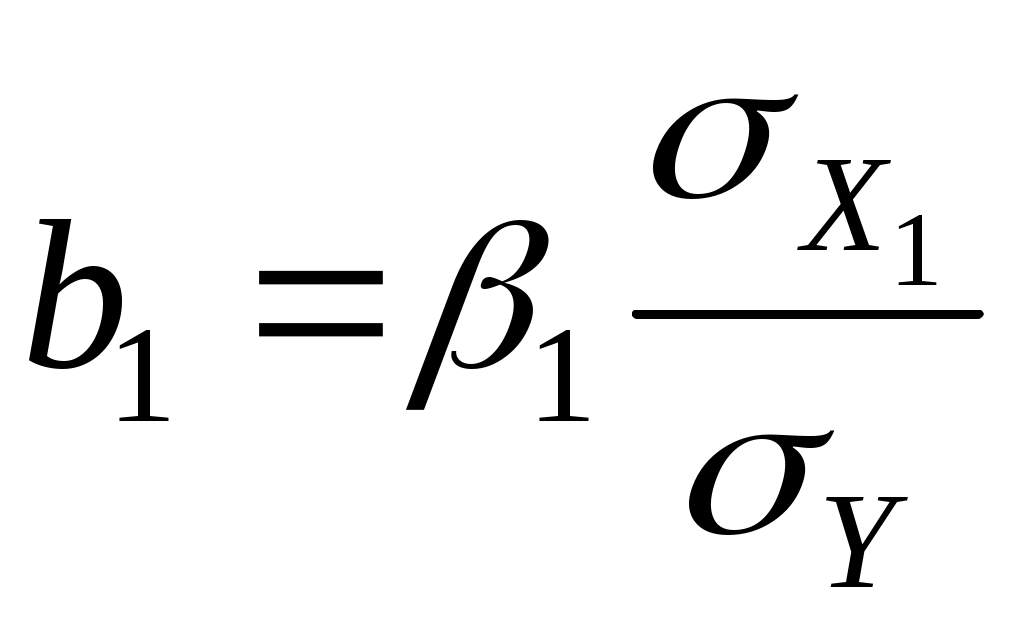=1,16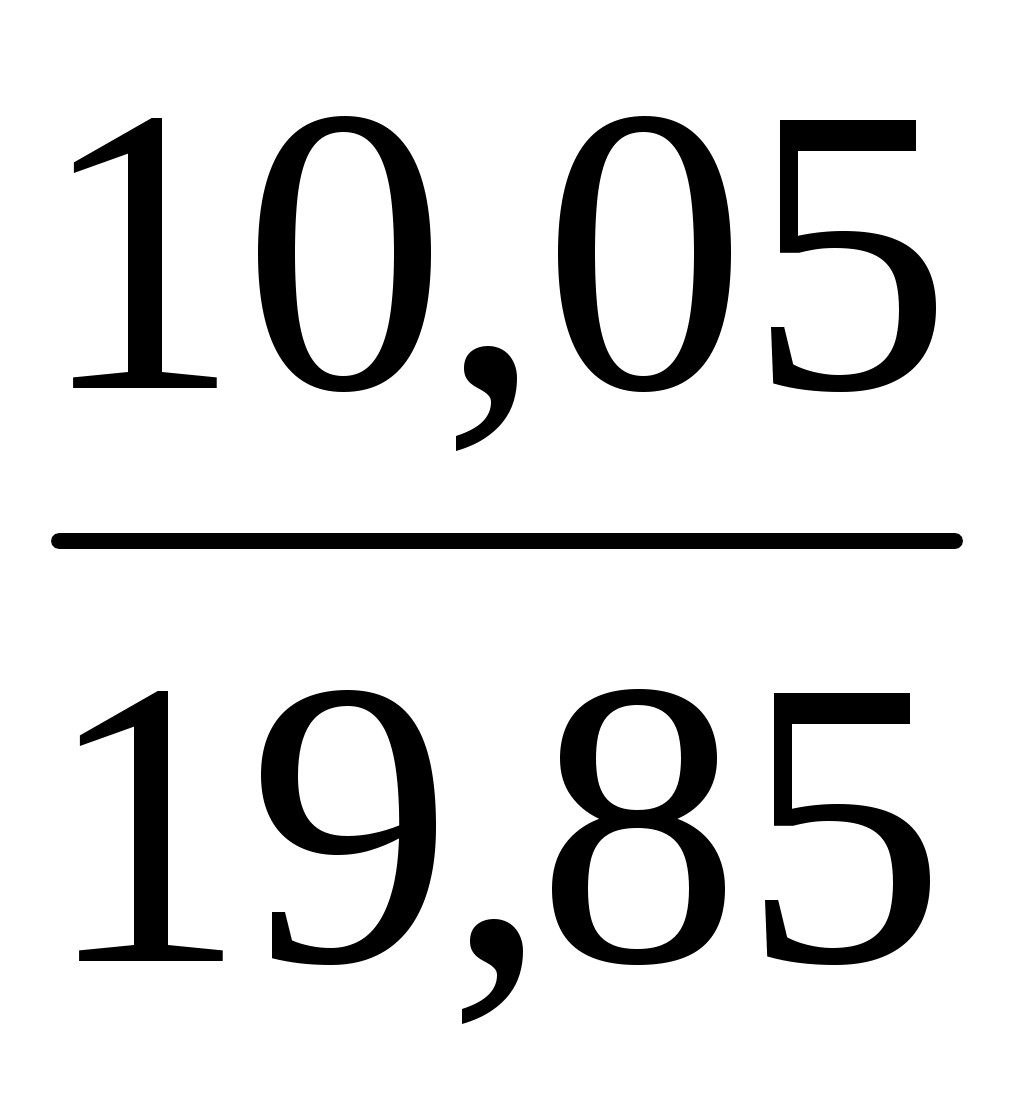
=0,77, 
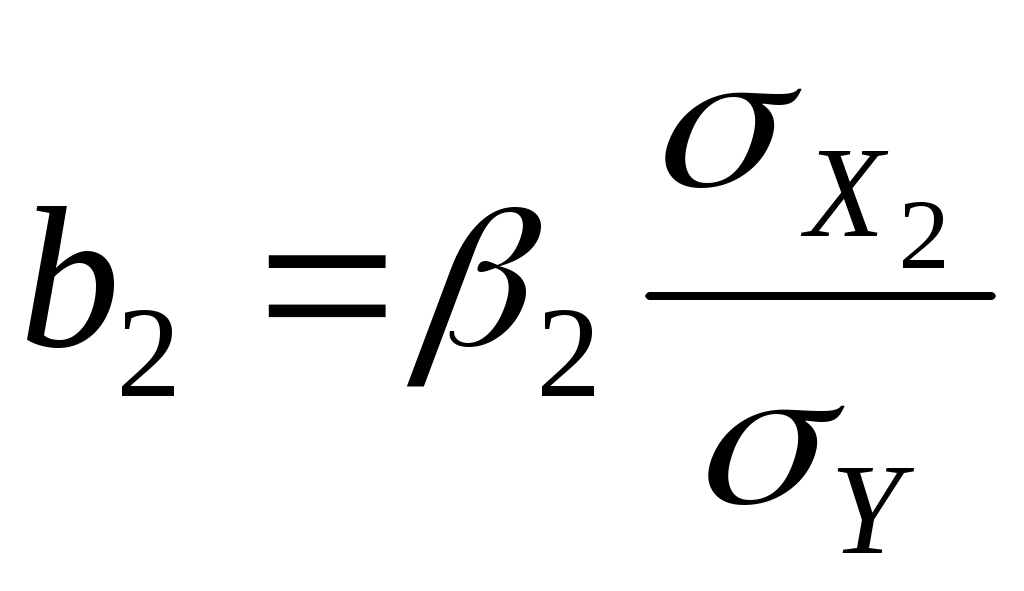=15,10
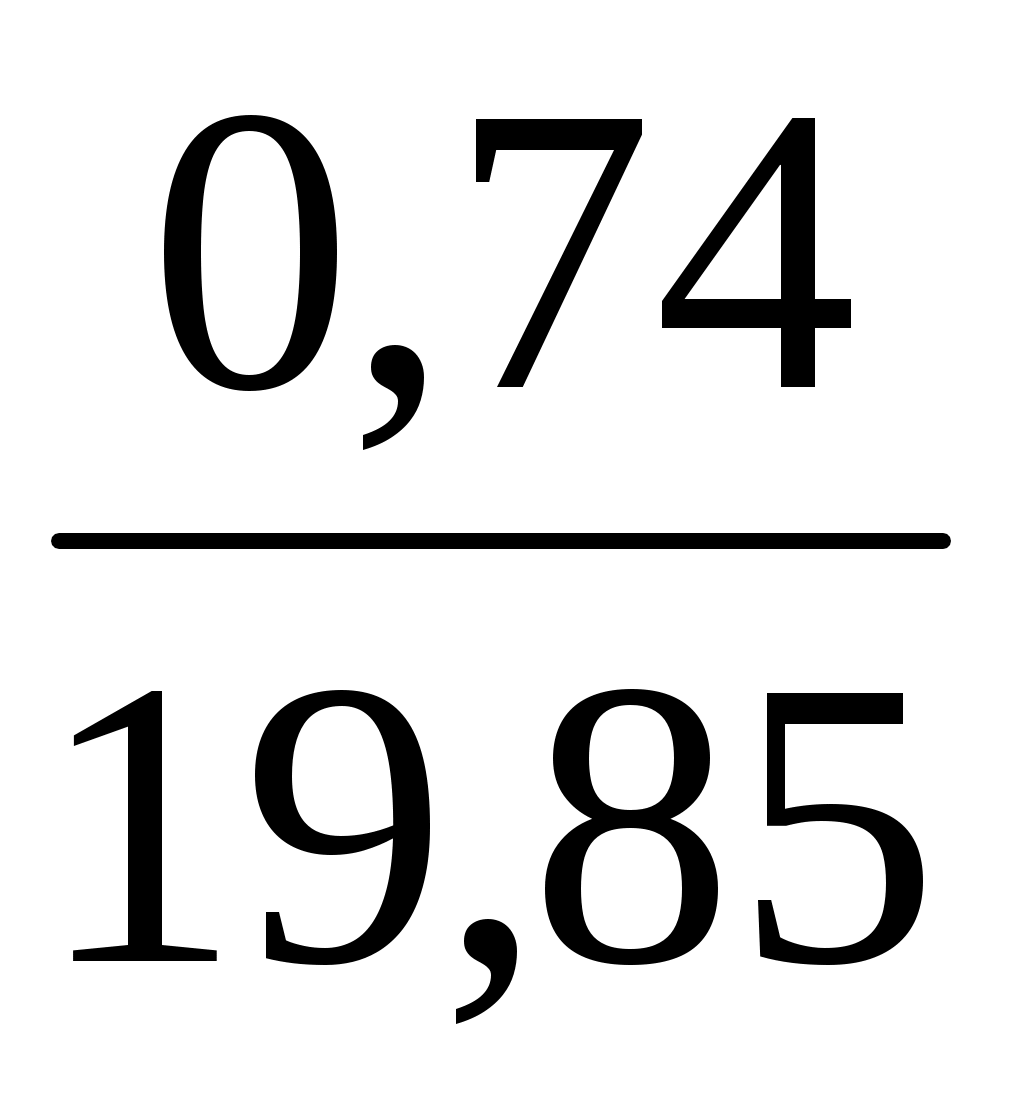=0,56
уравнение регрессии в стандартизованном масштабе:
.
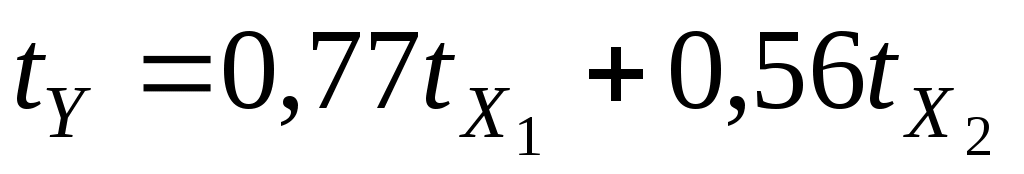То есть с ростом веса груза на одну сигму при неизменном расстоянии стоимость грузовых автомобильных перевозок увеличивается в среднем на 0,77 сигмы. Поскольку 0,77>0,56, то влияние веса груза на стоимость грузовых автомобильных перевозок больше, чем фактора расстояния.
Рассчитаем коэффициенты эластичности
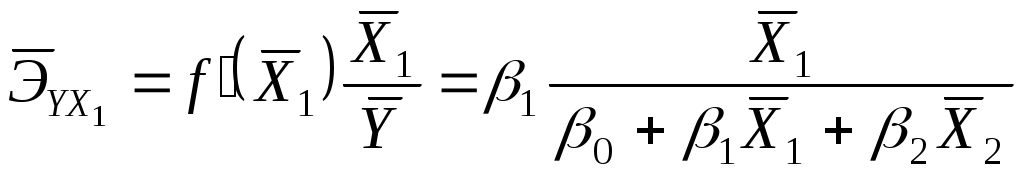
= 1,1613,86/(-17,31 + 1,1613,86 + 15,101,59) = 0,71,
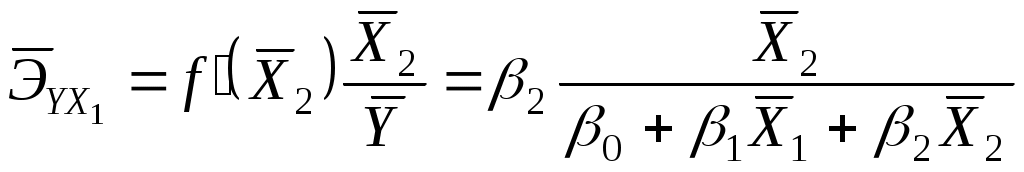= 1,05.
С увеличением среднего веса груза на 1% от его среднего уровня средняя стоимость перевозок возрастет на 0,71% от своего среднего уровня, при увеличении среднего расстояния перевозок на 1% средняя стоимость доставки груза увеличится на 1,05%. Различия в силе влияния факторов на результат полученные при сравнении уравнения регрессии в стандартизованном масштабе и коэффициентов эластичности объясняются тем, что коэффициент эластичности рассчитывается исходя из соотношения средних, а стандартизованные коэффициенты регрессии из соотношения средних квадратических отклонений.
Поскольку обычно статистики используют показатель грузооборота, вычисляемый как сумма произведений массы перевезенных грузов на расстояние перевозки, то построим регрессию стоимости 1 км грузовых автомобильных перевозок Y на грузооборот Q (Q=X1X2):
P = 5,88 + 0,48Q 0,003Q2,
причем регрессор Q2 = Q*Q включен исходя из соображений известного экономического закона убывающей предельной полезности, согласно которому в данном случае стоимость перевозки на 1 км должна уменьшаться с ростом грузооборота, т.е. коэффициент при Q2 должен иметь (и в построенном уравнении имеет) отрицательный знак.
Как уже говорилось в разделе 2.3, регрессионные модели не ограничиваются классом линейных функций. Линеаризация нелинейных функций в уравнении регрессии имеет особенности, рассмотренные в примере.
Пример 2. Исследуется зависимость между выпуском Q(млн. $) и затратами труда L (чел.) и капитала K (млн. $) в металлургической промышленности по 27 американским компаниям. Исходные данные приведены в таблице 3.2.
Таблица 3.2
Мы располагаем пространственной выборкой объема n=27, число объясняющих переменных k=2.
Модель зависимости между выпуском и затратами труда и капитала, как правило, специфицируется в виде производственной функции, чаще всего Кобба-Дугласа:
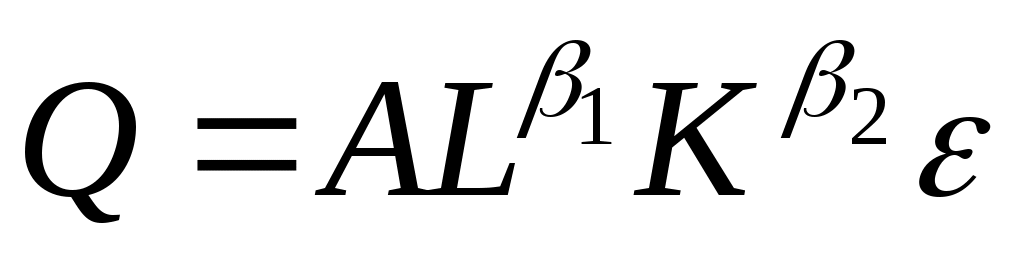. (3.11)
Поскольку модель (3.11) является нелинейной, преобразуем ее к виду линейной по параметрам. Для этого возьмем логарифм от обеих частей в уравнении (3.11):
.
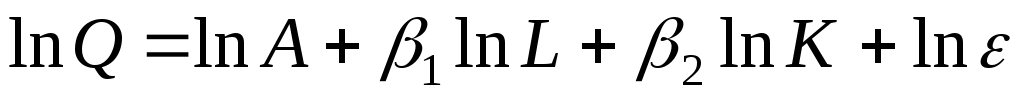Переобозначим для удобства Y=lnQ, 0=lnA,X1=lnL, X2=lnK, u=ln, тогда имеем линейную модель вида:
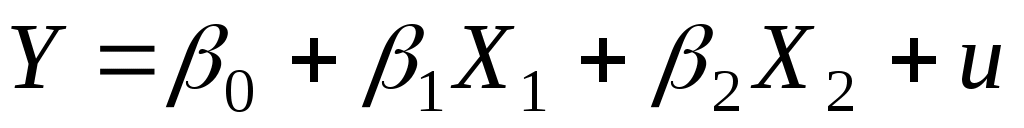. (3.12)
Исходные данные к модели вида (3.11) получаются логарифмированием чисел, представленных в таблице 3.2. Соответственно получим табл. 3.3.
После процедуры лианеризации система нормальных уравнений для модели (3.11) будет иметь такой же вид, как и система (3.10)
Рассчитаем по данным табл. 3.3 необходимые для составления указанной системы суммы:
Получим систему нормальных уравнений после подстановки соответствующих значений в (3.10) в виде:
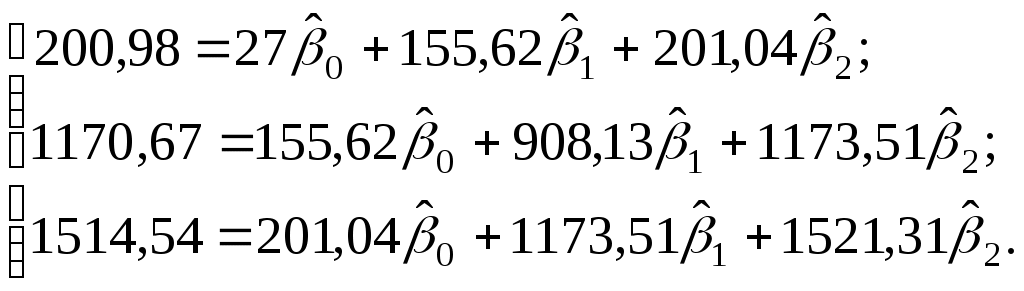
Решая последнюю систему методом Крамера, получим:
=1,11, 
=0,56, 
=0,41.
Уравнение регрессии имеет вид:
Y=1,11+0,56X1+0,41X2.
Или, с учетом (3.8) и расчетов:
=0,75, 
=0,65, 
=0,96, 
=0,56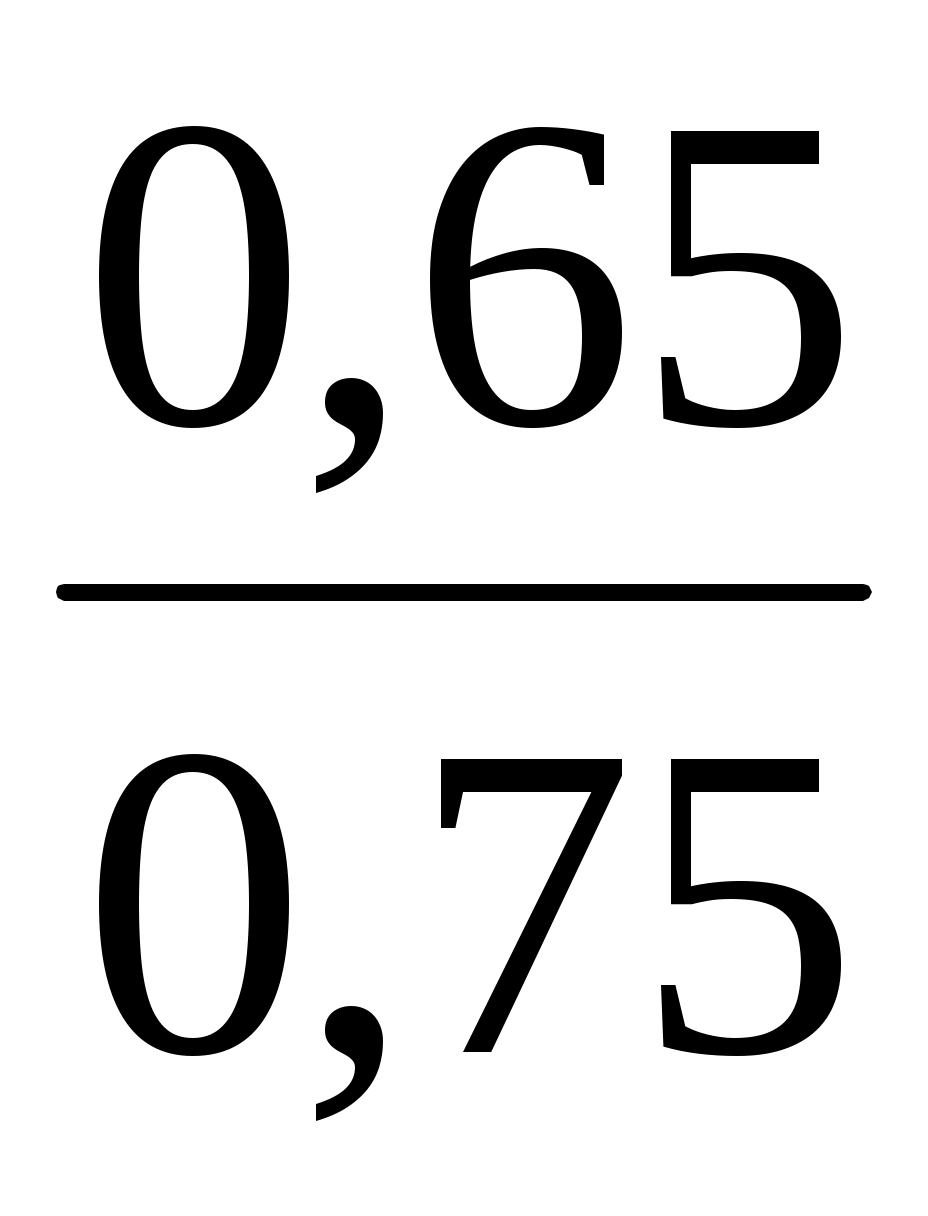
=0,48, 
=0,41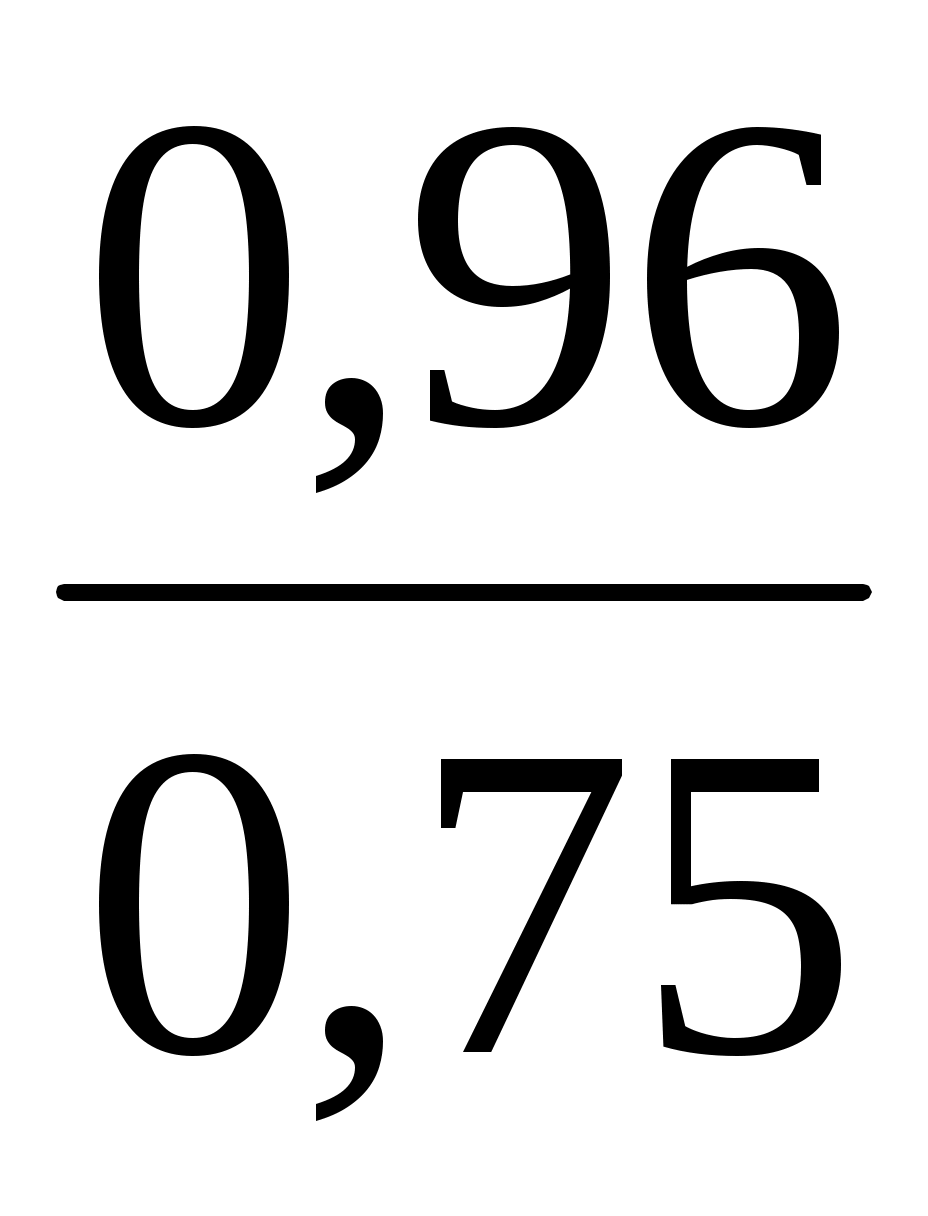
=0,52 уравнение регрессии в стандартизованном масштабе:
.
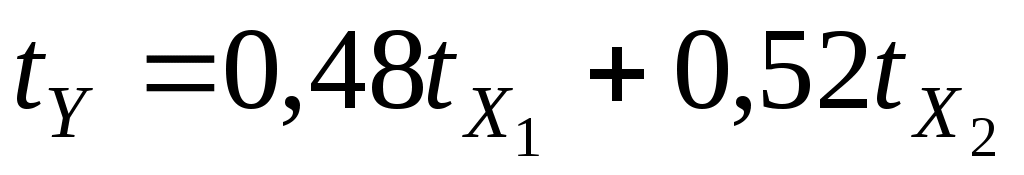Нетрудно восстановить (учитывая, что A=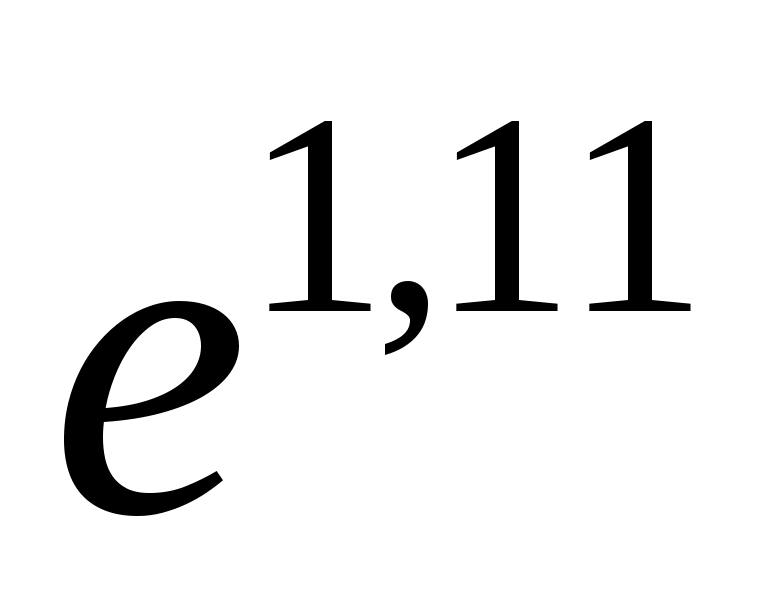
=3,03) исходную модель (3.9)
.
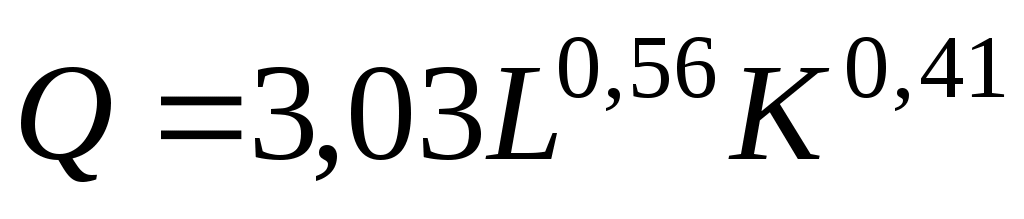Эластичность выпуска продукции Q по труду L равна 0,56, а эластичность выпуска продукции Q по капиталу K равна 0,41. Следовательно увеличение затрат труда на 1% приведет к росту выпуска продукции на 0,56%, а увеличение затрат капитала на 1% приведет к росту выпуска продукции на 0,41%.
Очевидно, что обе величины и должны находиться между нулем и единицей. Они должны быть положительными, так как увеличение затрат факторов должно вызывать рост выпуска. В то же время, вероятно, они будут меньше единицы, т.к. мы предполагаем, что уменьшение эффекта от масштаба производства приводит к более медленному росту выпуска продукции, чем затрат производственных факторов, если другие факторы остаются постоянными.
Таблица 3.1
| Y | 51 | 16 | 74 | 7,5 | 33,0 | 26,0 | 11,5 | 52 | 15,8 | 8,0 | 26 | 6,0 | 5,8 | 13,8 | 6,20 | 7,9 | 5,4 | 56,0 | 25,5 | 7,1 |
| X1 | 35 | 16 | 18 | 2,0 | 14,0 | 33,0 | 20 | 25 | 13 | 2,0 | 21 | 11,0 | 3 | 3,5 | 2,80 | 17,0 | 3,4 | 24,0 | 9,0 | 4,5 |
| X2 | 2 | 1,1 | 2,55 | 1,7 | 2,4 | 1,55 | 0,6 | 2,3 | 1,4 | 2,1 | 1,3 | 0,35 | 1,65 | 2,9 | 0,75 | 0,6 | 0,9 | 2,5 | 2,2 | 0,95 |
В данном примере мы располагаем пространственной выборкой объема n=20, число объясняющих переменных k=2.
Модель специфицируем в виде линейной функции:
. (3.9)Следовательно, система нормальных уравнений для модели (3.9) будет иметь вид
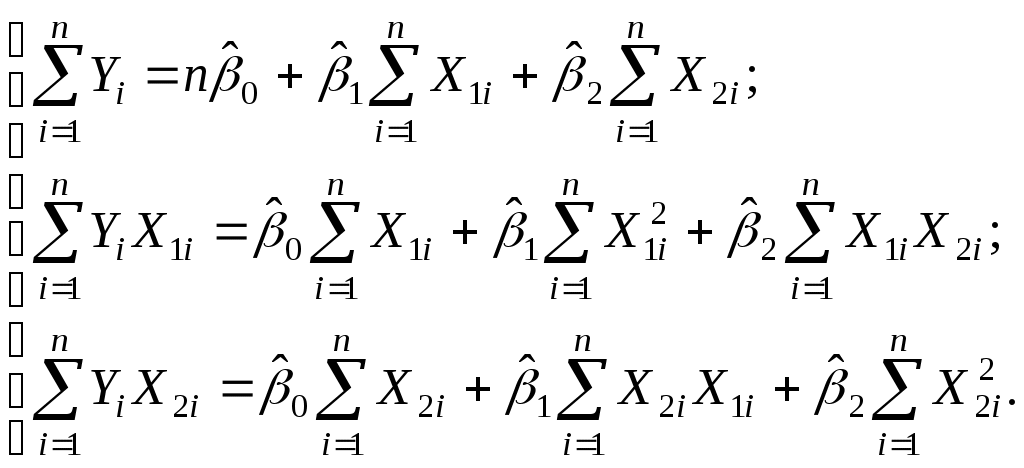(3.10)Рассчитаем по данным табл. 3.1 необходимые для составления указанной системы суммы:
| Y=454,5; | X1=277,2; | X2=31,8; |
| Y2=18206,89; |  =5860,9; |  =61,45; |
 =22,73; |  =13,86; |  =1,59; |
| X1Y=8912,57; | X2Y=908,56; | X1X2=459,24; |
Получим систему нормальных уравнений (3.10) в виде:
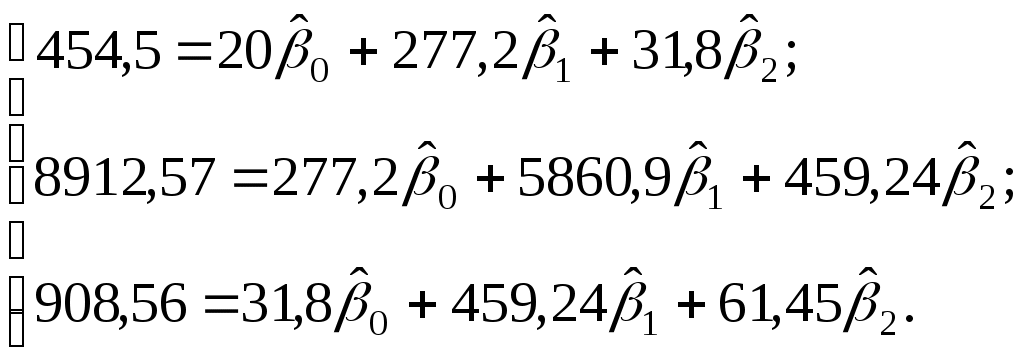
Решая последнюю систему линейных алгебраических уравнений, например методом Крамера, получим:
=-17,31; =1,16; =15,10.Уравнение регрессии имеет вид:
Y=-17,31+1,16X1+15,10X2.
Или, с учетом (3.8) и расчетов:
= = =19,85, = = =10,05, = = =0,74. =1,16 =0,77, =15,10 =0,56уравнение регрессии в стандартизованном масштабе:
.То есть с ростом веса груза на одну сигму при неизменном расстоянии стоимость грузовых автомобильных перевозок увеличивается в среднем на 0,77 сигмы. Поскольку 0,77>0,56, то влияние веса груза на стоимость грузовых автомобильных перевозок больше, чем фактора расстояния.
Рассчитаем коэффициенты эластичности
= 1,1613,86/(-17,31 + 1,1613,86 + 15,101,59) = 0,71,
= 1,05. С увеличением среднего веса груза на 1% от его среднего уровня средняя стоимость перевозок возрастет на 0,71% от своего среднего уровня, при увеличении среднего расстояния перевозок на 1% средняя стоимость доставки груза увеличится на 1,05%. Различия в силе влияния факторов на результат полученные при сравнении уравнения регрессии в стандартизованном масштабе и коэффициентов эластичности объясняются тем, что коэффициент эластичности рассчитывается исходя из соотношения средних, а стандартизованные коэффициенты регрессии из соотношения средних квадратических отклонений.
Поскольку обычно статистики используют показатель грузооборота, вычисляемый как сумма произведений массы перевезенных грузов на расстояние перевозки, то построим регрессию стоимости 1 км грузовых автомобильных перевозок Y на грузооборот Q (Q=X1X2):
P = 5,88 + 0,48Q 0,003Q2,
причем регрессор Q2 = Q*Q включен исходя из соображений известного экономического закона убывающей предельной полезности, согласно которому в данном случае стоимость перевозки на 1 км должна уменьшаться с ростом грузооборота, т.е. коэффициент при Q2 должен иметь (и в построенном уравнении имеет) отрицательный знак.
Как уже говорилось в разделе 2.3, регрессионные модели не ограничиваются классом линейных функций. Линеаризация нелинейных функций в уравнении регрессии имеет особенности, рассмотренные в примере.
Пример 2. Исследуется зависимость между выпуском Q(млн. $) и затратами труда L (чел.) и капитала K (млн. $) в металлургической промышленности по 27 американским компаниям. Исходные данные приведены в таблице 3.2.
Таблица 3.2
Q | L | K | | Q | L | K |
| 657,29 | 162,31 | 279,99 | | 1917,55 | 536,73 | 2109,34 |
| 935,93 | 214,43 | 542,50 | | 9849,17 | 1564,83 | 13989,55 |
| 1110,65 | 186,44 | 721,51 | | 1088,27 | 214,62 | 884,24 |
| 1200,89 | 245,83 | 1167,68 | | 8095,63 | 1083,10 | 9119,70 |
| 1052,68 | 211,40 | 811,77 | | 3175,39 | 521,74 | 5686,99 |
| 3406,02 | 690,61 | 4558,02 | | 1653,38 | 304,85 | 1701,06 |
| 2427,89 | 452,79 | 3069,91 | | 5159,31 | 835,69 | 5206,36 |
| 4257,46 | 714,20 | 5585,01 | | 3378,40 | 284,00 | 3288,72 |
| 1625,19 | 320,54 | 1618,75 | | 592,85 | 150,77 | 357,32 |
| 1272,05 | 253,17 | 1562,08 | | 1601,98 | 259,91 | 2031,93 |
| 1004,45 | 236,44 | 662,04 | | 2065,85 | 497,60 | 2492,98 |
| 598,87 | 140,73 | 875,37 | | 2293,87 | 275,20 | 1711,74 |
| 853,10 | 145,04 | 1696,98 | | 745,67 | 137,00 | 768,59 |
| 1165,63 | 240,27 | 1078,79 | | | | |
Мы располагаем пространственной выборкой объема n=27, число объясняющих переменных k=2.
Модель зависимости между выпуском и затратами труда и капитала, как правило, специфицируется в виде производственной функции, чаще всего Кобба-Дугласа:
. (3.11)Поскольку модель (3.11) является нелинейной, преобразуем ее к виду линейной по параметрам. Для этого возьмем логарифм от обеих частей в уравнении (3.11):
.Переобозначим для удобства Y=lnQ, 0=lnA,X1=lnL, X2=lnK, u=ln, тогда имеем линейную модель вида:
. (3.12)Исходные данные к модели вида (3.11) получаются логарифмированием чисел, представленных в таблице 3.2. Соответственно получим табл. 3.3.
После процедуры лианеризации система нормальных уравнений для модели (3.11) будет иметь такой же вид, как и система (3.10)
Рассчитаем по данным табл. 3.3 необходимые для составления указанной системы суммы:
| Y=200,98; | X1=155,62; | X2=201,04; |
| Y2=1511,07; |  =908,13; |  =1521,31; |
| =7,44; |  =5,76; |  =7,45; |
| X1Y=1170,67; | X2Y=1514,54; | X1X2=1173,51; |
Таблица 3.3
Y | X1 | X2 | | Y | X1 | X2 |
| 6,49 | 5,09 | 5,63 | | 7,56 | 6,29 | 7,65 |
| 6,84 | 5,37 | 6,30 | | 9,20 | 7,36 | 9,55 |
| 7,01 | 5,23 | 6,58 | | 6,99 | 5,37 | 6,78 |
| 7,09 | 5,50 | 7,06 | | 9,00 | 6,99 | 9,12 |
| 6,96 | 5,35 | 6,70 | | 8,06 | 6,26 | 8,65 |
| 8,13 | 6,54 | 8,42 | | 7,41 | 5,72 | 7,44 |
| 7,79 | 6,12 | 8,03 | | 8,55 | 6,73 | 8,56 |
| 8,36 | 6,57 | 8,63 | | 8,13 | 5,65 | 8,10 |
| 7,39 | 5,77 | 7,39 | | 6,38 | 5,02 | 5,88 |
| 7,15 | 5,53 | 7,35 | | 7,38 | 5,56 | 7,62 |
| 6,91 | 5,47 | 6,50 | | 7,63 | 6,21 | 7,82 |
| 6,40 | 4,95 | 6,77 | | 7,74 | 5,62 | 7,45 |
| 6,75 | 4,98 | 7,44 | | 6,61 | 4,92 | 6,64 |
| 7,06 | 5,48 | 6,98 | | | | |
Получим систему нормальных уравнений после подстановки соответствующих значений в (3.10) в виде:
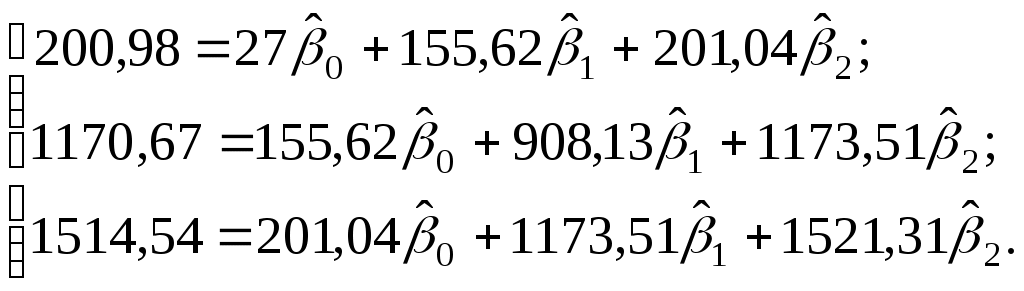
Решая последнюю систему методом Крамера, получим:
=1,11, =0,56, =0,41.Уравнение регрессии имеет вид:
Y=1,11+0,56X1+0,41X2.
Или, с учетом (3.8) и расчетов:
=0,75, =0,65, =0,96, =0,56 =0,48, =0,41 =0,52 уравнение регрессии в стандартизованном масштабе: .Нетрудно восстановить (учитывая, что A=
=3,03) исходную модель (3.9) .Эластичность выпуска продукции Q по труду L равна 0,56, а эластичность выпуска продукции Q по капиталу K равна 0,41. Следовательно увеличение затрат труда на 1% приведет к росту выпуска продукции на 0,56%, а увеличение затрат капитала на 1% приведет к росту выпуска продукции на 0,41%.
Очевидно, что обе величины
и должны находиться между нулем и единицей. Они должны быть положительными, так как увеличение затрат факторов должно вызывать рост выпуска. В то же время, вероятно, они будут меньше единицы, т.к. мы предполагаем, что уменьшение эффекта от масштаба производства приводит к более медленному росту выпуска продукции, чем затрат производственных факторов, если другие факторы остаются постоянными.