ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 130
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
m 3 = 2, m = 1; при m = 1 x2 = 2;
б) x1 = 1, еслиm 3 = 1, m = 2; при m = 2 x2 = 3;
в) x2 = 2, еслиm + 1 = 2, m = 3; при m = 3 x1 = 6;
г) x2 = 1, еслиm + 1 = 1, m = 2; при m = 2 x1 = 5.
Ответ: при m 0, m3, m2, m 1 x1 = m 3; x2 = m + 1;
при m = 0 уравнение не имеет смысла;
при m = 3 x = 6;
при m = 2 x = 5;
при m = 1 x = 2;
при m = 2 x = 3.
(обратите внимание, что в задачах 55, 56 одно требование, но сформулировано оно по-разному)
Решение:
x2 (2a 2)x 2a + 1 0. (2)
D1 = (a 1)2 (2a + 1) = a2 2a + 1 + 2a 1 = a2.
а) D1 0 при любых a; x1 = a 1 a = 1, x2 = a 1 + a = 2a 1.
x = a;
x 1,
x 2a 1.
a = 1; a = 1;
a = 2a 1, a =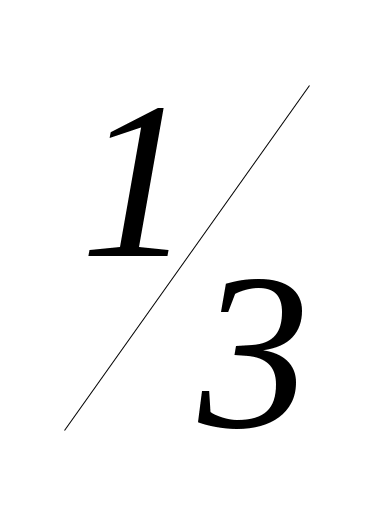 .
.
a = 4, a = 4.
Ответ: при a 4, a 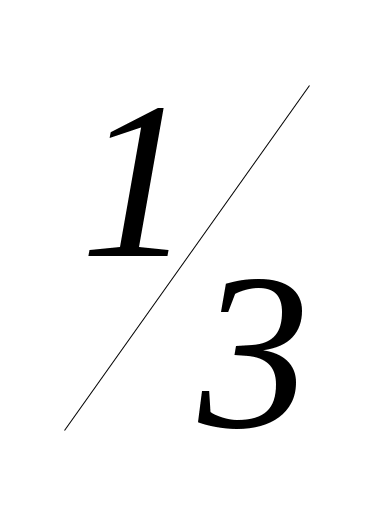 , a
, a
1, a 2,5 x1 = 4; x2 = a;
при a = 4, a = , a = 1, x = 4;
, a = 1, x = 4;
при a = 2,5 x = 2,5.
Решение:
x 3.
а) D= 0, но x 3.
D= 0, a2 4 = 0, a = 2.
Проверка: если a = 2, x2 + 2x + 1 = 0, x = 1.
если a = 2, x2 2x + 1 = 0, x = 1.
б) Если квадратное уравнение имеет два корня, один из которых равен 3.
x1 = 3, ( 3)2a (3) + 1 = 0,
9 + 3a + 1 = 0;
a = 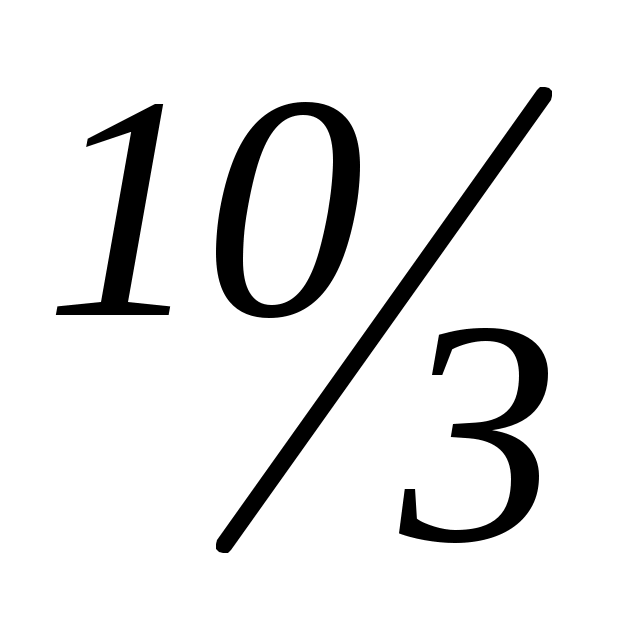 .
.
Найдем второй корень (самостоятельно): x2 = 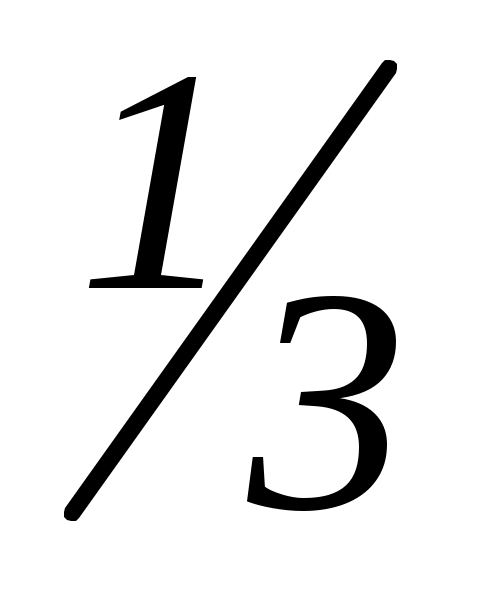 .
.
Ответ: a = 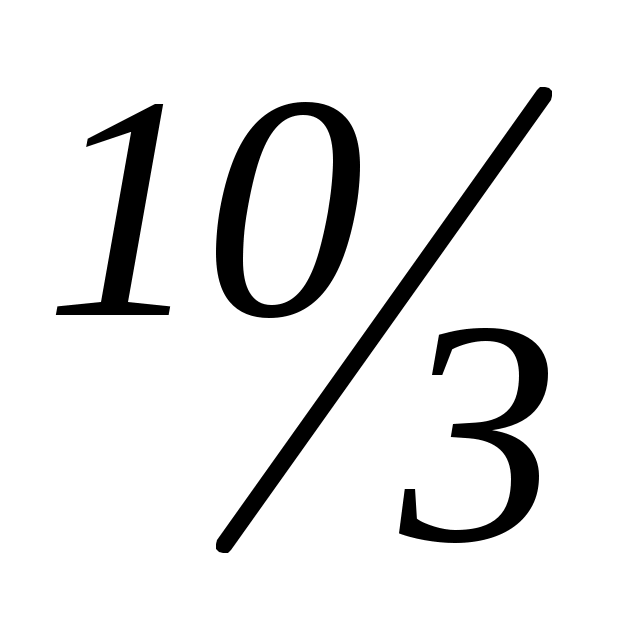 ; a = 2; a = 2.
; a = 2; a = 2.
К азбуке квадратного уравнения относится и теорема Виета, позволяющая выяснить для уравнения, имеющего корни, их знаки, сравнить корни по модулю и т.п.
Устные упражнения.
а) x2 7ax + 12a2 = 0; б) x2 + 5bx + 6b2 = 0; в) 7x2 4ax 3a2 = 0;
г) 7x2 + 13bx + 6b2 = 0; д) x2 (3a1)x + 2a2 a = 0; е) x2 (4b2)x + 3b2 2b = 0.
Далее целесообразно решить серию несложных задач.
Ответ: 3; 4.
Ответ: 1.
Ответ: p = q = 0 или p = 1, q = 6.
Более подробно следует остановиться на задачах такого содержания.
Обсуждаем. Для того, чтобы оба корня уравнения были положительны, нужно, во-первых, чтобы оно имело два корня, а для этого необходимо, чтобы дискриминант был больше нуля. Во-вторых, так как свободный член положительный, то оба корня имеют одинаковые знаки, а поэтому, чтобы они имели знаки "плюс", нужно, чтобы коэффициент среднего члена был отрицательный.
Разбив требование задачи на указанные две части, мы разбиваем и саму задачу на две более простые:
Решение:
a 2; a 2.
a 0.
Ответ: a 2.
а) положительные корни;
б) отрицательные корни;
в) корень, равный нулю?
Ответ: а) 0 a 2; б) 2 a 0; в) a = 0.
Решение: x2 x1 =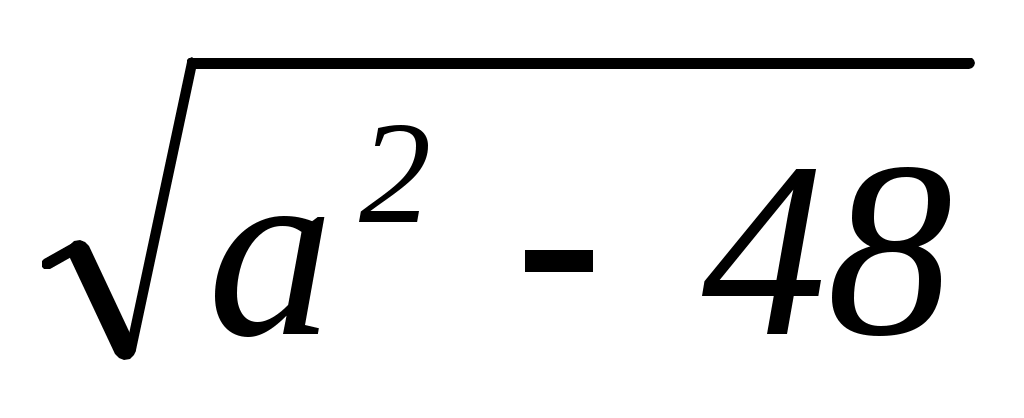 = 1, a = 7.
= 1, a = 7.
Ответ: a = 7.
Разнообразны задачи с применением формул сокращенного умножения.
Решение:
x1 x2 = a2.
Ответ: 4.
Решение:
a2 24 0, a2 24; a 2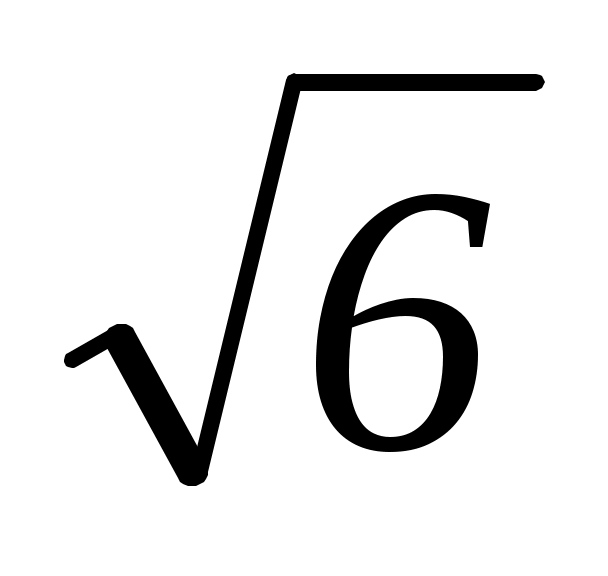 .
.
x1 x2 =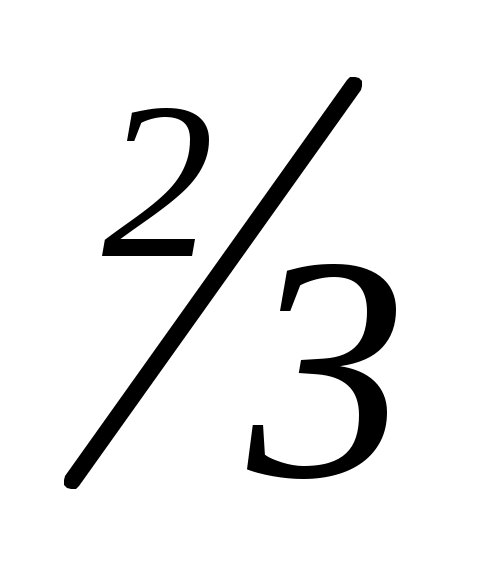 .
.
Ответ: 6.
Решение:
x1 x2 = q.
Ответ: p4 – 4p2q2 + 2q2.
Ответ: –1.
Ответ: 1.
Учащиеся должны самостоятельно уметь решать задачи типа 59, 62, 65. Задачи такого типа целесообразно включать как обязательный материал в текущие самостоятельные и контрольные работы.
Итоги работы за год покажет большая проверочная работа, в которую включены задачи, аналогичные ключевым по всем темам.
9 класс.
Основная цель работы в 9 классе – тщательно изучить квадратный трехчлен и квадратные неравенства. Учащиеся 9 класса уже готовы к серьезной исследовательской работе, поэтому излагать новый материал можно в виде проблемного диалога между учениками и учителем.
Квадратичная функция и ее график.
При изучении графиков функций y = ax2 + nиy = a(x – m)2 в устную и письменную работу полезно включать задачи такого содержания.
б) x1 = 1, еслиm 3 = 1, m = 2; при m = 2 x2 = 3;
в) x2 = 2, еслиm + 1 = 2, m = 3; при m = 3 x1 = 6;
г) x2 = 1, еслиm + 1 = 1, m = 2; при m = 2 x1 = 5.
Ответ: при m 0, m3, m2, m 1 x1 = m 3; x2 = m + 1;
при m = 0 уравнение не имеет смысла;
при m = 3 x = 6;
при m = 2 x = 5;
при m = 1 x = 2;
при m = 2 x = 3.
-
Для каждого значения параметра a решить уравнение: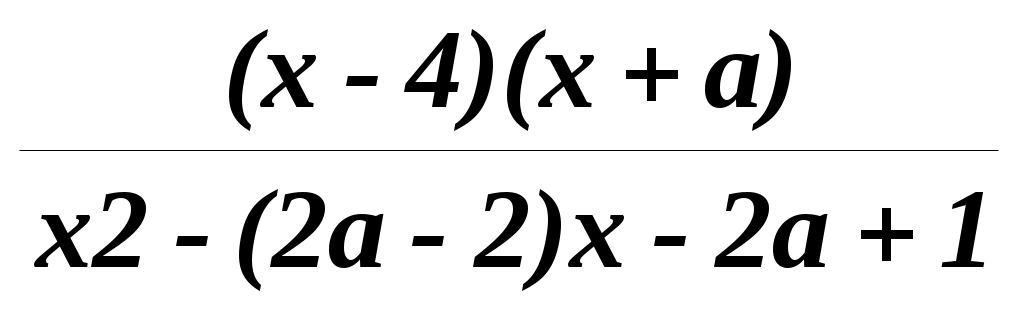 = 0.
= 0.
(обратите внимание, что в задачах 55, 56 одно требование, но сформулировано оно по-разному)
Решение:
-
Д анное уравнение равносильно системе (x 4)(x + a) = 0; (1)
анное уравнение равносильно системе (x 4)(x + a) = 0; (1)
x2 (2a 2)x 2a + 1 0. (2)
-
Решим квадратное уравнение (2),
D1 = (a 1)2 (2a + 1) = a2 2a + 1 + 2a 1 = a2.
а) D1 0 при любых a; x1 = a 1 a = 1, x2 = a 1 + a = 2a 1.
-
Т
 огда система принимает следующий вид: x = 4,
огда система принимает следующий вид: x = 4,
x = a;
x 1,
x 2a 1.
-
И
 сключим те значения a, при которых: 2a 1 = 4; a = 2,5;
сключим те значения a, при которых: 2a 1 = 4; a = 2,5;
a = 1; a = 1;
a = 2a 1, a =
a = 4, a = 4.
Ответ: при a 4, a
1, a 2,5 x1 = 4; x2 = a;
при a = 4, a =
при a = 2,5 x = 2,5.
-
При каких значениях a уравнение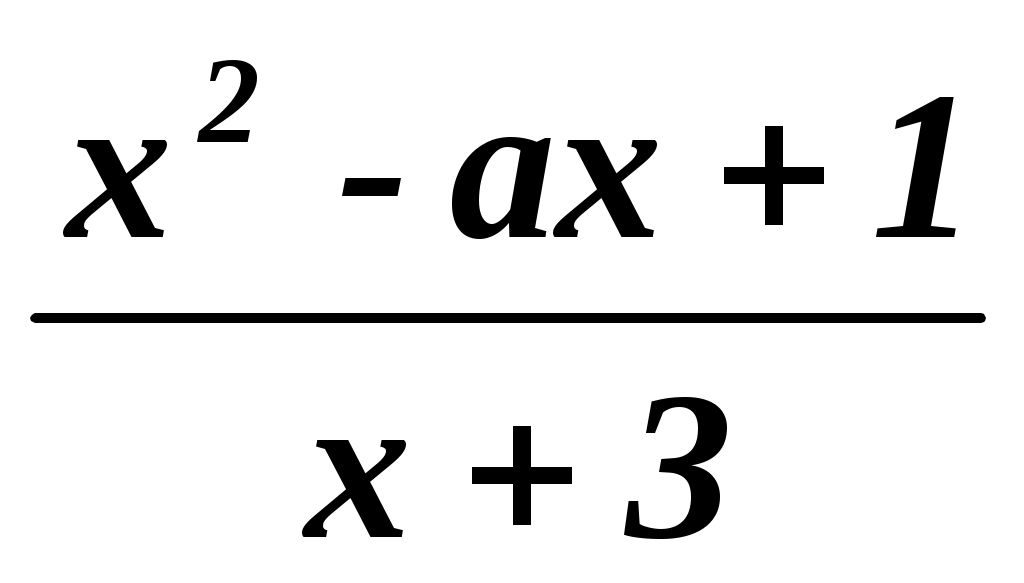 = 0 имеет единственное решение?
= 0 имеет единственное решение?
Решение:
-
Д анное уравнение равносильно системе x2 ax + 1 = 0,
анное уравнение равносильно системе x2 ax + 1 = 0,
x 3.
-
Уравнение имеет один корень, если
а) D= 0, но x 3.
D= 0, a2 4 = 0, a = 2.
Проверка: если a = 2, x2 + 2x + 1 = 0, x = 1.
если a = 2, x2 2x + 1 = 0, x = 1.
б) Если квадратное уравнение имеет два корня, один из которых равен 3.
x1 = 3, ( 3)2a (3) + 1 = 0,
9 + 3a + 1 = 0;
a =
Найдем второй корень (самостоятельно): x2 =
Ответ: a =
К азбуке квадратного уравнения относится и теорема Виета, позволяющая выяснить для уравнения, имеющего корни, их знаки, сравнить корни по модулю и т.п.
Устные упражнения.
-
Решите уравнение.
а) x2 7ax + 12a2 = 0; б) x2 + 5bx + 6b2 = 0; в) 7x2 4ax 3a2 = 0;
г) 7x2 + 13bx + 6b2 = 0; д) x2 (3a1)x + 2a2 a = 0; е) x2 (4b2)x + 3b2 2b = 0.
Далее целесообразно решить серию несложных задач.
-
При каких k произведение корней квадратного уравнения x2 + 3x + (k2 7k + 12) равно нулю?
Ответ: 3; 4.
-
При каких значениях k сумма корней квадратного уравнения x2 + (k2 + 4k 5)x k равна нулю?
Ответ: 1.
-
При каких значениях p и q корни уравнения x2 + px + q = 0 равны 2p и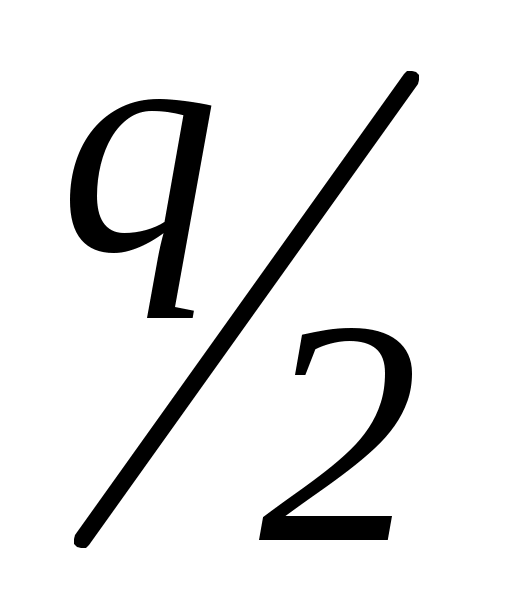 ?
?
Ответ: p = q = 0 или p = 1, q = 6.
Более подробно следует остановиться на задачах такого содержания.
-
При каких значениях a оба корня уравнения x2 2ax + 4 = 0 положительны?
Обсуждаем. Для того, чтобы оба корня уравнения были положительны, нужно, во-первых, чтобы оно имело два корня, а для этого необходимо, чтобы дискриминант был больше нуля. Во-вторых, так как свободный член положительный, то оба корня имеют одинаковые знаки, а поэтому, чтобы они имели знаки "плюс", нужно, чтобы коэффициент среднего члена был отрицательный.
Разбив требование задачи на указанные две части, мы разбиваем и саму задачу на две более простые:
-
При каких значениях a дискриминант уравнения положительный? -
При каких значениях a коэффициент среднего члена уравнения отрицательный?
Решение:
-
D= a2 4, a2 4 0, a2 4, a 2, a 2 или a 2. -
2a 0, a 0. -

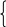 a 2,
a 2,
a 2; a 2.
a 0.
Ответ: a 2.
-
При каких значениях параметра a уравнение ax2 4x + a = 0 имеет:
а) положительные корни;
б) отрицательные корни;
в) корень, равный нулю?
Ответ: а) 0 a 2; б) 2 a 0; в) a = 0.
-
В уравнении x2 + ax + 12 = 0 определить a таким образом, чтобы разность корней равнялась единице.
Решение: x2 x1 =
Ответ: a = 7.
Разнообразны задачи с применением формул сокращенного умножения.
-
Корниуравнения x2 3ax + a2 = 0 таковы, что x1 2+ x2 2 = 112. Найти a.
Решение:
-
D= 9a2 4a2 = 5a2, D 0 при любых a. -
x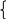 1 + x2 = 3a;
1 + x2 = 3a;
x1 x2 = a2.
-
x12+ x22 = (x1 + x2)2 2x1 x2 = (3a)2 2a2 = 7a2 = 112; a2 = 16, a = 4.
Ответ: 4.
-
В уравнении 3x2 + ax + 2 = 0 определить a таким образом, чтобы корни уравнения были действительными, а сумма кубов корней равнялась удвоенной сумме корней.
Решение:
-
D 0, D= a2 24;
a2 24 0, a2 24; a 2
-
x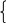 1 + x2 =
1 + x2 = 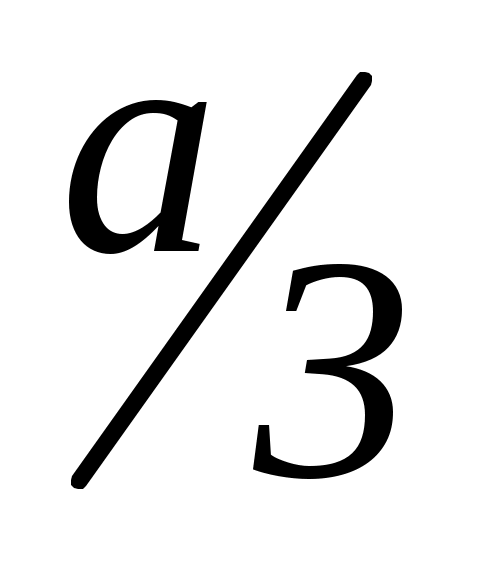 ;
;
x1 x2 =
-
x13+ x23 = (x1 + x2)(x12+ x22 x1 x2) = (x1 + x2)((x1+ x2)2 3x1 x2) = 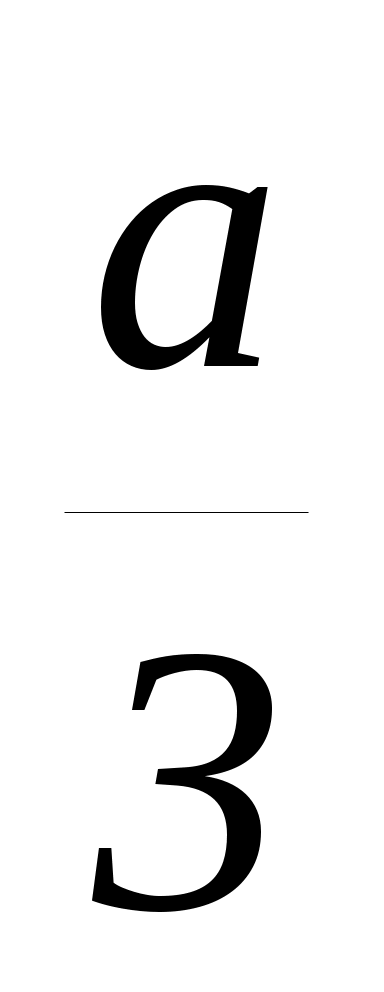 (
(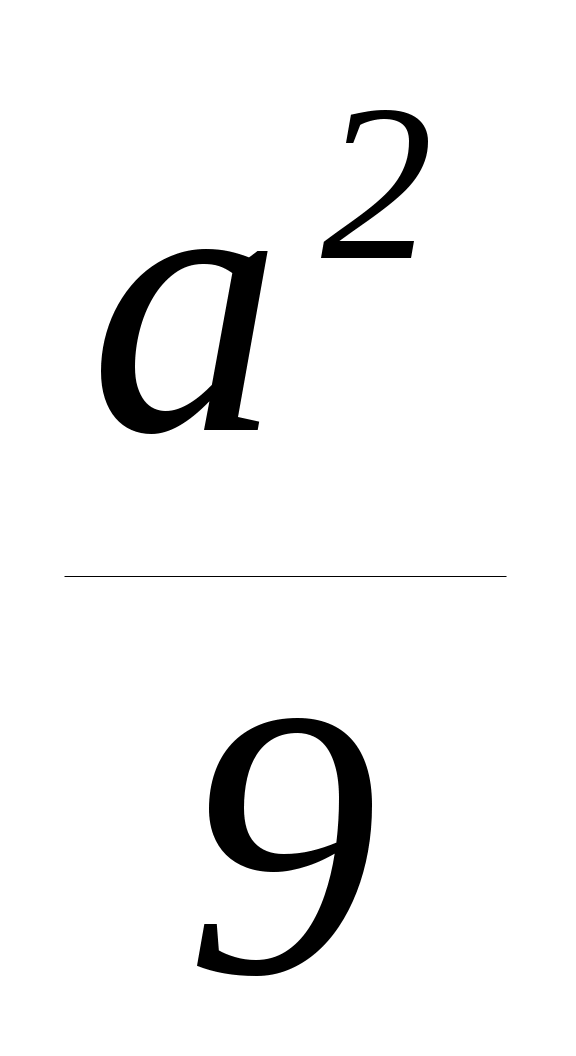 2).
2). -
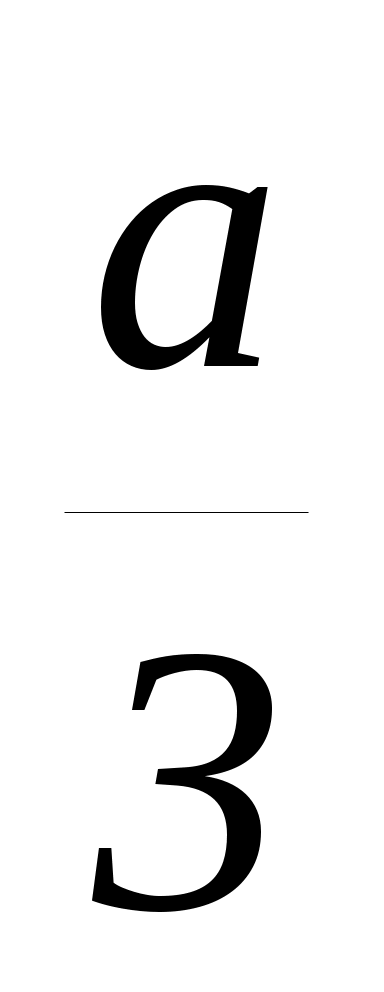 (
(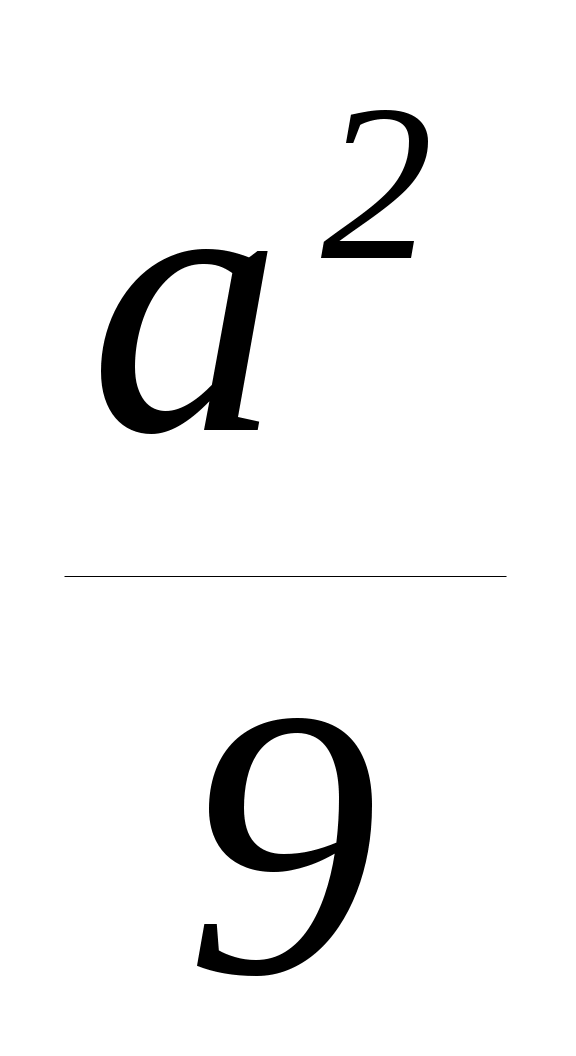 2) =
2) = 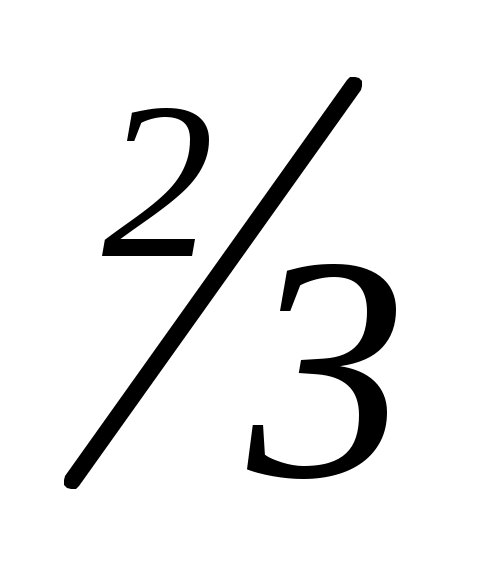 a; a(
a; a(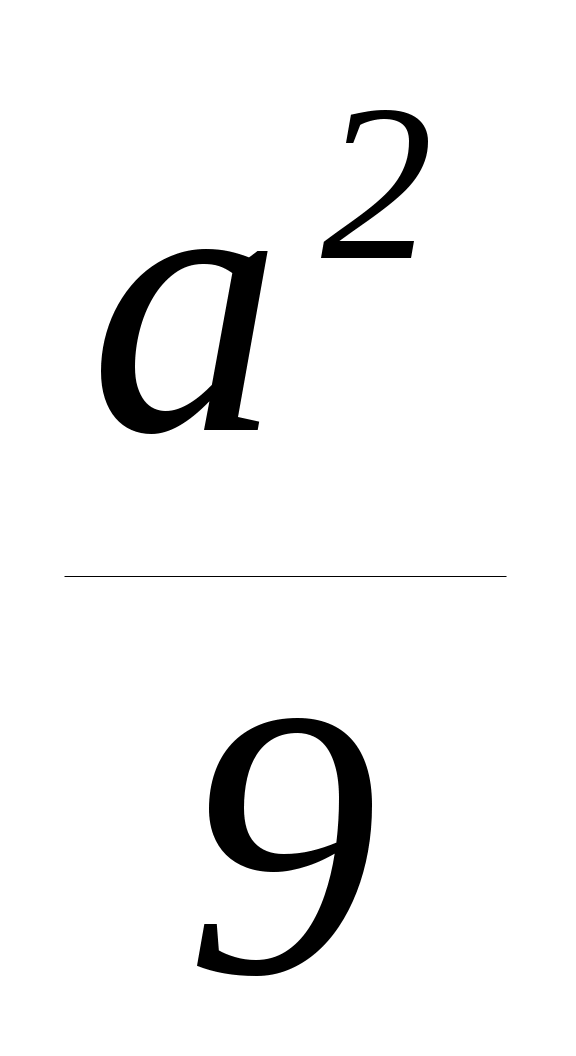 4) = 0; a = 0; a = 6.
4) = 0; a = 0; a = 6. -
0 2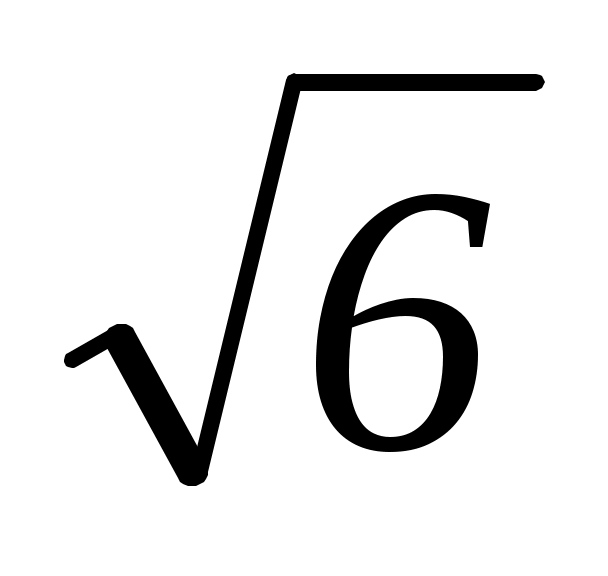 ; 6 2
; 6 2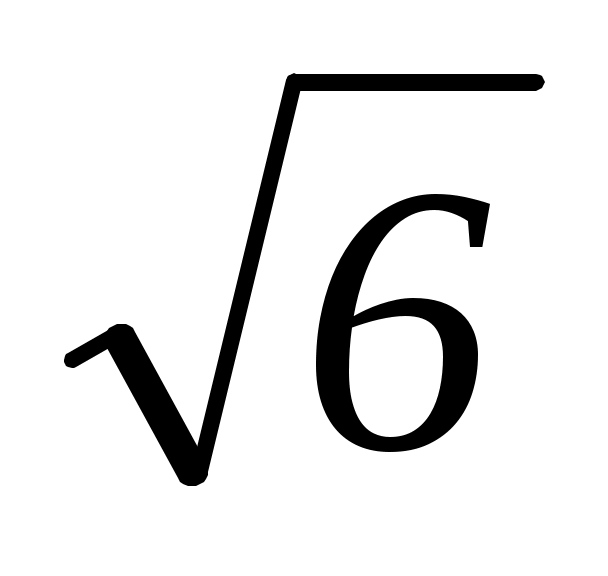 .
.
Ответ: 6.
-
Пусть x1 и x2– корниуравнения x2 + px + q = 0. Выразить x14+ x24 через p и q.
Решение:
-
x 1 + x2 = p;
1 + x2 = p;
x1 x2 = q.
-
x14+ x24 = (x12+ x22)2 2x12x22 = ((x1 + x2)2 2x1 x2)2 2x12x22 = (p2 – 2q2)2 – 2q2 = = p4 – 4p2q2 + 2q2.
Ответ: p4 – 4p2q2 + 2q2.
-
При каком значении параметра m сумма квадратов корней уравнения x2 + (m 1)x + m2 1,5 = 0 наибольшая?
Ответ: –1.
-
При каком значении параметра m сумма квадратов корней уравнения x2 + (2 m)x + m 3 = 0 наименьшая?
Ответ: 1.
Учащиеся должны самостоятельно уметь решать задачи типа 59, 62, 65. Задачи такого типа целесообразно включать как обязательный материал в текущие самостоятельные и контрольные работы.
Итоги работы за год покажет большая проверочная работа, в которую включены задачи, аналогичные ключевым по всем темам.
9 класс.
Основная цель работы в 9 классе – тщательно изучить квадратный трехчлен и квадратные неравенства. Учащиеся 9 класса уже готовы к серьезной исследовательской работе, поэтому излагать новый материал можно в виде проблемного диалога между учениками и учителем.
Квадратичная функция и ее график.
При изучении графиков функций y = ax2 + nиy = a(x – m)2 в устную и письменную работу полезно включать задачи такого содержания.
-
Найдите количество целых значений а, при которых абсцисса и ордината вершины параболы y = (x– 5 – a)2 + 3 – a положительны.