ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 128
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
8 класс.
Сейчас перед каждым учеником ставится задача научиться овладевать фундаментальными знаниями, т.е. не набором некоторых правил и умений решать стандартные задачи, а, прежде всего, глубокому пониманию сути изучаемых явлений, приобщению к поиску самих задач, постановке этих задач, формулированию гипотез, испытанию их на правдоподобие.
В процессе исследования ребята разрабатывают способы решения поставленной задачи, реализуют их, учатся обобщать полученные результаты, применять их для постановки новых проблем.
Уравнения с параметрами, приводимые
к линейным.
Следующий шаг в изучении уравнений с параметром, составляют уравнения, при решении которых требуется дополнительная проверка, связанная с ограничениями их области определения.
При изучении темы "Рациональные дроби" дается определение области допустимых значений переменных, а также условие равенства дроби нулю, что составляет базу для решения таких уравнений.
Прежде, чем заняться решением уравнений, мы опять возвращаемся к основам темы "Решение задач с параметрами", но уже на более серьезном теоретическом уровне.
Рассмотрим уравнения:
Каждое из этих уравнений можно рассматривать как уравнение с переменными x и a. Однако мы говорим о решении уравнения относительно x, считая x и a неравноценными, и хотим выразить x через a, считая a известным. При таком рассмотрении переменная x называется неизвестным, переменная a – параметром.
Если параметру, содержащемуся в уравнении, придать некоторое значение, то возможен один из двух случаев:
-
получится уравнение, содержащее лишь данные числа и неизвестные и не содержащее параметров; -
получится условие, лишенное смысла.
В первом случае значение параметра называется допустимым, во втором – недопустимым.
(обсудить предъявленные уравнения)
Решить уравнение, содержащее параметр – значит, для каждого допустимого значения параметра найти множество всех корней данного уравнения.
Условились параметры обозначать первыми буквами латинского алфавита: a, b, c, …, k, l, m, а неизвестные – последними: x, y, z.
Перейдем к рассмотрению ключевых уравнений.
(подобрать подготовительный материал для устной работы очень легко)
-
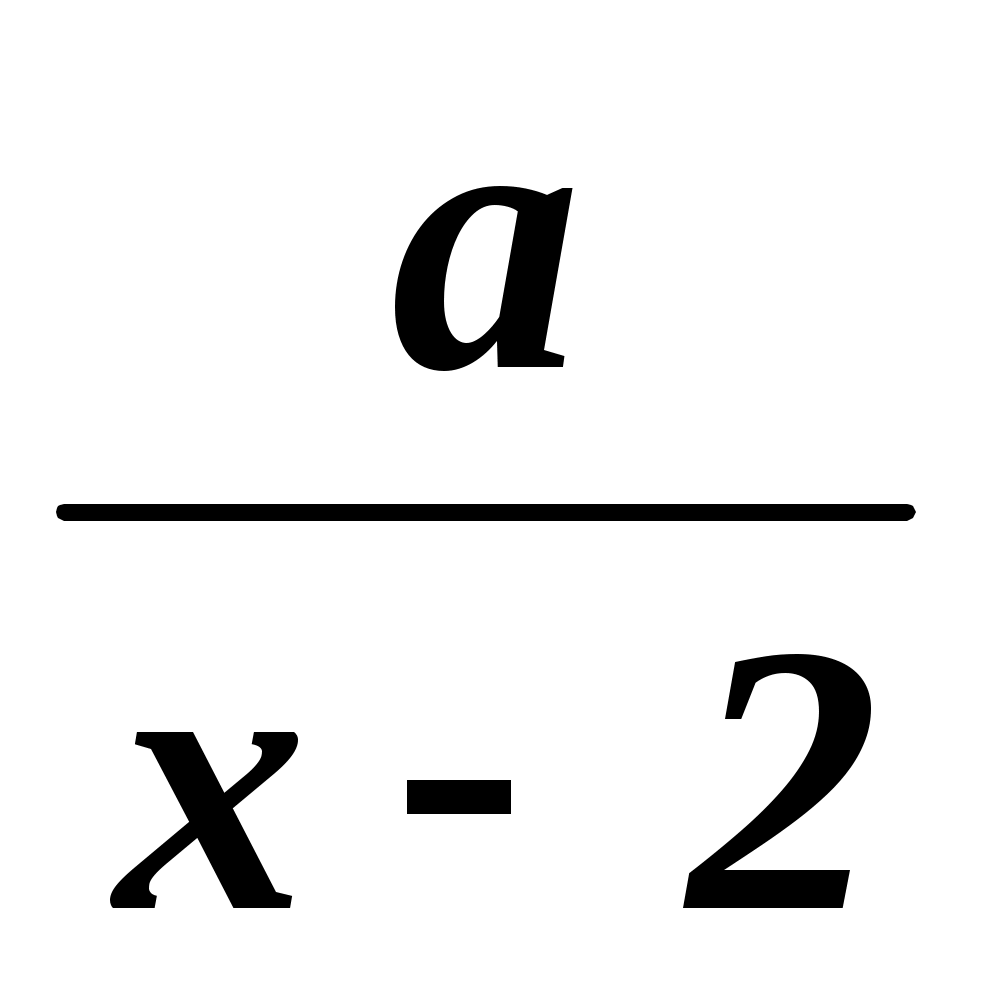 = 1.
= 1.
Решение:
-
ОДЗ: x 2. -
Умножим обе части уравнения на x 2 0, получим:
a = x 2,
x = a + 2.
-
Найдем недопустимые значения a, т.е. решим уравнение:
a + 2 = 2,
a = 0.
(Комментируем: при a = 0 x = 2, но число 2 не входит в область допустимых значений исходного уравнения, следовательно, не может быть его корнем).
Ответ: при a 0 x = a + 2;
при a = 0 корней нет.
-
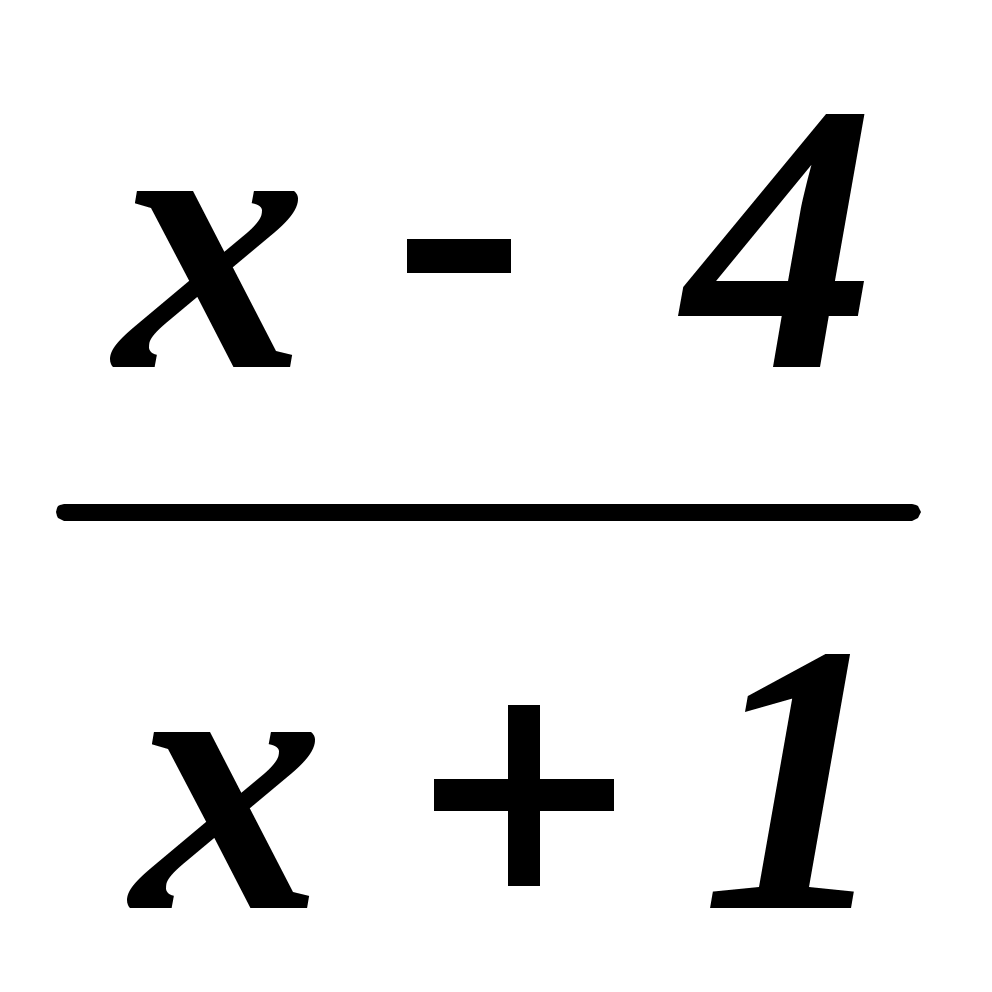 +
+ 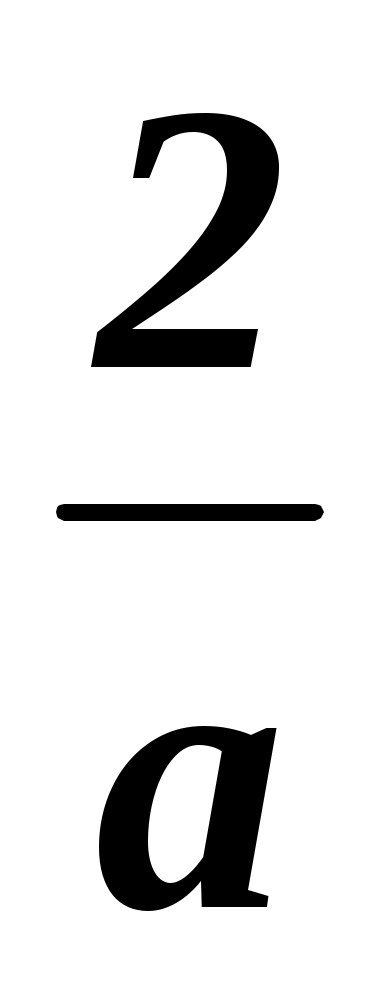 =
= 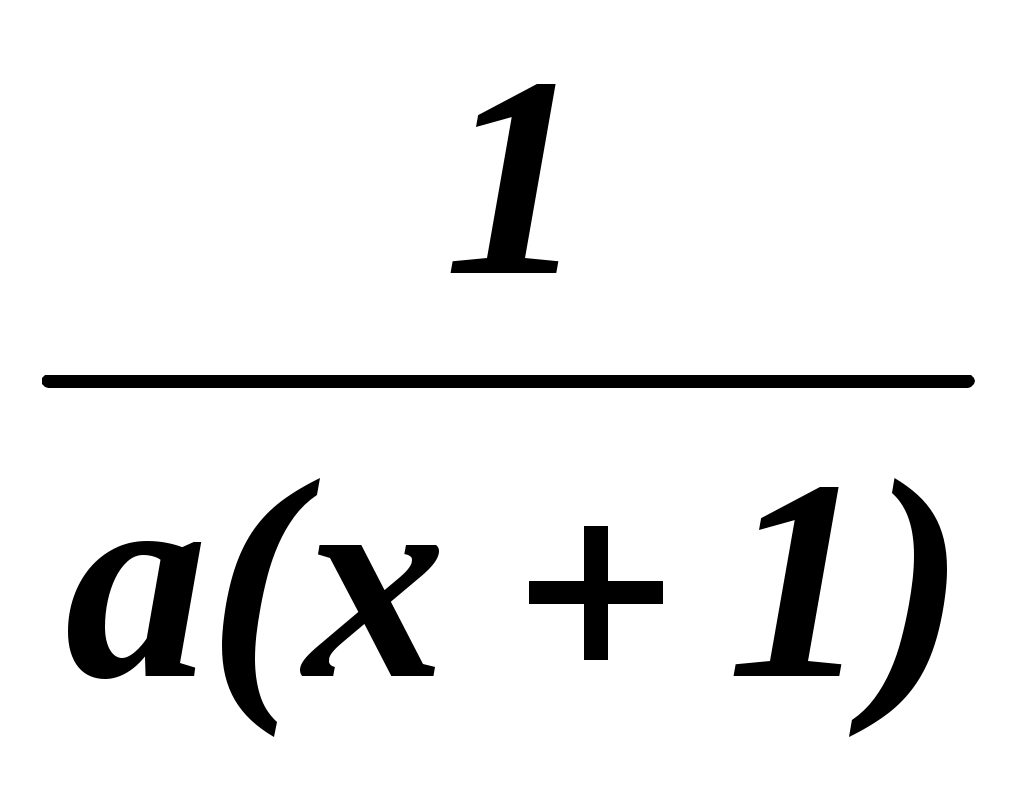 .
.
Решение:
-
ОДЗ: x 1, a 0. -
Умножим обе части уравнения на a (x + 1) 0, получим:
a (x – 4) + 2x + 2 = 1,
(a + 2) x = –1 + 4a. (1)
-
Найдем недопустимые значения a:
(комментарий: подставим x = –1 в уравнение (1)):
(a + 2) (–1) = –1 + 4a,
–a – 2 = –1
–5a = 1,
a = –
При a = –
(Комментарий: решим уравнение (1), это линейное уравнение относительно x, решение которого изучено в 7 классе.)
-
(a + 2) x = –1 + 4a
1. Если a + 2 0, a –2, то x =
2. Если a + 2 = 0, a = –2, то
0 x = – 9,
корней нет.
(Комментарий: обратите серьезное внимание на выписку ответа, можно упустить некоторые моменты).
Ответ: при a –2, a –
при a = –2, a = –
Вторую часть ответа можно выписать и следующим образом:
при a = –2, a = –
при a = 0 левая и правая части уравнений не имеют смысла.
-
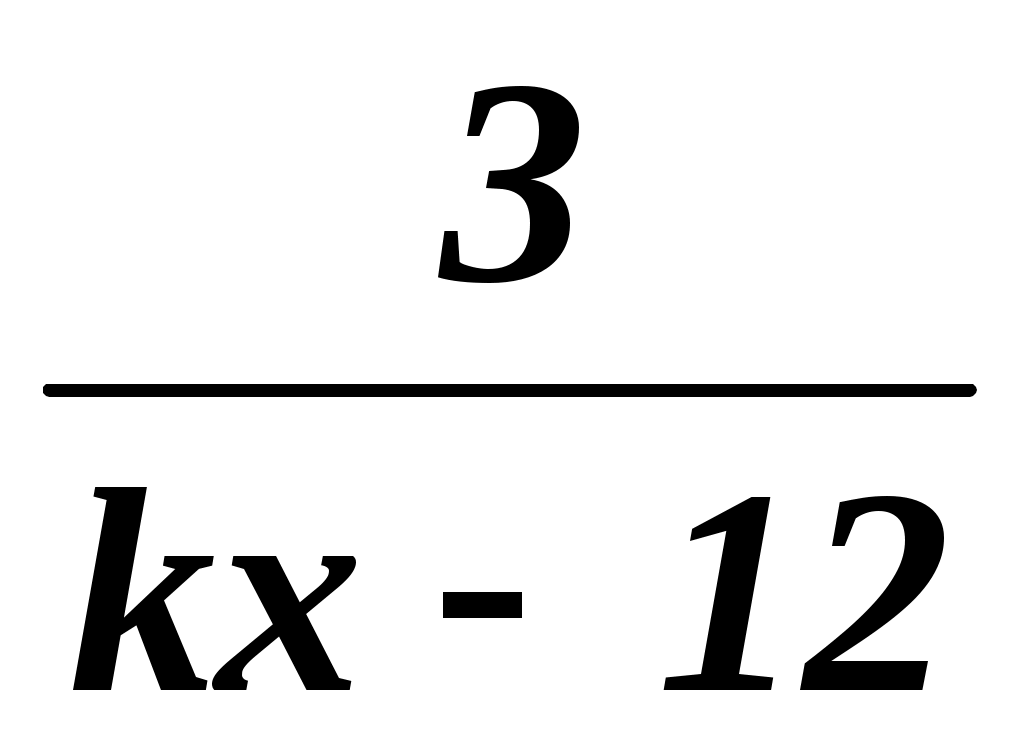 =
= 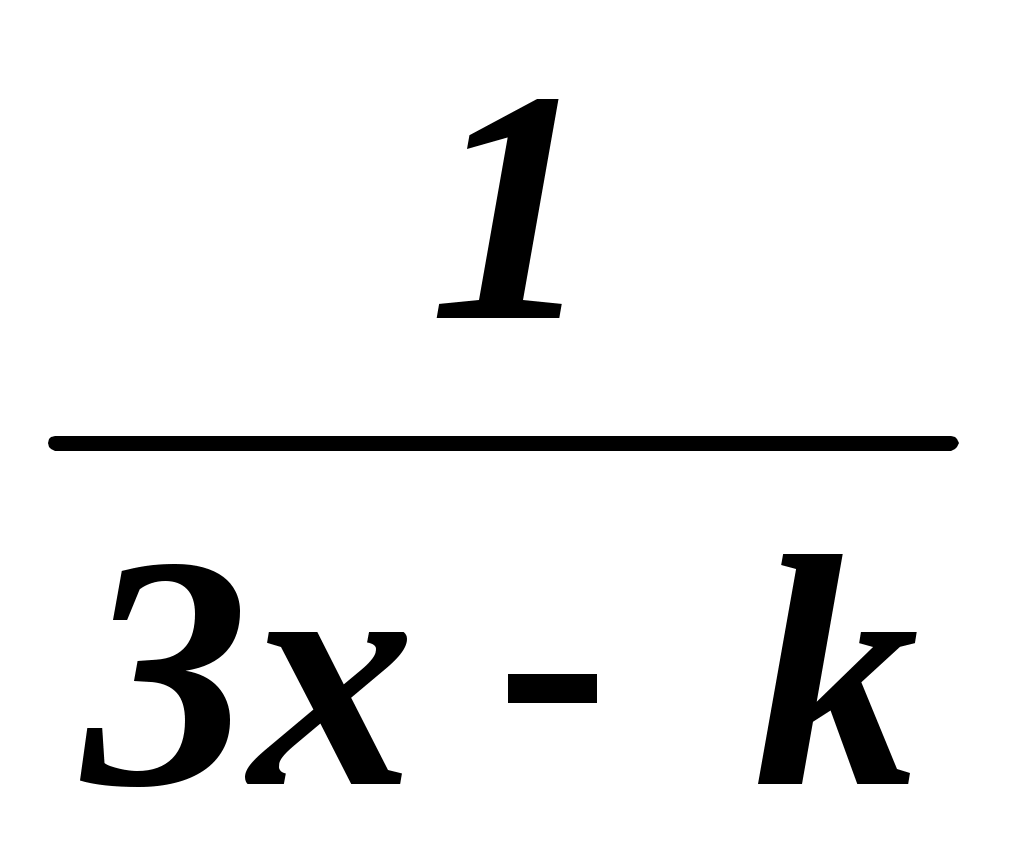 .
.
Решение:
-
ОДЗ: kx 12 0;x 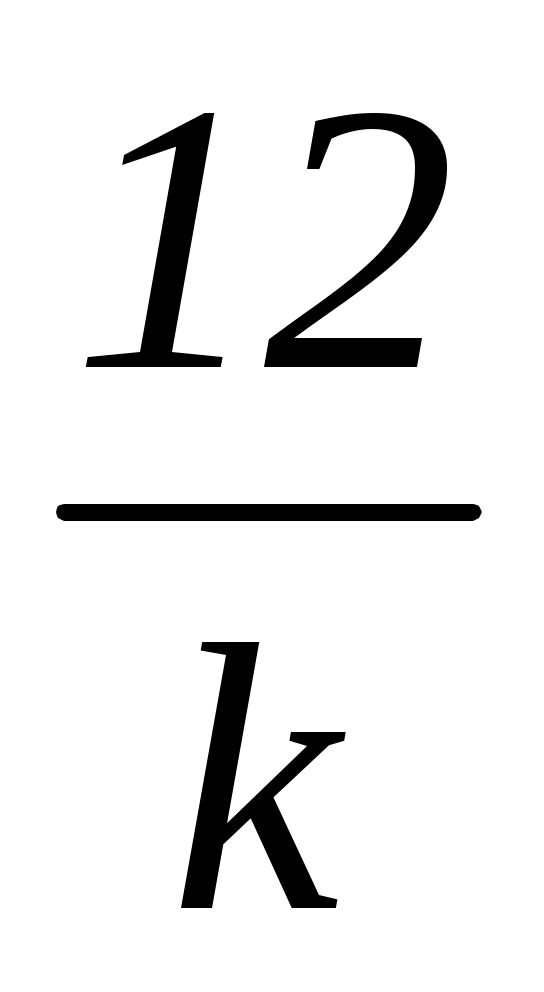 ;
;
3x – k 0; x
-
Умножим обе части уравнения на (kx – 12) (3x – k) 0, получим:
3 (3x – k) = kx – 12,
9x – 3k = kx – 12,
9x – kx = 3k – 12,
(9 – k) x = 3k – 12. (1)
-
Найдем недопустимые значения k:
1. Если x =
108 – 12k= 3k2 – 12,
k2 = 36,
k = 6.
2. Если x =
9k – k2 = 9k – 36,
k2 = 36,
k = 6.
При k = 6 корней нет.
-
Решим уравнение (9 – k) x = 3k – 12.
1. Если 9 – k 0, k 9, то x =
2. Если 9 – k = 0, k = 9, то
0 x = 15,
корней нет.
Ответ: при k 6, k 6, k 15 x =
при k = 6, k = 6, k = 15 корней нет.
Каждое из этих трех уравнений должно быть основательно проработано в классе, так как в их решении есть "подводные камни", которые должны преодолеть восьмиклассники.
Далее можно предложить учащимся самостоятельно составить словесное описание алгоритма решения таких уравнений.
Алгоритм решения уравнения с параметрами,
сводящегося к линейному.
-
Найти область допустимых значений неизвестного и параметров, входящих в уравнение. -
Умножить обе части уравнения на общий знаменатель, преобразовать к виду линейного. -
Найти недопустимые значения параметра. -
Решить линейное уравнение с параметром. -
Выписать ответ с учетом пунктов 3, 4.
Для формирования навыка решим следующие уравнения:
-
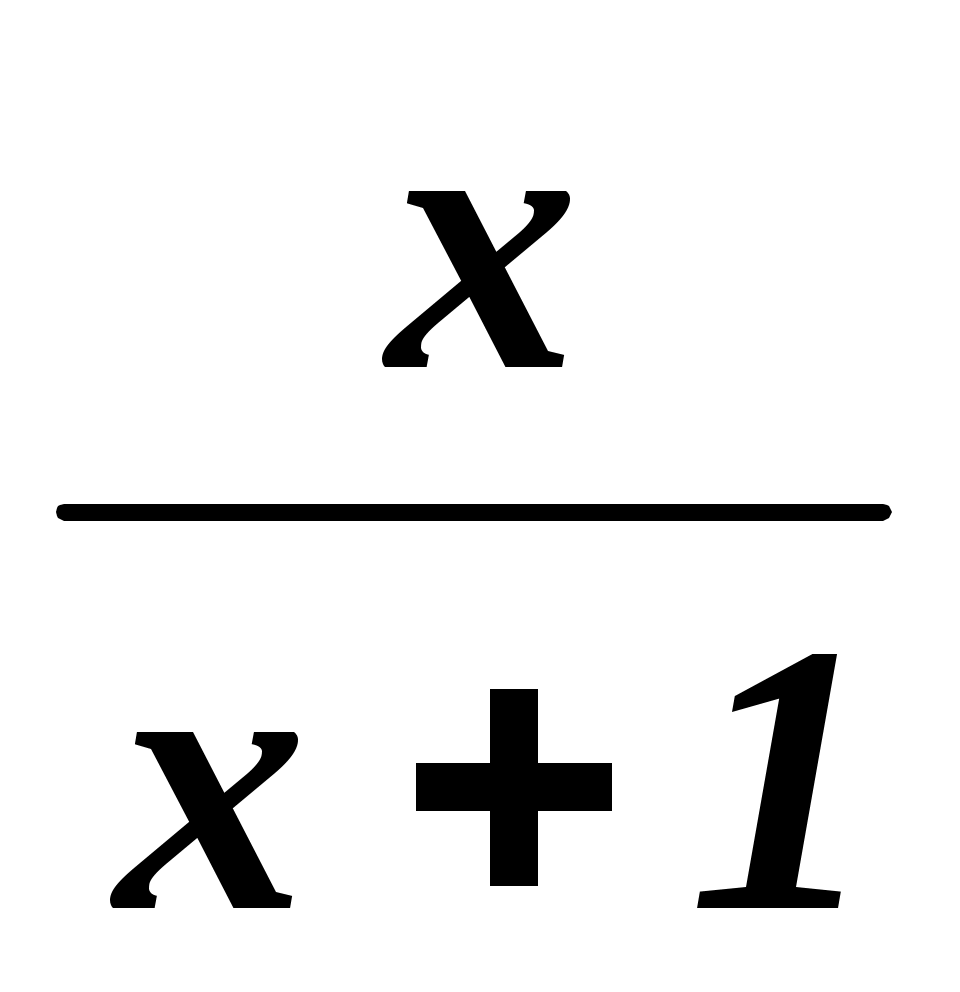 = a.
= a.
Решение:
-
ОДЗ: x –1; -
Умножим обе части уравнения на x + 1 0, получим:
x = a (x + 1),
x = ax + a,
x – ax = a,
(1 – a) x = a.
-
Найдем недопустимые значения a:
Если x = –1, то (1 – a) (– 1) = a, a – 1 = a, 0 a = 1, корней нет.
Не существует значений a, при которых x = –1.
-
(1 – a) x = a.
1. Если 1 – a 0, a1, то x =
2. Если 1 – a = 0, a = 1, то 0 x = 1, корней нет.
Ответ: при a 1 x =
при a = 1 корней нет.
-
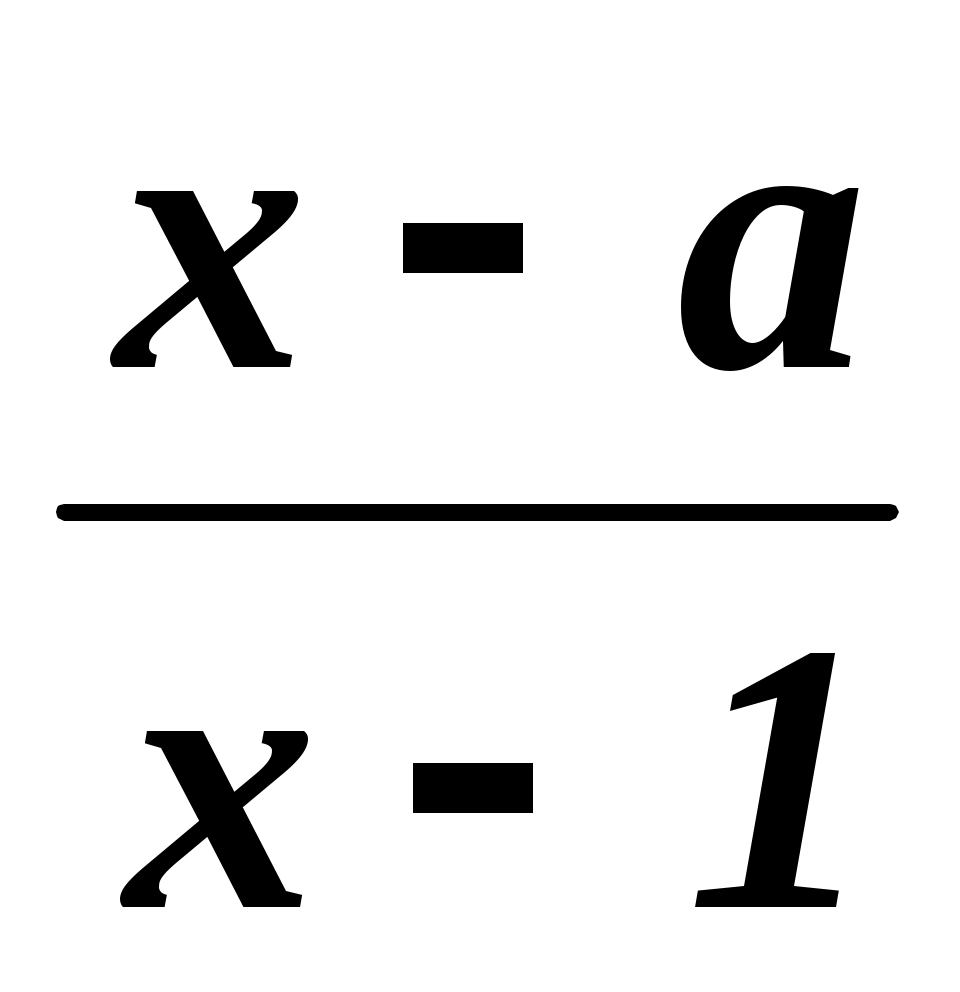 = 0.
= 0.
Ответ: при a 1 x = a;
при a = 1корней нет.
-
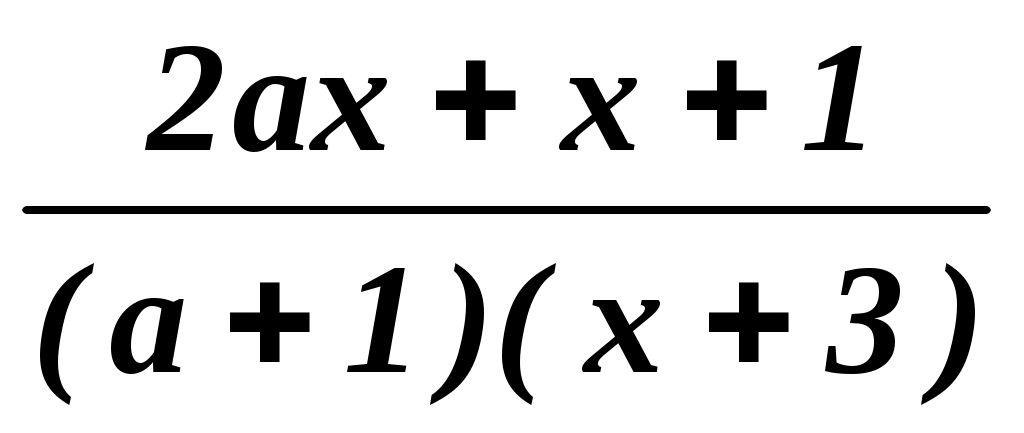 =
= 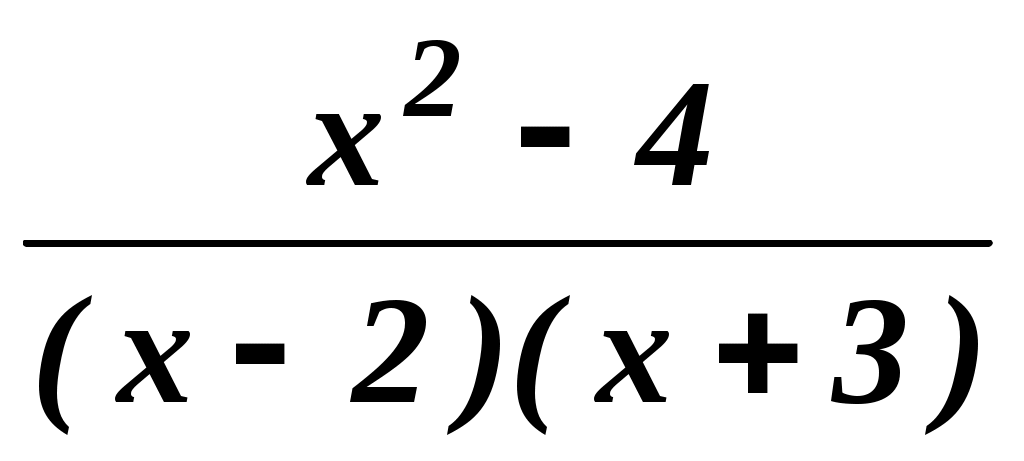 –
– 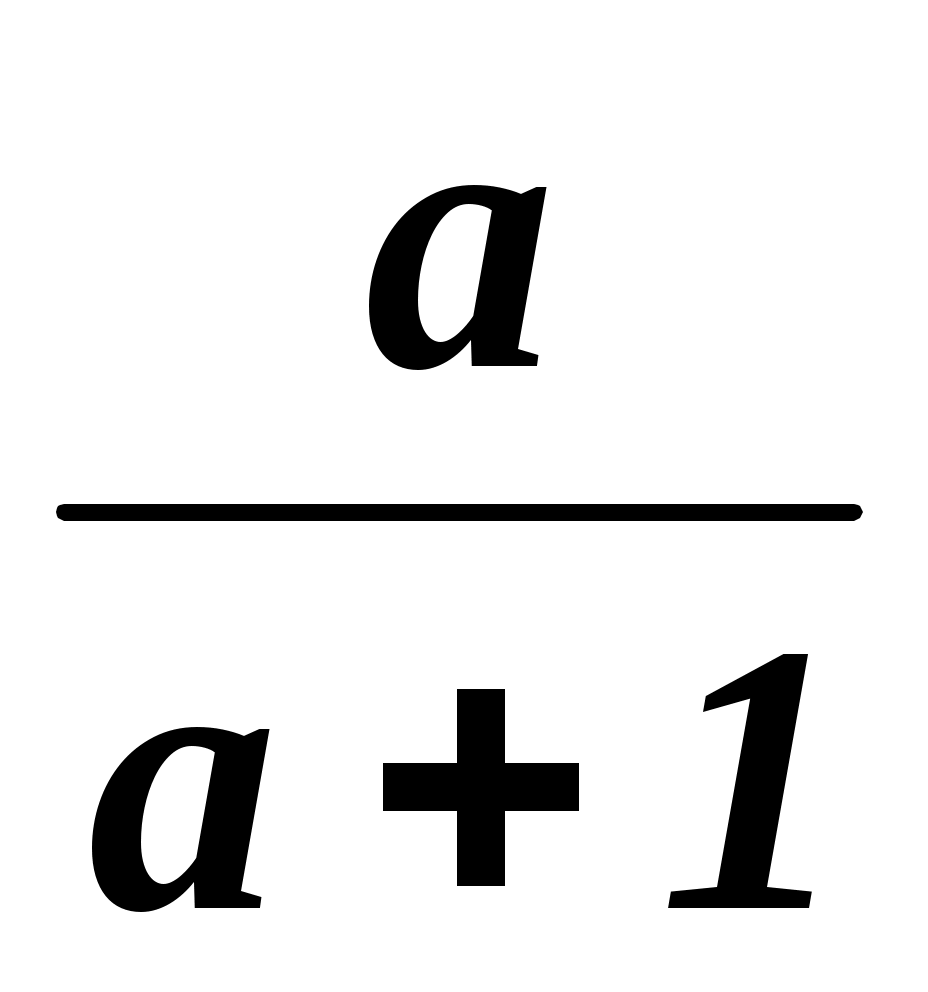 .
.
Решение:
-
ОДЗ: x –3; x 2;
a –1;
-
Упростим уравнение:
=
После преобразований, которые учащиеся выполняют самостоятельно, получим:
2ax = 1 – a.
-
Найдем недопустимые значения a:
1. Если x = –3, то 2a (–3) = 1 – a,
–6a = 1 – a,
–5a = 1,
a = –0,2.
2. Если x = 2, то 2a 2 = 1 – a,
5a = 1,
a = 0,2.
При a = 0,2 корней нет.
-
2ax = 1 – a.
1. Если 2a 0, a0, то x =
2. Если 2a = 0, a = 0, то 0 x = 1, корней нет.
Ответ: при a –1, a 0,2, a 0 x =
при a = –1, a = 0,2, a = 0корней нет.
-
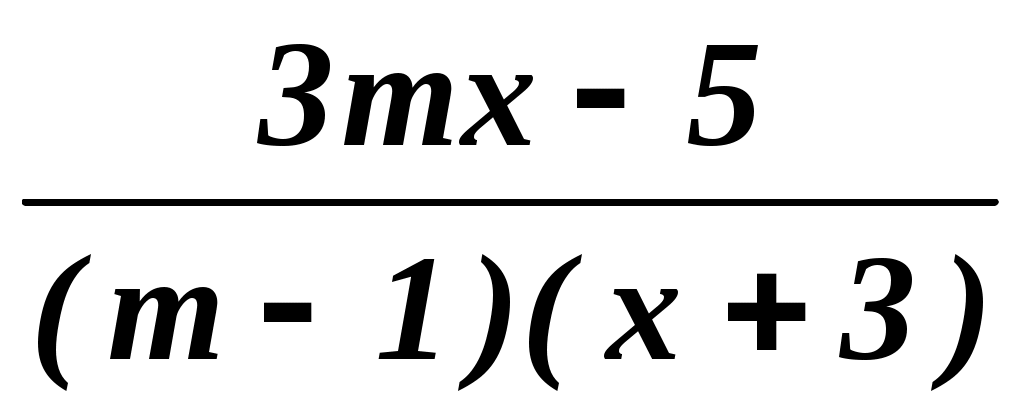 +
+ 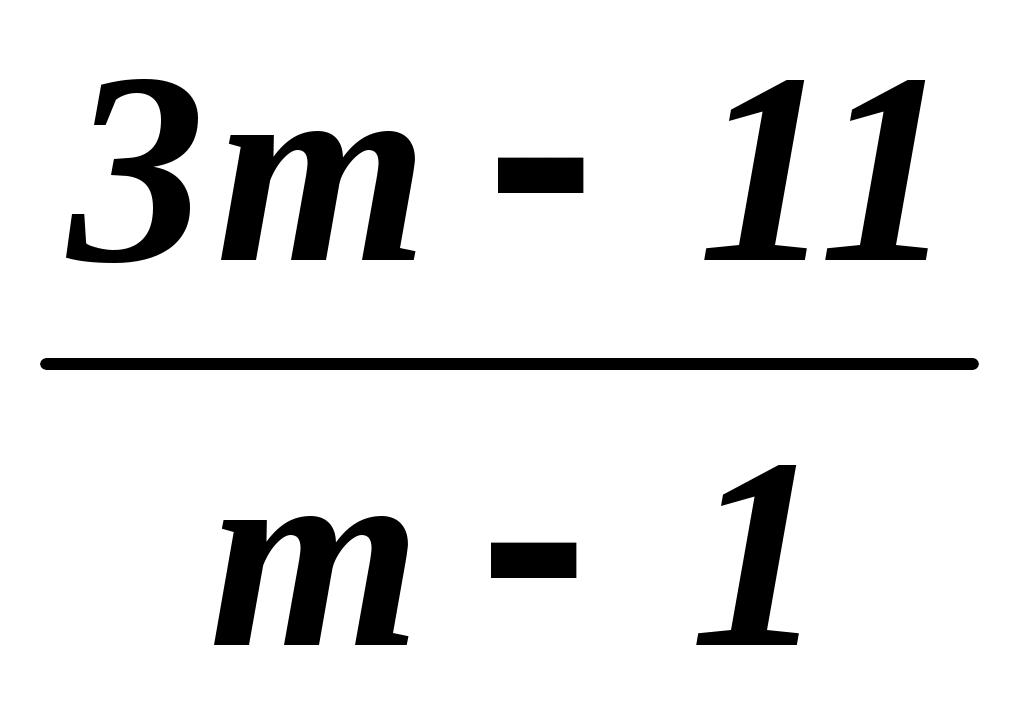 =
= 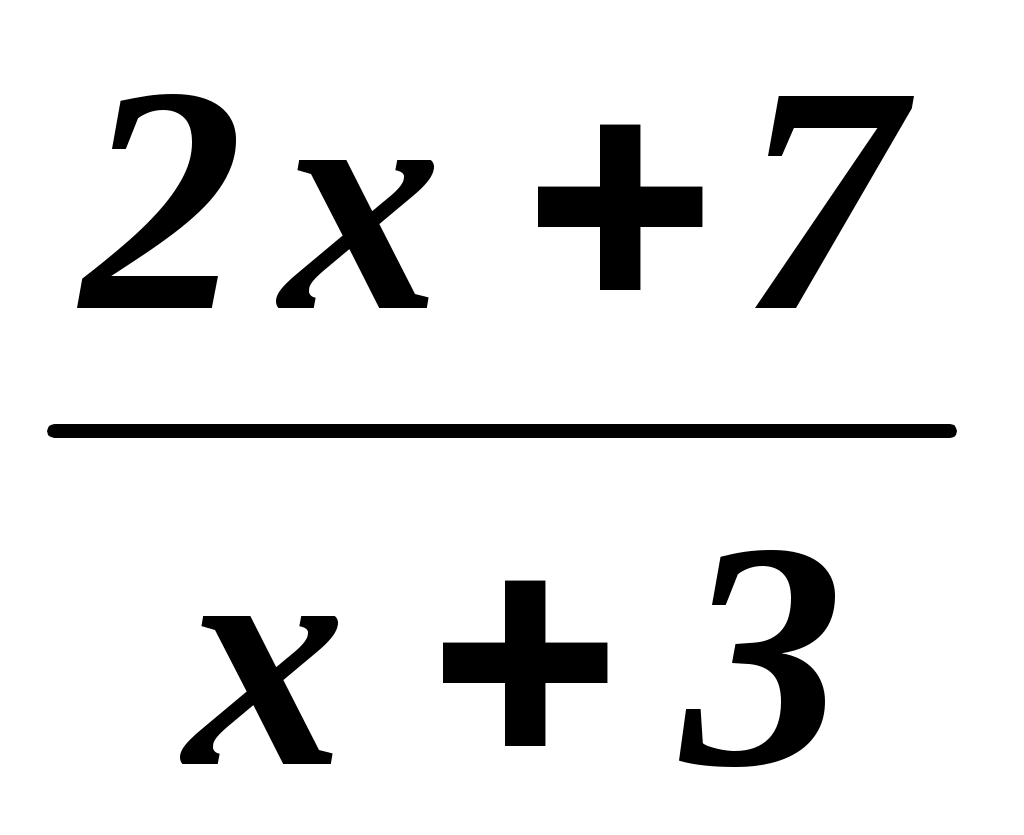 .
.
Ответ: при m 1, m –0,4 , m 2,25 x =
при m = –0,4 , m = 2,25 , корней нет;
при m = 1 уравнение не имеет смысла.
Следующие два уравнения можно отнести в банк задач и рассмотреть их решение в любое удобное время вплоть до 11 класса.
-
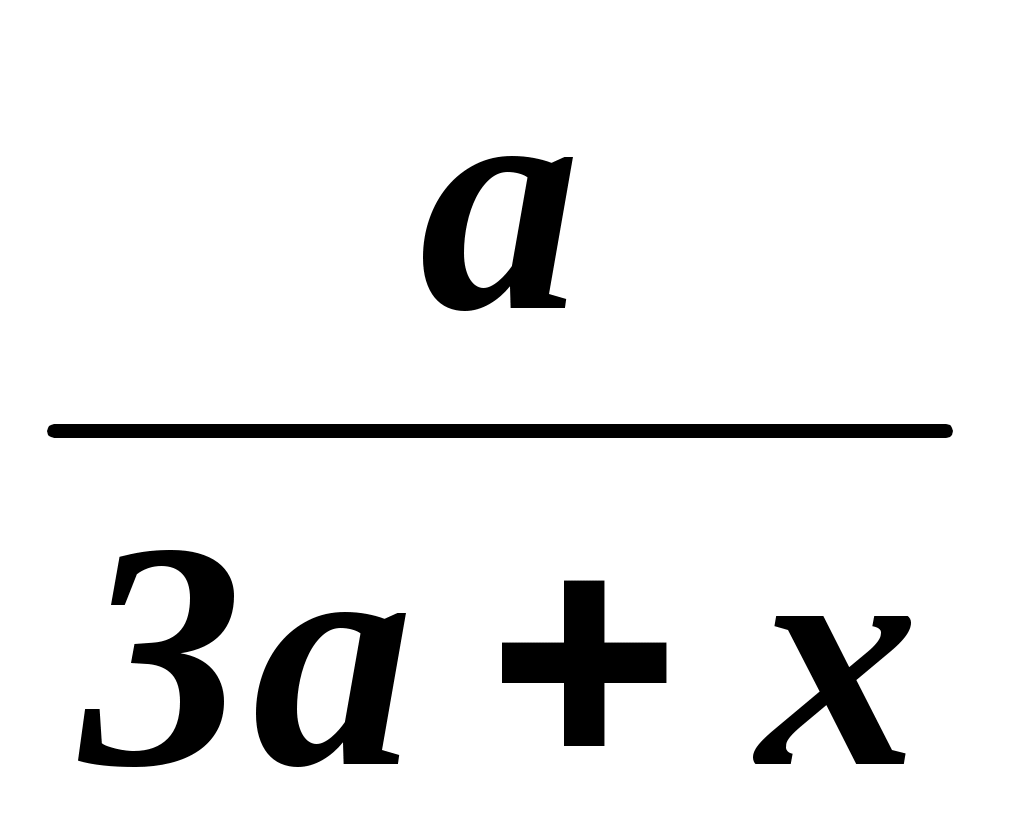 =
= 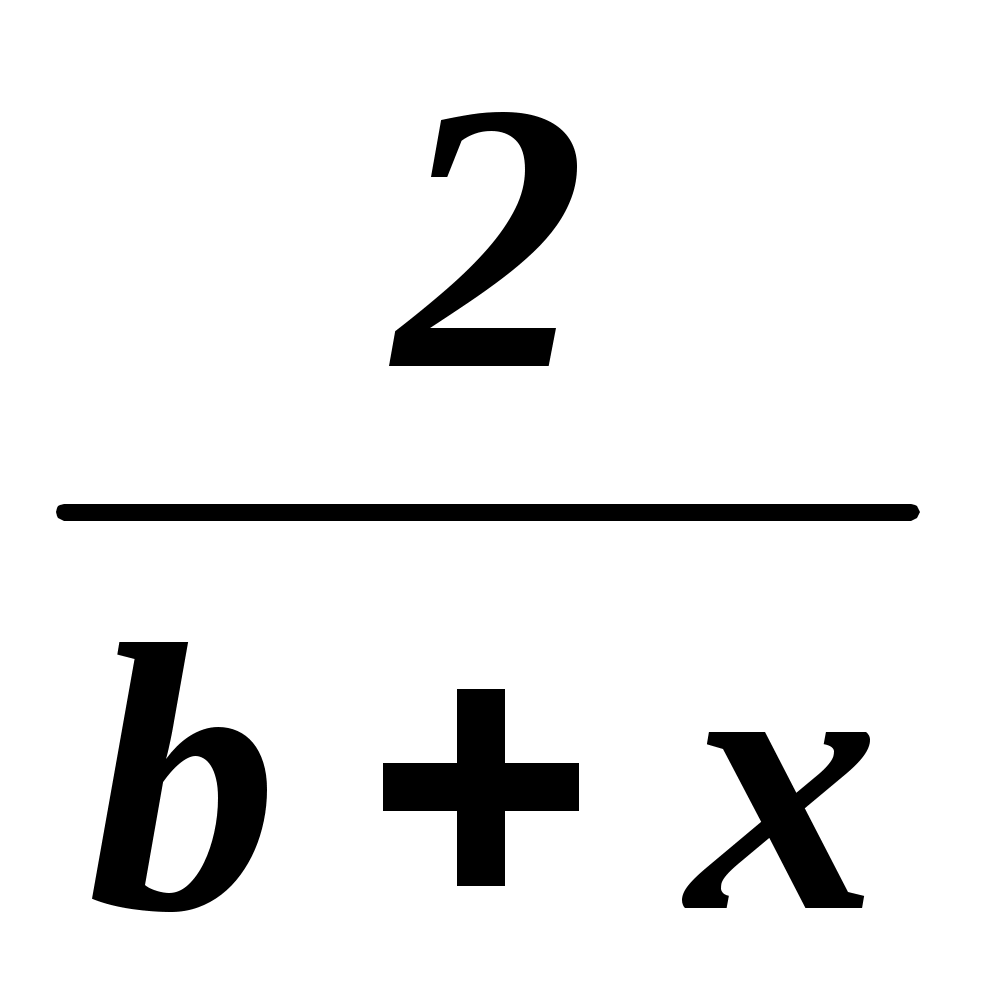 .
.
Решение:
-
ОДЗ: x –3a; x –b. -
a (b + x) = 6a + 2x,
(a – 2) x = a (6 – b).
-
Найдем недопустимые значения aи b:
1. Если x = –3a, то (a – 2) (–3a) = a (6 – b);
a (b – 3a) = 0;
 a = 0,
a = 0,b = 3a.
2. Если x = –b, то (a – 2) (–b) = a (6 – b),
2b = 6a,
b = 3a.
При a = 0 и b = 3aкорней нет.
-
(a – 2) x = a (6 – b).
1. Если a – 2 0, a2, то x =