ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 300
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Содержание третьего закона более глубоко раскрывается с помощью статистической теории и представлений квантовой теории строения вещества. В 1872 году австрийский физик Больцман первым пришел к заключению о том, что энтропия является функцией только термодинамической вероятности (или мультиплетности) W и что это соотношение должно быть логарифмическим:

S = k lnW, (1.121)
где k – постоянная Больцмана (k = R/NA). Мультиплетность W равна числу различных способов размещения структурных частиц системы (или вещества) при нахождении ее при данных термодинамических параметрах. В качестве наглядного представления о величине W рассмотрим схему двумерного кристалла (рис.1.14).


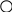


а) б)
Р
 ис.1.14. Схемы двумерных кристаллов из атомов А и В (а) и только из атомов А (б): – атомы А; – атомы В
ис.1.14. Схемы двумерных кристаллов из атомов А и В (а) и только из атомов А (б): – атомы А; – атомы В
Допустим, что в узлах кристалла находятся атомы одного и того же элемента – изотопы А и В (а). Энергия взаимодействия между ними одинакова, поэтому независимо от того, в каких узлах и какие атомы находятся, энергия и состояние кристалла при одних и тех же р и Т будут одинаковыми. Допустим также, что при некотором значении Т атомы А и В могут перескакивать вследствие диффузии из одного узла в другой. Вычислим, сколькими способами можно реализовать данное состояние. Очевидно, что два состояния кристалла будут при размещении атомов В по диагоналям кристалла и четыре состояния кристалла будут при размещении атомов В вдоль каждой из сторон кристалла. Всего шесть состояний – это и есть величина
W. Значение энтропии такого кристалла будет равно S=1,381·10-23 Дж/К ln6 = 2,47 ·10-23 Дж/К. Если бы рассматриваемый кристалл состоял только из атомов А (б), то при абсолютном нуле температуры в этом случае возможно было бы только одно состояние – когда атомы А находятся в узлах кристаллической решетки, то есть W=1. Тогда по формуле (1.121) энтропия равна нулю
S = k ln1 = 0,
что находится в соответствии с третьим законом термодинамики.
Абсолютную энтропию газа при температуре Т можно вычислить, интегрируя dqобр/Т от 0 К до заданной температуры. Если известны теплоемкости, энтальпия плавления в точке плавления Тпл и энтальпия испарения в точке кипения Ткип, то абсолютная энтропия при температуре Т может быть рассчитана по уравнению (1.122):
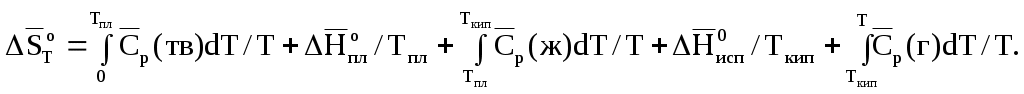 (1.122)
(1.122)
Если твердое тело находится в разных модификациях и их взаимное превращение сопровождается изменением энтальпии, то в сумму (1.121) нужно включить соответствующие энтропии фазовых превращений. Четвертое слагаемое (1.122) представляет собой мольную энтропию испарения. В стандартных условиях в точках кипения для многих жидкостей она постоянна и равна примерно 88кДж/(моль К):
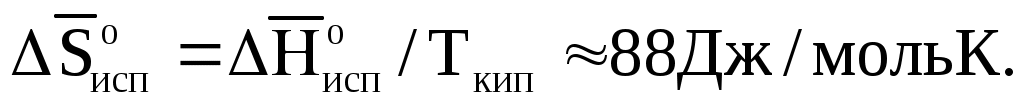 (1.123)
(1.123)
Это уравнение, известное как правило Трутона, полезно для оценки мольной теплоты испарения жидкостей с известными точками кипения.
1.3.10. Химический потенциал
В случае открытых систем в них могут вводиться или из них могут выводиться какие-то вещества. В частности, при протекании химических реакций изменяются числа молей компонентов в системах. В таких случаях энергия Гиббса каждой системы зависит не только от р и Т, но и от количеств веществ, а ее полный дифференциал через частные производные имеет следующий вид:
k
dG = (G/T) dT + (G/p)
dT + (G/p) dp + (G/ni)
dp + (G/ni)
dni , (1.124)
i=1
где k – число различных веществ; n1, n2, n3 … nk – числа молей веществ; ni – число молей вещества i; j i – это значит, что в производных под знаком суммирования сохраняются постоянными числа молей всех компонентов, кроме i-го. Можно показать, что первые две производные в скобах уравнения (1.124) соответственно равны – S и V. Поэтому вместо (1.124) получим (1.125):
i – это значит, что в производных под знаком суммирования сохраняются постоянными числа молей всех компонентов, кроме i-го. Можно показать, что первые две производные в скобах уравнения (1.124) соответственно равны – S и V. Поэтому вместо (1.124) получим (1.125):
k
dG = – SdT + Vdp + μidni , (1.125)
i=1
где величина
μi = (G/ni)T,p,
называется химическим потенциалом i-го компонента.
Химический потенциал i-го компонента равен приращению энергии Гиббса при добавлении одного моля этого компонента к большому объему системы при постоянных температуре и давлении и неизменных количествах других компонентов. Система должна быть достаточно большой, чтобы от добавления одного моля вещества i ее состав практически не изменился. Химический потенциал чистого вещества равен энергии Гиббса одного моля данного вещества:
 (1.126)
(1.126)
При постоянных р и Т вместо (1.125) получим (1.127):
k
dGp,T = (idni)p,T . (1.127)
i=1
Химический потенциал данного компонента в системе зависит как от его концентрации, так и от вида и концентрации других компонентов системы. Только в случае смеси идеальных газов химический потенциал данного компонента (i) зависит лишь от его концентрации и температуры:
i i RT ln (pi /р),
где pi - парциальное давление в атмосферах компонента i в смеси, i – стандартный химический потенциал компонента i при Т =298 К и р =1атм. Это уравнение обычно записывают в виде:
i i RT lnрi . (1.128)
Однако следует помнить, что в (1.128) рi фактически заменяет величину pi /рi, которая не имеет размерности и поэтому только от нее может быть взят логарифм.
В случае идеального раствора зависимость химического потенциала i-го компонента от его мольной доли в растворе хi и температуры выражается уравнением:
i i RT lnхi , (1.129)
где i – химический потенциал чистого i-го компонента (при х
i = 1).
Химический потенциал характеризует способность рассматриваемого компонента к выходу из данной фазы путем испарения, растворения, кристаллизации, химического взаимодействия и т.д. При этом переход компонента происходит самопроизвольно из данной фазы (например,(1)), в которой его химический потенциал i(1) больше, в фазу (2), в которой его химический потенциал i(2) меньше. Такой переход сопровождается уменьшением химического потенциала этого компонента в фазе (1) и увеличением его в фазе (2). Если в результате установится равновесие, то химический потенциал окажется одинаковым в обеих фазах ('i(1) = 'i(2)).
ЛЕКЦИЯ 7 1.3.11. Константы равновесия
Химическое равновесие означает неизменность во времени параметров системы. Рассмотрим в общем виде химическую реакцию в газовой фазе, считая газ идеальным (при низких р):
аА + вВ ⇄ сС+dD .
Это равновесие при постоянной температуре характеризуется константой равновесия Кр:
Кр = рс(С)pd(D)/ ра(А) рв(В), (1.130)
где р(i) – парциальные давления компонентов системы. В случае аналогичного химического равновесия в идеальном растворе константа равновесия имеет следующее выражение:
Кс = сс(С)cd(D)/ са(А) св(В), (1.131)
где с(i) – молярные концентрации компонентов в растворе. Уравнения (1.130) и (1.131) представляют собой выражение закона действующих масс применительно к идеальным газам и разбавленным растворам, установленного эмпирически норвежскими учеными К. Гульдбергом и П. Вааге. В настоящее время уравнения (1.130) и (1.131) выведены теоретически.
Если равновесные системы содержат индивидуальные вещества в конденсированных фазах, то их концентрации и парциальные давления являются постоянными и не входят в правые части (1.130) или (1.131), а учитываются соответствующими значениями констант равновесий.
Если равновесная газообразная система не является идеальной, то в (1.130) вместо каждого давления вводят величину, которая называется фугитивностью или летучестью:
f = p ,
где - безразмерный коэффициент фугитивности, зависящий от р и Т. Фугитивность имеет такую же размерность, как и давление. Фугитивность - это такое давление реального газа, при котором газ можно описать по (1.128) и (1.130) как идеальный. Применение
f практикуется вместо парциальных давлений при высоких давлениях и низких температурах (до 1 МПа ).
Для перехода от реальных растворов к идеальным введено понятие активности (а):
а = с с,
где с - коэффициент активности, зависящий от Т и с. Активность - это такая кажущаяся концентрация, при использовании значения которой реальные растворы можно описать по (1.129) и (1.131). При разбавлении раствора с стремится к единице, и активность становится равной концентрации.
Связь между константами равновесия для рассмотренной реакции, выраженными через концентрации и активности определяется соотношением:
Ка = Кс ( сс (С)γ (D)/ са (А) св (В)) . (1.132)
(D)/ са (А) св (В)) . (1.132)
1.3.12. Равновесия в газовых реакциях и
изотерма химической реакции
Показано, что если реакция протекает в равновесной системе, независимо от ее состава, включающего газы, жидкости, твердые вещества или растворы, то выполняется следующее условие химического равновесия:
 i i = 0,
i i = 0,
где i– стехиометрические коэффициенты уравнения химической реакции, i – значения химических потенциалов компонентов, соответствующие равновесному состоянию (ΔGp,T = 0). Если равновесное состояние не достигнуто, то выполняется уравнение:
ΔGp,T = i i.
i i.
Рассмотрим в качестве примера реакцию аА + вВ ⇄сС + dD, протекающую при постоянных давлении и температуре в смеси идеальных газов с начальными неравновесными парциальными давлениями р'(А), р'(В), р'(С), р'(D). В этом случае химический потенциал каждого компонента можно представить по (1.128) следующим образом:
i = RT ln рi .
Тогда:
G = c(C) + d(D) a (A) - b(B) = c(C) + d(D)
a (A) b(B) + RT(cln р(C) + dln р(D) – aln р(A) –bln р(B))
или
G = G + RTln . (1.133)
. (1.133)
Полученное выражение называется изотермой химической реакции или изотермой Вант-Гоффа. В состоянии равновесия закон действующих масс для данной реакции может быть представлен в следующем виде:
Содержание третьего закона более глубоко раскрывается с помощью статистической теории и представлений квантовой теории строения вещества. В 1872 году австрийский физик Больцман первым пришел к заключению о том, что энтропия является функцией только термодинамической вероятности (или мультиплетности) W и что это соотношение должно быть логарифмическим:
S = k lnW, (1.121)
где k – постоянная Больцмана (k = R/NA). Мультиплетность W равна числу различных способов размещения структурных частиц системы (или вещества) при нахождении ее при данных термодинамических параметрах. В качестве наглядного представления о величине W рассмотрим схему двумерного кристалла (рис.1.14).




а) б)
Р

 ис.1.14. Схемы двумерных кристаллов из атомов А и В (а) и только из атомов А (б): – атомы А; – атомы В
ис.1.14. Схемы двумерных кристаллов из атомов А и В (а) и только из атомов А (б): – атомы А; – атомы ВДопустим, что в узлах кристалла находятся атомы одного и того же элемента – изотопы А и В (а). Энергия взаимодействия между ними одинакова, поэтому независимо от того, в каких узлах и какие атомы находятся, энергия и состояние кристалла при одних и тех же р и Т будут одинаковыми. Допустим также, что при некотором значении Т атомы А и В могут перескакивать вследствие диффузии из одного узла в другой. Вычислим, сколькими способами можно реализовать данное состояние. Очевидно, что два состояния кристалла будут при размещении атомов В по диагоналям кристалла и четыре состояния кристалла будут при размещении атомов В вдоль каждой из сторон кристалла. Всего шесть состояний – это и есть величина
W. Значение энтропии такого кристалла будет равно S=1,381·10-23 Дж/К ln6 = 2,47 ·10-23 Дж/К. Если бы рассматриваемый кристалл состоял только из атомов А (б), то при абсолютном нуле температуры в этом случае возможно было бы только одно состояние – когда атомы А находятся в узлах кристаллической решетки, то есть W=1. Тогда по формуле (1.121) энтропия равна нулю
S = k ln1 = 0,
что находится в соответствии с третьим законом термодинамики.
Абсолютную энтропию газа при температуре Т можно вычислить, интегрируя dqобр/Т от 0 К до заданной температуры. Если известны теплоемкости, энтальпия плавления в точке плавления Тпл и энтальпия испарения в точке кипения Ткип, то абсолютная энтропия при температуре Т может быть рассчитана по уравнению (1.122):
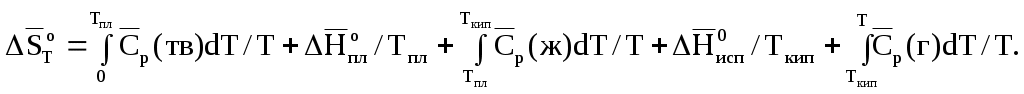 (1.122)
(1.122)Если твердое тело находится в разных модификациях и их взаимное превращение сопровождается изменением энтальпии, то в сумму (1.121) нужно включить соответствующие энтропии фазовых превращений. Четвертое слагаемое (1.122) представляет собой мольную энтропию испарения. В стандартных условиях в точках кипения для многих жидкостей она постоянна и равна примерно 88кДж/(моль К):
Это уравнение, известное как правило Трутона, полезно для оценки мольной теплоты испарения жидкостей с известными точками кипения.
1.3.10. Химический потенциал
В случае открытых систем в них могут вводиться или из них могут выводиться какие-то вещества. В частности, при протекании химических реакций изменяются числа молей компонентов в системах. В таких случаях энергия Гиббса каждой системы зависит не только от р и Т, но и от количеств веществ, а ее полный дифференциал через частные производные имеет следующий вид:
k
dG = (G/T)
dni , (1.124)
i=1
где k – число различных веществ; n1, n2, n3 … nk – числа молей веществ; ni – число молей вещества i; j
k
dG = – SdT + Vdp + μidni , (1.125)
i=1
где величина
μi = (G/ni)T,p,
называется химическим потенциалом i-го компонента.
Химический потенциал i-го компонента равен приращению энергии Гиббса при добавлении одного моля этого компонента к большому объему системы при постоянных температуре и давлении и неизменных количествах других компонентов. Система должна быть достаточно большой, чтобы от добавления одного моля вещества i ее состав практически не изменился. Химический потенциал чистого вещества равен энергии Гиббса одного моля данного вещества:
При постоянных р и Т вместо (1.125) получим (1.127):
k
dGp,T = (idni)p,T . (1.127)
i=1
Химический потенциал данного компонента в системе зависит как от его концентрации, так и от вида и концентрации других компонентов системы. Только в случае смеси идеальных газов химический потенциал данного компонента (i) зависит лишь от его концентрации и температуры:
i i RT ln (pi /р),
где pi - парциальное давление в атмосферах компонента i в смеси, i – стандартный химический потенциал компонента i при Т =298 К и р =1атм. Это уравнение обычно записывают в виде:
i i RT lnрi . (1.128)
Однако следует помнить, что в (1.128) рi фактически заменяет величину pi /рi, которая не имеет размерности и поэтому только от нее может быть взят логарифм.
В случае идеального раствора зависимость химического потенциала i-го компонента от его мольной доли в растворе хi и температуры выражается уравнением:
i i RT lnхi , (1.129)
где i – химический потенциал чистого i-го компонента (при х
i = 1).
Химический потенциал характеризует способность рассматриваемого компонента к выходу из данной фазы путем испарения, растворения, кристаллизации, химического взаимодействия и т.д. При этом переход компонента происходит самопроизвольно из данной фазы (например,(1)), в которой его химический потенциал i(1) больше, в фазу (2), в которой его химический потенциал i(2) меньше. Такой переход сопровождается уменьшением химического потенциала этого компонента в фазе (1) и увеличением его в фазе (2). Если в результате установится равновесие, то химический потенциал окажется одинаковым в обеих фазах ('i(1) = 'i(2)).
ЛЕКЦИЯ 7 1.3.11. Константы равновесия
Химическое равновесие означает неизменность во времени параметров системы. Рассмотрим в общем виде химическую реакцию в газовой фазе, считая газ идеальным (при низких р):
аА + вВ ⇄ сС+dD .
Это равновесие при постоянной температуре характеризуется константой равновесия Кр:
Кр = рс(С)pd(D)/ ра(А) рв(В), (1.130)
где р(i) – парциальные давления компонентов системы. В случае аналогичного химического равновесия в идеальном растворе константа равновесия имеет следующее выражение:
Кс = сс(С)cd(D)/ са(А) св(В), (1.131)
где с(i) – молярные концентрации компонентов в растворе. Уравнения (1.130) и (1.131) представляют собой выражение закона действующих масс применительно к идеальным газам и разбавленным растворам, установленного эмпирически норвежскими учеными К. Гульдбергом и П. Вааге. В настоящее время уравнения (1.130) и (1.131) выведены теоретически.
Если равновесные системы содержат индивидуальные вещества в конденсированных фазах, то их концентрации и парциальные давления являются постоянными и не входят в правые части (1.130) или (1.131), а учитываются соответствующими значениями констант равновесий.
Если равновесная газообразная система не является идеальной, то в (1.130) вместо каждого давления вводят величину, которая называется фугитивностью или летучестью:
f = p ,
где - безразмерный коэффициент фугитивности, зависящий от р и Т. Фугитивность имеет такую же размерность, как и давление. Фугитивность - это такое давление реального газа, при котором газ можно описать по (1.128) и (1.130) как идеальный. Применение
f практикуется вместо парциальных давлений при высоких давлениях и низких температурах (до 1 МПа ).
Для перехода от реальных растворов к идеальным введено понятие активности (а):
а = с с,
где с - коэффициент активности, зависящий от Т и с. Активность - это такая кажущаяся концентрация, при использовании значения которой реальные растворы можно описать по (1.129) и (1.131). При разбавлении раствора с стремится к единице, и активность становится равной концентрации.
Связь между константами равновесия для рассмотренной реакции, выраженными через концентрации и активности определяется соотношением:
Ка = Кс ( сс (С)γ
1.3.12. Равновесия в газовых реакциях и
изотерма химической реакции
Показано, что если реакция протекает в равновесной системе, независимо от ее состава, включающего газы, жидкости, твердые вещества или растворы, то выполняется следующее условие химического равновесия:
где i– стехиометрические коэффициенты уравнения химической реакции, i – значения химических потенциалов компонентов, соответствующие равновесному состоянию (ΔGp,T = 0). Если равновесное состояние не достигнуто, то выполняется уравнение:
ΔGp,T =
Рассмотрим в качестве примера реакцию аА + вВ ⇄сС + dD, протекающую при постоянных давлении и температуре в смеси идеальных газов с начальными неравновесными парциальными давлениями р'(А), р'(В), р'(С), р'(D). В этом случае химический потенциал каждого компонента можно представить по (1.128) следующим образом:
i = RT ln рi .
Тогда:
G = c(C) + d(D) a (A) - b(B) = c(C) + d(D)
a (A) b(B) + RT(cln р(C) + dln р(D) – aln р(A) –bln р(B))
или
G = G + RTln
 . (1.133)
. (1.133)Полученное выражение называется изотермой химической реакции или изотермой Вант-Гоффа. В состоянии равновесия закон действующих масс для данной реакции может быть представлен в следующем виде: