Файл: Лекция 1 Тема Химическая термодинамика.doc

0). Как правило, это сопровождается увеличением объема (  0). Поэтому наклон кривых ОА, ОВ, ОС практически всегда положителен. Для процессов сублимации и испарения . Объем пара можно выразить величинами параметров уравнения состояния идеального газа: =RT/p. Тогда dp/dT =  . Разделив переменные последнего уравнения и проинтегрировав его при допущении, что в узком интервале температур испарения (и сублимации) является постоянной величиной, получим следующее выражение:


ln p = (- H_ф/RT_ф ) + const . (2.2)

Э

4

т.кип.(станд.)

3

2 жидк. фаза тв. фаза

1
0

-0,5

2 3 4 10³/Т
то уравнение линейной зависимости ln p от 1/Т, что и подтверждается экспериментальными данными как для испарения, так и для возгонки (например, рис.2.2 для воды).

---

Рис.2.2. Зависимость логарифма давления пара воды от значений (1/Т)∙10³, соответствующая преобразованному (2.2) в уравнение:

Константа интегрирования в (2.2) равна первому слагаемому при р = 1 атм. По этому уравнению кривые, например, ОА и ОС рис.2.1 могут быть построены на основании известных данных о теплотах сублимации и испарения. И наоборот, по графикам ln p = f(1/T) можно определить теплоты фазовых переходов (по тангенсам углов наклона прямых: и положение тройной точки, в которой давление насыщенного пара вещества над жидкой и твердой фазой равны между собой. Поскольку в процессе плавления объем системы изменяется незначительно, то в соответствии с (2.1) угол наклона кривой ОВ существенно больше, чем у кривых ОА и ОС. Для некоторых веществ (чугуна, воды) кривая ОВ имеет наклон влево. Подобное явление объясняется большей плотностью жидких фаз по сравнению с плотностью твердых фаз, т.е. при повышении температуры  0, но  0, и градиент dp/dT отрицателен.

Если вещество в твердом состоянии может существовать в нескольких полиморфных модификациях, то его диаграмма состояния усложняется. Рассмотрим это на примере серы, которая имеет две твердые кристаллические модификации: ромбическую S(ром) и моноклинную S(м) (диаграмма рис. 2.3).




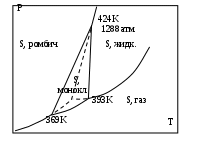
Рис. 2.3. Диаграмма состояния серы

На диаграмме видны три тройные точки, соответствующие равновесиям в трехфазных состояниях. Видно также как вещество может существовать в нескольких кристаллических формах, и при этом имеется температура перехода, выше которой устойчивой является одна модификация, а ниже - вторая. Если при температуре перехода превращение модификаций самопроизвольно протекает как в прямом, так и в обратном направлениях, то такой переход называется энантиотропным, например, как в случае серы. В некоторых случаях переход осуществляется только при изменении температуры в одном направлении. Такой переход встречается реже и называется монотропным. Примером является переход белого фосфора в красный.

---

2.3. ФАЗОВЫЕ РАВНОВЕСИЯ В ДВУХКОМПОНЕНТНЫХ СИСТЕМАХ

Фазовая диаграмма для двухкомпонентной системы в общем случае будет трехмерной, т.к. могут изменяться: давление, температура, состав. Для жидкостей и твердых тел давление можно исключить из числа переменных, тогда С+Ф = К+n = 2+1 = 3, а наибольшее число фаз в системе равно трем; диаграмма состояния будет двумерной в координатах "Т - состав".

ЛЕКЦИЯ 8 2.3.1. Равновесие кристаллы - жидкость

Рассмотрим вначале систему, компоненты которой не образуют друг с другом химических соединений, неограниченно растворимы друг в друге в случае жидкого состояния одного из компонентов, но нерастворимы друг в друге в твердых состояниях. Например, систему: вода – соль (рис.2.4). Чистая вода в виде льда плавится при 273,15 К. Введение в воду растворяющегося вещества повышает ее энтропию и понижает ее химический потенциал (действительно, по (1.23) , а с другой стороны, G = H-TS). Химические потенциалы твердых компонентов остаются постоянными, т.к. твердых растворов не образуется. Поэтому выравнивание химических потенциалов компонентов в жидких и твердых фазах в точках равновесия достигается при более низких температурах, чем температуры кристаллизации компонентов. При этом две кривые кристаллизации пересекаются в некоторой точке, соответствующей минимальной температуре затвердевания. Смесь, состав которой соответствует минимальной температуре затвердевания, называется эвтектической или эвтектикой (от греческого слова "эвтектос" - хорошо плавящийся), а сама температура - эвтектической температурой.

(I) (II)

Т, К Т

К

• а' А • а

М L

---

273 • б΄ N • б

В C

Е с' F с • •d

х' • Д • х

Н₂О массовые доли соль время охлаждения

Рис. 2.4. Диаграмма состояния (I) и кривая охлаждения (II)

с постоянной скоростью системы вода – соль

В фазовом поле А, соответствующем жидкому раствору соли в воде, имеются две степени свободы, т.е. можно одновременно изменять и состав, и температуру. Следовательно, при охлаждении раствора его состав не изменяется (например, состав раствора в точке а'). При некоторой температуре кривая охлаждения (II) достигает точки б, которой на диаграмме соответствует точка б' пересечения прямой а'х' с кривой кристаллизации воды (или плавления льда при нагревании), называемой линией ликвидуса (от латинского слова "ликвидус" – жидкий). В этой точке начинают выпадать кристаллы льда. Теплота кристаллизации воды при этом компенсирует частично потерю системой теплоты охлаждения, и кривая охлаждения понижает свой наклон (бс). Указанному участку кривой охлаждения соответствует отрезок линии ликвидуса б΄с΄, вдоль которого в каждой точке сохраняются равновесные состояния системы с одной степенью свободы и двумя фазами – жидкой и твердой. При этом твердая фаза – это лед, а состав раствора изменяется в соответствии с кривой ликвидуса. В точке с΄ начинает кристаллизоваться соль и одновременно находятся в равновесии три фазы: раствор, лед и соль (эвтектика). При дальнейшем охлаждении системы кристаллизуются вода и соль при неизменной температуре и постоянном составе раствора, число степеней свободы равно нулю (горизонтальный участок кривой охлаждения cd). Кривая, ниже которой существуют только твердые фазы, называется кривой солидуса (от латинского "солидус" - твердый). В данном случае это прямая EF, параллельная оси состава.

Эвтектика представляет собой смесь мельчайших кристалликов воды и соли. Характерным является то, что эвтектика всегда обогащена более легкоплавким компонентом. Сходство эвтектики и чистого компонента состоит в том, что они кристаллизуются при постоянной температуре. Однако при изменении давления у эвтектики изменяется не только температура плавления, но и состав. Кроме того при кристаллизации чистого компонента состав твердой и жидкой фаз одинаков, а при кристаллизации эвтектики состав жидкой фазы отличается от состава каждой из равновесной с ним твердых фаз.

---

Рассматриваемая диаграмма состояния системы вода – соль имеет также фазовое поле В, в котором система содержит частицы льда и жидкий раствор соли в воде. В фазовом поле С система содержит твердые частицы соли и жидкий раствор соли в воде. В фазовом поле Д система состоит только из твердых частиц соли и льда. Линии ликвидуса и солидуса соответствуют равновесным состояниям твердых фаз и жидких растворов. Фазовый состав системы в любой точке полей В и С диаграммы можно определить, проведя через эту точку прямую, параллельную оси абсцисс, до пересечения ее с линией ликвидуса и одной из ординат. При этом на состав твердой фазы укажет ордината, а состав раствора будет соответствовать точке пересечения параллельной прямой с линией ликвидуса.

Количества обеих фаз можно определить по правилу рычага: они соотносятся между собой так же, как длины отрезков, на которые рассматриваемая точка диаграммы делит прямую, параллельную оси абсцисс (длины противоположных плечей рычага).

Например, если при охлаждении раствора, состав которого соответствовал точке К, система пришла в точку N, то параллельная оси состава пунктирная прямая ML точками М и L укажет на ее фазовый состав: М – раствора, L – твердой фазы – соли. При этом масса раствора будет так относиться к массе твердой фазы, как длина отрезка NL относится к длине отрезка MN.

Аналогично диаграмме состояния системы вода – соль выглядят диаграммы состояния металл – металл при условии их растворимости в жидком состоянии (в расплавах) и нерастворимости в твердом состоянии. Например, на рис.2.5 представлены кривые охлаждения и диаграмма состояния системы кадмий – висмут. Видно, что когда охлаждается жидкость, состоящая из одного компонента, график зависимости температуры от времени имеет почти постоянный наклон. Однако при температуре кристаллизации кривая охлаждения переходит в горизонтальную прямую линию, если охлаждение производится достаточно медленно. Остановка на кривой охлаждения является результатом выделения теплоты в процессе затвердевания жидкости. Когда охлаждается раствор, то при температуре начала кристаллизации одного из компонентов наклон кривой уменьшается, что обусловлено выделением теплоты при постепенной кристаллизации твердого вещества по мере охлаждения раствора, а также изменением теплоемкости системы. Такие изменения наклона (точки перегиба) видны на кривых охлаждения сплавов, содержащих 0,2 и 0,8 кадмия. Кривые имеют и горизонтальные участки – в обоих случаях при 140

---