Файл: Инструкция по регистрации на портале дистанционного образования moodle 3.docx

Вариант 15.

Задача 1. Время восстановления ЧСС после пробежки, сек

анемия	220	240	180	120	200	190	210	180	180	185	165
контр. гр.	105	146	180	300	120	180	260	120	120	180	260

Задача 2. Влияние операции на объем циркулирующей плазмы , мл\кг

до операции	43	36	37	36	30	26	44	30	40	31
после операции	43	33	44	34	40	31	26	33	36	37

---

Практическое занятие 5. Непараметрические критерии проверки статистических гипотез.

Для проверки статистических гипотез может применяться целый ряд непараметрических критериев, среди которых важное место занимают так называемые ранговые критерии. Применение этих критериев основано на ранжировании членов сравниваемых групп. При этом сравниваются не сами члены ранжированного ряда, а их порядковые номера или ранги.

СЛУЧАЙ 1. Выборки независимы.

Используется U-критерий Манна—Уитни для проверки гипотезы о принадлежности сравниваемых независимых выборок к одной и той же генеральной совокупности. Для его вычисления:

• 
  Объединим все значения обеих выборок в один ранжированный ряд
  
• 
  Каждому элементу этого ряда присвоим ранг, при этом если несколько элементов ряда совпадают по величине, то каждому присваивается ранг, равный среднему арифметическому их номеров
  
• 
  Для каждой выборки находятся суммы рангов R
  
• 
  Далее рассчитываются статистики:
  

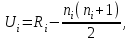где i = 1 и 2 – номер выборки

• 
  В качестве тестовой статистики выбирают минимальную величину U и сравнивают ее с табличным значением для принятого уровня значимости и объемов выборок n₁, n₂.
  
• 
  Если U_выч > U_крит то Н(0)
  
• 
  Если U_выч ≤ U_крит то Н(1)
  

Работа с преподавателем

Пример. Проверим гипотезу о принадлежности сравниваемых независимых выборок к одной и той же генеральной совокупности с помощью непараметрического U-критерия.
Содержание вещества В в крови, моль\л

1 группа	8	8	9	10	7	7	9	9	11	6
2 группа	8	9	9	11	12	12	13	13	12	11

---

Н0:

номер

1 гр

2 гр

ранг

---

Отдельно для каждой выборки рассчитываем суммы рангов их вариант R1 и R2. В нашем случае:

Статистика U₁ = , U₂=

Вывод:

	R1	R2	Uвыч-М-У	p-уровень	n1	n2
Вещество В

СЛУЧАЙ 2. Выборки зависимые

В случае попарно связанных выборок применяется Т-критерий Уилкоксона. При этом:

• 
  Вычисляются попарные разницы значений до и после
  
• 
  Попарные разницы, кроме нулевых, без учета знака ранжируются в один ряд
  
• 
  Разницам, кроме нулевых, присваиваются ранги, при чем одинаковым по модулю величинам присваивают одинаковый ранг
  
• 
  Отдельно вычисляют сумму рангов положительных (Т+) и отрицательных разностей (Т-),
  
• 
  Меньшую из двух таких сумм без учета знака выбирают в качестве критерия
  
• 
  Если Т_выч > Т_крит то Н(0)
  
• 
  Если Т_выч ≤ Т_крит то Н(1)
  

Работа с преподавателем

Стояла задача определить влияет ли препарат «Биоконт» на содержание белка в плазме крови. С этой целью препарат был испытан на десяти кроликах. Результаты эксперимента приведены в таблице.
Выдвигаем нулевую гипотезу:

до	2,4	3,7	4,2	2,8	3,3	4,5	3,9	2,7	4,4	3
после	3	3,5	5	3	4,9	4,4	3,6	2,5	3	4,1
разница
ранжир
ранги
Т+
Т-

---

В качестве критерия выбираем меньшее значение Т_выч =

Табличное значение для уровня значимости 0,05 и числа пар наблюдений п= (двусторонний критерий):

Т_крит =

Вывод:

	Твыч-Уилкоксона	p-уровень	n
Концентрация белка

Контрольные вопросы

1. 
   Основные задачи биостатистики
   
2. 
   Генеральная совокупность и выборка. Какие бывают выборки.
   
3. 
   Понятие распределения, нормальное распределение и его свойства
   
4. 
   В каком случае две совокупности считаются не отличающимися по данному признаку
   
5. 
   Понятие статистических гипотез
   
6. 
   Как проверяются гипотезы
   
7. 
   Уровень значимости и достигнутый уровень значимости
   
8. 
   Виды критериев, как выбрать критерий
   

Контрольное задание:

В контрольных задачах к Практическому занятию 4 проверить гипотезу о принадлежности двух выборок одной генеральной совокупности с использованием непараметрических критериев. Обосновать выбор критерия. Сформулировать нулевую и альтернативную гипотезы. Сделать выводы на уровне значимости =0,01 или =0,05

---