Файл: Инструкция по регистрации на портале дистанционного образования moodle 3.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 364
Скачиваний: 1
СОДЕРЖАНИЕ
Инструкция по регистрации на портале дистанционного образования MOODLE
КРЕДИТ 1. ВЫБОРОЧНЫЙ МЕТОД В НАУЧНЫХ ИССЛЕДОВАНИЯХ
РАЗДЕЛ 1. ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Практическое занятие 1: Построение и описание гистограмм
Практическое занятие 2. Вычисление статистических характеристик случайных величин
Практическое занятие 3. Проверка гипотезы о нормальности распределения случайной величины.
Задание к теме: Проверка гипотезы о нормальности распределения случайной величины.
РАЗДЕЛ 2. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Практическое занятие 4. Критерий Стьюдента для анализа биомедицинских данных.
Практическое занятие 5. Непараметрические критерии проверки статистических гипотез.
Практическое занятие 6. Сравнение относительных величин
РАЗДЕЛ 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ
Практические занятие 7. Таблицы сопряженности
Практическое занятие 8. Линейная корреляция.
Практическое занятие 9. Прогнозирование на основе линейной регрессии
Практическое занятие 10. Метод однофакторного дисперсионного анализа.
Критические значения коэффициента асимметрии As
Критические значения коэффициента эксцесса Ех
Критические точки двустороннего t-критерия Стьюдента
Алгоритм подбора критериев при сравнении двух выборок
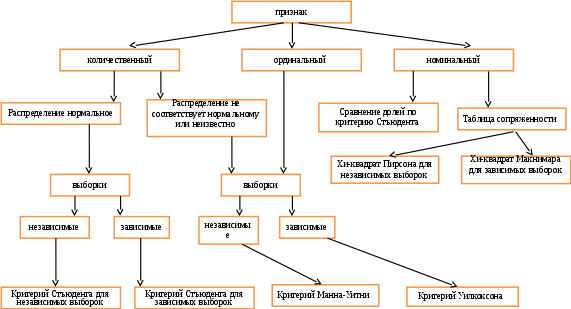
РАЗДЕЛ 2. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Практическое занятие 4. Критерий Стьюдента для анализа биомедицинских данных.
Наиболее распространенным параметрическим критерием оценки различий между сравниваемыми генеральными средними значениями является критерий Стьюдента, или t-критерий. Нулевая гипотеза заключается в равенстве генеральных средних или, другими словами, проверяется нулевая гипотеза о принадлежности двух сравниваемых выборок одной и той же генеральной совокупности.
Работа с преподавателем
СЛУЧАЙ 1. Выборки независимы.
Проверяемый t-критерий вычисляется по формуле
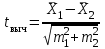
где m1, m2 — стандартные ошибки средних значений сравниваемых выборок.
tкрит находится по таблице для заданного α и числа степеней свободы
f =n1 + n2 – 2
Если │tвыч │< tкрит то Н(0)
Если │ tвыч│≥ tкрит то Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями на соответствующем уровне значимости.
Работа с преподавателем.
Задача. В группе здоровых людей и больных гепатитом было определено содержание белка в сыворотке крови (Таблица 1). Определить, отличаются ли средние значения белка в двух генеральных совокупностях, если известно, что белок распределен по нормальному закону и генеральные дисперсии обеих совокупностей равны.
Таблица 1.
| X1 (норма) | 6,85 | 6,51 | 6,9 | 7,04 | 5 | |
| X2 (гепатит) | 7,28 | 8,9 | 6,52 | 8,15 | 7,53 | 8,12 |
Решение:
Н(0):
Н(1):
Вычислим средние значения для двух выборок:
Для следующих вычислений составим таблицу
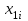 | 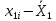 | 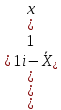 | 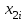 | 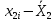 | 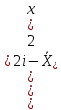 |
| 6,85 | | | 7,28 | | |
| 6,51 | | | 8,9 | | |
| 6,9 | | | 6,52 | | |
| 7,04 | | | 8,15 | | |
| 5 | | | 7,53 | | |
| | | | 8,12 | | |
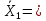 | | 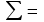 | 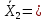 | | 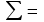 |
Вычислим среднее квадратическое отклонение для выборок:
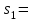
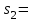
Найдем стандартные ошибки:
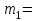
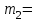
Рассчитаем t-критерий:
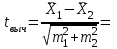
Определим число степеней свободы в двух группах: f = (n+n2-2)=
Определим по таблице двусторонний критерийtкрит для α=0,05
tкрит=
Вывод:
Сведем результаты расчетов в таблицу и представим графически
| группа | n |  (г/л) (г/л) | s (г/л) | t-выч | t-критич | р-уровень |
| норма | | | | | | |
| гепатит | | | |
СЛУЧАЙ 2. Выборки зависимы.
Для сравнения двух зависимых выборок или выборок с попарно связанными вариантами проверяют гипотезу о равенстве нулю среднего значения их попарных разностей.
При подобных исследованиях все наблюдения можно представить в виде n-пар измерений (например, до и после)
Для каждой пары вычисляется разность di, i=1, n
Для полученного ряда вычисляется среднее
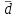 и среднеквадратичное отклонение
и среднеквадратичное отклонение 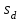 , стандартную ошибку средней
, стандартную ошибку средней 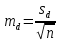
Критерий Стъюдента определяется по формуле
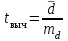
tкрит находится по таблице для заданного α и числа степеней свободы f =n-1
Если │tвыч │< tкрит то Н(0)
Если │ tвыч│≥ tкрит то Н(1) и делается заключение о наличии статистически значимых различий между средними значениями «до» и «после» на соответствующем уровне значимости.
Работа с преподавателем. В группе из 6 больных гипертонией изучалось влияние лекарственного препарата, снижающего артериальное давление. В результате опыта получилось 2 вариационных ряда систолического давления: первый – до приема препарата, второй – после приема:
Таблица 1.
| До приема | 250 | 240 | 210 | 190 | 185 | 170 |
| После приема | 210 | 195 | 165 | 170 | 155 | 175 |
Определить, изменяется ли в генеральной совокупности систолическое артериальное давление после приема препарата и насколько статистически значимы полученные результаты, если известно,что данные имеют нормальное распределение и две генеральные дисперсии равны?
Для наглядности представим данные в следующей таблице:
Таблица 2.
| xki (до приема) | хoi (после приема) | di (разница давлений) |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| Ср. знач.= | Ср. знач.= | Ср. знач.= |
Н(0):
Н(1):
Для разностей давлений:
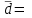
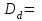
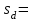
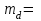
Определим tвыч:
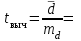
Определим по таблице Стьюдента tкрит для α=0,05 и числа степеней свободы f=n-1=
tкрит= (двусторонний критерий).
Вывод:
Сведем результаты расчетов в таблицу
| группа | n |  (мм.рт.ст.) (мм.рт.ст.) |  (мм.рт.ст.) (мм.рт.ст.) | sd (мм.рт.ст.) | t-выч. | t-критич. | р-уровень |
| до приема | | | | | | | |
| после приема | |