Файл: Инструкция по регистрации на портале дистанционного образования moodle 3.docx

РАЗДЕЛ 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ

Практические занятие 7. Таблицы сопряженности

Существует множество признаков, различных явлений и вещей, измерение которых затруднено или вовсе невозможно. Например, как измерить признак «профессия» или «вид патологии», а как сравнить эти признаки для получения статистического представления о профессиональной заболеваемости?

В этих случаях изучается распространенность признаков, частота встречаемости признаков (доля объектов с интересующим нас признаком) в различных выборках, оценивается взаимосвязь частоты встречаемости одного признака с частотой встречаемости другого признака.

Для этого используются таблицы сопряженности. Столбцы этой таблицы обозначают градации одного признака, строки – градации другого признака. В каждой ячейке записывается число случаев с сопряженными признаками.

Наиболее простой случай таблица 2х2 (исследуется частота совместного распространения двух признака, каждый из которых имеет две градации).

В общем случае Н(0) формулируется следующим образом:

• 
  в генеральных совокупностях доля объектов с интересующими нас признаками одинакова
  
• 
  или частота встречаемости одного признака не зависит от частоты встречаемости другого признака
  
• 
  или какой-либо фактор не влияет на частоту встречаемости признака (признаков)
  

СЛУЧАЙ 1. Выборки независимые

Предположим, что у нас есть два качественных признака, характеризующие обследованных лиц. Занесем эти данные в таблицу сопряженности

	Первая признак (первая градация)	Первый признак (вторая градация)	Всего
Второй признак (первая градация)	Частота встречаемости a	Частота встречаемости b	a +b
Второй признак (вторая градация)	Частота встречаемости c	Частота встречаемости d	с+d
	n1=a+c	n2=b+d	n =a+b+c+d

---

Критерием для проверки нулевой гипотезы является хи-квадрат Пирсона с поправкой Йетса





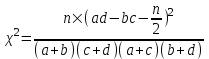
Его критическое значение находится для заданного уровня значимости α и числа степеней свободы f=(m-1)(n-1), где m-число столбцов, n – число строк (Приложение 5).

Если 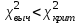то Н(0) принимается,

В случае 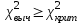принимается Н(1)

Можно вычислить меру связи между двумя признаками – ею является коэффициент ассоциации Юла Q(аналог коэффициента корреляции)

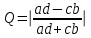
Qлежит в пределах от 0 до 1. Близкий к единице коэффициент свидетельствует о сильной связи между признаками. При равенстве его нулю – связь отсутствует.
Работа с преподавателем

Руководствуясь тем, что аспирин препятствует образованию тромбов, Г. Харатер решил проверить, нельзя ли снизить риск тромбоза назначением небольших доз аспирина (160 мг/сут.). Было проведено контролируемое испытание. Все больные, согласившиеся принять участие в испытании и не имевшие противопоказаний к аспирину, были случайным образом разделены на две группы: 1-я получала плацебо, 2-я - аспирин. Исследование проводилось до тех пор, пока общее число больных с тромбозом шунта не достигло 24. Группы практически не различались по возрасту, полу и продолжительности лечения гемодиализом. В 1-й группе тромбоз шунта произошел у 18 из 25 больных, во 2-й -у 6 из 19. Можно ли говорить о статистически значимом различии доли больных тромбозом, а тем самым об эффективности аспирина?

Зададим уровень значимости α=0,05

Сформулируем Н(0): в генеральной совокупности доля больных тромбозом не зависит от приема аспирина.

Занесем результаты испытания в таблицу.

	Тромбоз есть	Тромбоза нет
Плацебо	18	7	25
Аспирин	6	13	19
Всего	24	20	44

---

Посчитаем значение критерия хи-квадрат с поправкой Йетса



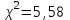
Q=0,7

Мы задали 5% -ный уровень значимости α = 0,05 . Тогда критическое значение = 3,84 (по таблице для f=1). Полученное значение χ²=5,56 больше, чем критическое, следовательно, мы отвергаем Н(0) гипотезу о том, что аспирин не влияет на проявление тромбоза шунта. Следовательно, мы можем утверждать с вероятностью 95%, что использование аспирина эффективно снижает риск тромбоза в генеральной совокупности.

Q=0,7 показывает сильную связь между приемом аспирина и вероятностью тромбоза.
Случай 2. Выборки зависимые

Над одними и теми же объектами проводятся два наблюдения: до и после. (прием лекарства, обучение, внушение и т.д.)

Подсчитывается сколько раз данное свойство встречается:

• 
  и «до» и «после», (+,+)
  
• 
  только «до» (+,-)
  
• 
  только «после» (-,+)
  
• 
  ни «до» ни «после» (-,-)
  

	Наличие признака «после»
Наличие признака «до»	нет (-)	есть (+)
есть (+)	a Число изменений от (+) к (-)	c Число сохранивших (+)
нет (-)	b Число сохранивших (-)	d Число изменений от (–) к (+)

• 
  Н(0) – доля объектов с интересующим нас признаком «после» не изменилась по сравнению с «до»
  
• 
  Вычисляем критерий хи-квадрат Мак-Нимара
  

Е
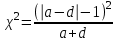
сли то Н(0) принимается

• 
  Если то принимаем Н(1),
  

Работа с преподавателем. Было проведено исследование эффективности антитабачной рекламы. Для этого сравнили соотношение курящих/некурящих до и после проведения рекламной компании.

Сформулируем Н(0): рекламная компания, проведенная в генеральной совокупности, не повлияет на долю курящих.

---

Или - соотношение курящих и некурящих среди членов генеральной совокупности после рекламной компании не изменится.

Зададим уровень значимости α=0,01

Рекламная компания была проведена среди 100 человек. В результате исследования были получены следующие результаты

	После рекламы
До рекламы	Не курят (-)	Курят (+)
Курят (+)	32 (курили , но не стали курить)	25 (курили и курят)
Не курят (-)	43 (не курили и не курят)	0 (не курили, но стали курить)

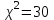
Мы задали 1% -ный уровень значимости α = 0,01 . Тогда критическое значение = 6,64 (по таблице для f=1). Полученное значение χ²=30 больше, чем критическое, следовательно:

мы отвергаем нулевую гипотезу и принимаем альтернативную о том, что с вероятностью 99 % рекламная компания повлияет на соотношение курящих и некурящих в популяции (генеральной совокупности).
Контрольные вопросы

1. 
   Для каких целей используются таблицы сопряженности
   
2. 
   Структура таблицы сопряженности
   
3. 
   Сформулирйте нулевую гипотезу для общего случая
   
4. 
   Какие данные заносятся в таблицу сопряженности в случае зависимых выборок
   
5. 
   Какие критерии используются при анализе таблицы сопряженности
   

Задание к теме.

1. 
   Сформулируйте цель проведенного исследования
   
2. 
   Сформулируйте нулевую и альтернативную гипотезы
   
3. 
   Составьте таблицу сопряженности
   
4. 
   Решите задачу на уровне значимости 0,05
   

---

Вариант 1

Исследовалась заболеваемость в сельской и городской местности. Выборочные исследования показали, что в селе из ста жителей обращались к врачу 36 человека, в городе из 100 жителей посетили врача 28 человек. Определить зависит ли обращаемость к врачу от места жительства.
Вариант 2.

Среди 84 лиц, страдающих гипертонией, с давлением более 160 мм.рт.ст. было 24 человека. После приема препарата их стало 18. Сделайте вывод об эффективности препарата.

Вариант 3

Сравнивалась эффективность двух методов лечения и получены следующие данные

	1 вид лечения	2 вид лечения
Вылечились	58	36
Не вылечились	54	19

Отличаются ли по эффективности эти два вида лечения?
Вариант 4

В конце первого года обучения в вузе в группе студентов из 15 человек было 6 отличников. В конце второго года обучения их стало 8. Определить, меняется ли успеваемость на втором курсе.

Вариант 5

1000 человек классифицировали по признаку дальтонизма. По приведенным ниже данным проверить, есть ли зависимость между наличием дальтонизма и полом человека.

	Мужчины	Женщины
Дальтоники	38	6
Не дальтоники	442	514

Вариант 6

Во время эпидемии гриппа изучалась эффективность прививок против этого заболевания. Получены следующие результаты:

С прививкой		Без прививки
заболели	не заболели	заболели	не заболели
4	192	34	111

---