Файл: Инструкция по регистрации на портале дистанционного образования moodle 3.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 365
Скачиваний: 1
СОДЕРЖАНИЕ
Инструкция по регистрации на портале дистанционного образования MOODLE
КРЕДИТ 1. ВЫБОРОЧНЫЙ МЕТОД В НАУЧНЫХ ИССЛЕДОВАНИЯХ
РАЗДЕЛ 1. ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Практическое занятие 1: Построение и описание гистограмм
Практическое занятие 2. Вычисление статистических характеристик случайных величин
Практическое занятие 3. Проверка гипотезы о нормальности распределения случайной величины.
Задание к теме: Проверка гипотезы о нормальности распределения случайной величины.
РАЗДЕЛ 2. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Практическое занятие 4. Критерий Стьюдента для анализа биомедицинских данных.
Практическое занятие 5. Непараметрические критерии проверки статистических гипотез.
Практическое занятие 6. Сравнение относительных величин
РАЗДЕЛ 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ
Практические занятие 7. Таблицы сопряженности
Практическое занятие 8. Линейная корреляция.
Практическое занятие 9. Прогнозирование на основе линейной регрессии
Практическое занятие 10. Метод однофакторного дисперсионного анализа.
Критические значения коэффициента асимметрии As
Критические значения коэффициента эксцесса Ех
Критические точки двустороннего t-критерия Стьюдента
Вариант 5.
| Объем циркулирующей крови (л) | 4,8 | 5,1 | 3,8 | 5,3 | 4,1 | 5,3 | Определите объем циркулирующей крови у лиц ростом 160 см. |
| Рост (см) | 170 | 175 | 150 | 175 | 155 | 180 |
Вариант 6.
| y | Латентный период (мс) | 15,7 | 13,6 | 25,6 | 34,6 | 48,5 | 41,6 | Определите латентный период при амплитуде потенциалов мозга 5 мкв. |
| x | Амплитуда потенциалов мозга (мкв) | 2,3 | 4,0 | 7,4 | 4,5 | 6,7 | 10,0 |
Вариант 7. Измерения длины головы (х) и длины грудного плавника (у) у окуней дали результаты (в мм).
| x | 66 | 61 | 67 | 73 | 51 | 59 | Определите длину грудного плавника у окуней при длине головы 80 мм. |
| у | 38 | 31 | 36 | 43 | 29 | 33 |
Вариант 8. Связь между массой тела (х) и количеством гемоглобина в крови (у) у павианов-гамадрилов характеризуется следующими данными.
| Масса тела, кг | 18 | 17,7 | 19 | 18 | 19 | 22 | Определите содержание гемоглобина при массе тела 25 кг. |
| Гемоглобин (по Сали) | 70 | 74 | 72 | 80 | 77 | 80 |
Вариант 9. Изменение урожайности по годам.
| Годы | 1926 | 1927 | 1928 | 1929 | 1930 | 1931 | Спрогнозируйте урожайность картофеля в 1932 году |
| Урожайность картофеля, (ц) | 7,2 | 7,1 | 7,4 | 6,1 | 6,0 | 7,3 |
Вариант 10.
По данным таблицы определить взаимосвязь между успеваемостью и временем, затрачиваемым на подготовку к занятиям.
| Успеваемость, % | 45 | 94 | 72 | 88 | 55 | Предположите какова будет успеваемость, если время на самоподготовку составит 18 час/нед |
| Время на самоподгтовку, час\нед. | 5 | 20 | 15 | 12 | 9 |
Вариант 11
| Физич. нагрузка, кг | 50 | 70 | 35 | 80 | 85 | 90 | Определите ЧСС при физическойнагрузке 65 кг. |
| ЧСС, уд/мин | 66 | 72 | 60 | 78 | 85 | 80 |
Вариант 12
| Показатель ожирения | 0,775 | 0,800 | 0,810 | 0,850 | 0,925 | 0,945 | Определите индекс чувствительности к инсулину при показателе ожирения 1,05 |
| Индекс чувствительности к инсулину | 1,322 | 1,301 | 1,130 | 1,021 | 1,106 | 1,041 |
Вариант 13
| х | Проницаемость сосудов сетчатки | 15 | 13,5 | 23,3 | 6,3 | 2,5 | 13 | Определите электрическую активность сетчатки при проницаемости сосудов = 20 |
| у | Электрическая активность сетчатки | 38,5 | 59 | 97,4 | 119,2 | 129,5 | 198,7 |
Вариант 14
| Возраст, лет | 55 | 63 | 49 | 58 | 38 | 36 | Определите АД в возрасте 40 лет |
| АД, мм.рт.ст. | 155 | 153 | 160 | 148 | 142 | 110 |
Вариант 15
| Возраст, лет | 64 | 45 | 68 | 42 | 76 | 34 | Определите АД в возрасте 55 лет |
| АД, мм.рт.ст. | 142 | 128 | 160 | 136 | 150 | 121 |
Задание к теме СРСП 8: Выполняется на платформе MOODLE
На платформе «MOODLE» найдите дисциплину «Биостатистика» и задание по СРСП 8 согласно своему варианту. После его выполнения введите ответы. Задание должно быть выполнено в течение срока изучения РАЗДЕЛА.
Практическое занятие 10. Метод однофакторного дисперсионного анализа.
Вопросы к теме
-
Понятие корреляции, линейная и нелинейная корреляция -
Коэффициент корреляции, пределы коэффициента корреляции, прямая и обратная корреляция -
Сильная, средняя и слабая корреляция, прямопропорциональная зависимость. -
Параметрический и непараметрический коэффициенты корреляции. Условия применения. -
Регрессия, линейная регрессия, уравнение линейной регрессии -
Нахождение коэффициентов уравнения линейной регрессии -
Практическое значение регрессионного анализа -
Понятие случайной величины -
Основные характеристики случайной величины -
Дисперсия, интерпретация дисперсии, формула вычисления дисперсии
Чтобы оценить влияние многоуровневого фактора на какой-то признак, необходимо вычислить отношение межгрупповой дисперсии к внутригрупповой дисперсии
-
Межгрупповая дисперсия вносится изучаемым фактором -
Внутригрупповая дисперсия вносится какими-то другими (неучтенными) факторами
Внутригрупповая дисперсия
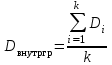
Где
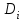 - дисперсия показателя в каждой из k групп
- дисперсия показателя в каждой из k группМежгрупповая дисперсия вычисляется по средним значениям в группах
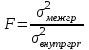
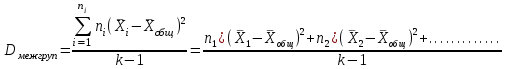
ni–количество объектов в i –той группе
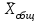 - общая средняя
- общая средняя-
Выдвигаем Н(0) – фактор не влияет на изучаемый признак -
Задаемся уровнем значимости α -
Вычисляем критерий Фишера
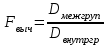
-
С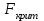 равниваем с для заданного α и числа степеней свободы (Приложение )
равниваем с для заданного α и числа степеней свободы (Приложение )
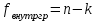
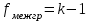
k – число групп, n-общее количество объектов обследования
-
Если вычисленное значение критерия Фишера меньше критического, то Н(0) принимается и делается вывод, что фактор не влияет на исследуемый показатель. -
В противном случае принимается Н(1)
Пример решения задачи
Задача. В табл. приведены данные по сравнению k = 4 разных рационов кормления на увеличение привеса животных у (в условных единицах). Эксперимент был полностью рандомизирован, каждый рацион испытывался на пiособях, выбранных в случайном порядке из группы 23 животных. Проверить нулевую гипотезу о том, что исследуемые рационы не отличаются по своему действию (вызываемому привесу животных).
| Рацион | овощи | мясо | макароны | обычн. | k= | |
| № живот. | Вес животных | | ||||
| 1 | 12 | 15 | 34 | 26 | | |
| 2 | 9 | 16 | 31 | 25 | | |
| 3 | 15 | 15 | 22 | 32 | | |
| 4 | 13 | 9 | 25 | 29 | | |
| 5 | 11 | 13 | 26 | 30 | | |
| 6 | | 12 | 27 | | | |
| 7 | | 18 | | | | |
| ni | | | | | n= | |
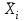 | | | | |  | |
 | | | | | Σ= | |