Файл: Инструкция по регистрации на портале дистанционного образования moodle 3.docx

Практическое занятие 2. Вычисление статистических характеристик случайных величин

Базовые вопросы к теме

1. 
   Цели биостатистики, предмет биостатистики
   
2. 
   Применение статистического анализа в медицинских исследованиях
   
3. 
   Понятие случайной величины
   
4. 
   Генеральная совокупность и выборка
   
5. 
   Классификация признаков: количественные и качественные признаки
   
6. 
   Правила построения гистограмм
   

Дидактический блок

С 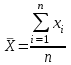реднее значение ( 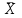)– характеристика положения значений случайной величины на оси измерений

Д 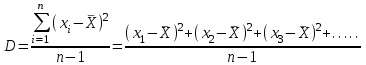исперсия (D) – характеристика разброса значений случайной величины относительно среднего значения


Стандартное отклонение (среднеквадратичное отклонение) –также является характеристикой разброса, введена для того, чтобы избавиться от квадрата единицы измерения



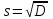
Коэффициент вариации  представляет собой относительную меру разброса, выраженную в процентах. Он вычисляется по формуле:



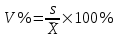
Коэффициент вариации:

• 
  используют для сравнения разброса двух и более признаков, имеющих различные единицы измерения.
  
• 
  он позволяет судить об однородности совокупности:
  

< 17% – абсолютно однородная;

17–33% – достаточно однородная;

35–40% – недостаточно однородная;

40–60% – это говорит о большом разбросе совокупности.

Т.е. считаем выборку однородной при V% ≤ 33%
Стандартная ошибка средней.


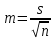
Мода (Мо) – наиболее часто встречающееся значение случайной величины. Для того, чтобы определить моду все значения выборки выстраиваются в ранжированный ряд (по возрастанию или по убыванию). Может быть несколько значений моды.

По ранжированному ряду находим и медиану (Ме

---

) – это значение случайной величины, которое делит выборку на две равные части. Если число объектов выборки четное, то медиана равна среднему двух соседних значений.

Нижний квартиль Q₂₅ – это значение случайной величины, ниже которого находится 25% выборки.

В ранжированном ряду нижний квартиль находится под номером, определяемым по формуле:



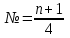
(округлить до ближайшего)

Верхний квартиль Q₇₅ – это значение случайной величины, выше которого находится 25% выборки.

В ранжированном ряду верхний квартиль находится под номером, определяемым по формуле :



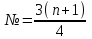
(округлить до ближайшего)

Межквартильный (интерквартильный) размах – это разница ΔQ=Q₇₅ - Q₂₅.

50 % данных лежит в пределах от нижнего до верхнего квартилей.

Если случайная величина имеет нормальное распределение, то

• 
  68,26% всех значений генеральной совокупности лежит в интервале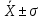
  
• 
  95,44% всех значений генеральной совокупности лежит в интервале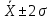
  
• 
  99,73% всех значений генеральной совокупности лежит в интервале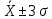
  

Пример расчета

Анализ роста мальчиков

n=11

х1

х2

х3

х4

х5

х6

х7

х8

х9

х10

х11

∑

Рост мальч.

186

178

167

170

168

172

182

176

170

188

170

1927

=175,18

Dх=54,56

sх=7,39

mх=2,23

V%=4,2%

Мо=170

Ме=172

Q25=170

Q75=182

Q75- Q25=12

---

Анализ роста девочек

n=11

y1

y2

y3

y4

y5

y6

y7

y8

y9

y10

y11

∑

Рост девоч.

161

168

164

163

165

160

165

165

169

170

168

1820

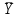=165,3

Dy=10,42

sy=3,23

my=0,97

V%=2%

Мо=165

Ме=165

Q25=163

Q75=168

Q75- Q25=5

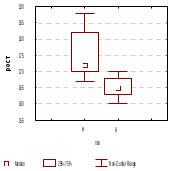
Анализ результатов:

1. 
   Мальчики более рослые, чем девочки – об этом свидетельствуют средние значения и положение выборок на числовой оси – выборка девочек расположена левее, т.е. в области меньших значений роста.
   

2. 
   Дисперсия роста мальчиков, больше дисперсии роста девочек. Т.е. разброс значений роста у мальчиков больше, т.е. среди них встречаются низкорослые, среднего роста и высокие. На это указывают также коэффициент вариации и межквартильный размах.
   

---

У девочек группа более однородная, т.е. они не сильно различаются по росту.

3. 
   У мальчиков наиболее часто встречается рост 170 см, об этом свидетельствует мода Мо. Половина мальчиков имеет рост меньше 172 см, на это указывает Ме. Т.е. в целом мальчики невысокие.
   
4. 
   У девочек наиболее часто встречается рост 165 см, об этом свидетельствует мода Мо. Половина девочек имеет рост меньше 165 см, на это указывает Ме. Т.е. в целом девочки также невысокие.
   

Контрольные вопросы:

1. 
   Понятие генеральной совокупности и выборки. Репрезентативность выборки
   
2. 
   Какую информацию о групповых свойствах отражает среднее значение. Приведите пример.
   
3. 
   Какую информацию о групповых свойствах отражает дисперсия, коэффициент вариации, стандартное отклонение. Приведите пример практического использования этих характеристик.
   
4. 
   Какую информацию о групповых свойствах отражает медиана. Приведите пример.
   
5. 
   В чем различия между медианой и средним значением, в каких случаях они совпадают и не совпадают.
   
6. 
   Как определить в каких пределах лежат все значения признака в генеральной совокупности
   
7. 
   Дайте интерпретацию стандартной ошибки среднего, как ее уменьшить
   
8. 
   Дайте определение квартилей. Какую информацию о групповых свойствах отражают нижний и верхний квартили.
   

Сравните две группы с указанием:

1. 
   Величины, вокруг которой группируются значения данного признака в каждой группе. Обоснуйте свой ответ.
   
2. 
   Являются ли первая и вторая группа однородными по данному признаку. Обоснуйте свой ответ.
   
3. 
   В какой группе разброс значений больше. Обоснуйте свой ответ.
   
4. 
   Какая величина встречается наиболее часто в каждой из групп
   
5. 
   На что указывает медиана признака в каждой из групп
   
6. 
   На что указывает межквартильный размах в каждой из групп.
   
7. 
   Предположив, что признак имеет нормальное распределение, определите в каких пределах лежат 95,44% всех значений признака в генеральной совокупности
   
8. 
   Представьте результаты вычислений в графическом виде
   

	Вариант 1		Вариант 2		Вариант 3		Вариант 4		Вариант 5		Вариант 6		Вариант 7
	Гемоглобиг, г/л		САД, мм.рт.ст		холестерин, ммоль/л		глюкоза, ммоль/л		ФЖЕЛ, литр		ОФВ, %		Индекс массы тела
	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.
	95	115	115	125	4,99	4,2	6,4	4	1,14	1,65	91	79	42,70	24,00
	95	120	120	128	4,01	5,6	6,7	4,7	2,72	2,14	59	79	35,30	28,00
	100	125	113	132	4,7	4	6,4	8,9	2,06	2,43	82	41	35,00	26,00
	115	125	110	120	5,19	3,9	10,1	4,1	2,84	3,5	96	53	36,10	30,00
	85	120	125	115	7,2	5	5,2	4,5	2,35	1,37	68	65	30,30	17,90
	88	115	130	135	4,32	4,5	4,7	4	2,99	2,22	101	42	36,03	27,60
	110	110	135	140	5,84	4,7	5,8	4,2	2,05	4,16	50	90	30,00	26,00
	103	130	120	145	20	4	10,9	4,6	1,63	2,15	94	121	30,10	29,00
	82	117	95	140	5,66	4,2	6,2	4	1,71	2,76	74	73	28,09	38,00
	75	118	110	135	4,88	5,1	6,3	4	2,53	2,23	79	99	27,90	35,00
	80	123	115	120	7,08	3,7	20,1	4,1	1,67	3,04	79	75	34,40	35,00
	93	125	120	128	5,76	3,5	5,2	4	2,29	2,05	85	120	19,00	35,00
	95	124	125	132	6,61	3,5	6,8	4	2,6	2,66	87	62	18,00	36,00
	98	116	130	136	4,9	5	4,7	4,9	1,58	1,3	39	65	23,40	22,00
	100	118	132	137	4,16	4,2	5,8	3,8	2,09	1,77	38	57	24,60	29,00
	103	135	140	142	4	4	10,4	3,1	1,97	2,39	84	77	36,00	36,00
	105	132	112	122	6,54	3,4	6,1	4,4	2,02	2,65	72	94	33,70	26,29
	120	128	113	120	5	4,1	5	4	2,02	3,48	71	111	20,40	32,00
	115	130	100	115	5,12	3,6	5,6	3,5	2,43	3,45	8	46	26,63	30,00
	125	130	95	118	3,9	4,2	5	3,6	2,01	2,33	58	80	40,00	23,00
	100	120	102	133	5,17	3,6	5,6	4,1	1,64	1,92	27	73	39,30	20,00
	95	125	103	142	20	3,1	5,2	3,5	2,47	3,32	127	55	26,71	26,00
	80	140	115	137	4,91	4	5,9	3,8	3,7	1,78	124	103	32,00	31,00
	85	135	116	128	6,49	4,3	4,9	4,1	2,58	1,57	80	66	26,30	32,00
	85	125	120	120	4,99	4	5,3	4,1	2,01	2,48	75	92	38,30	36,00

---

	Вариант 8		Вариант 9		Вариант 10		Вариант 11		Вариант 12		Вариант 13		Вариант 14
	Рост, см		Содержание Р в слюне, ммоль\л		Вес, кг		Объем циркулирующей плазмы, мл\кг		Пульс, уд\мин		Показатель гематокрита		Концентрация пролактина в крови (нг/мл)
	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.	1 гр.	2 гр.
	196	167	7	2,2	65	58	45	34	66	76	0,26	0,48	25	36
	175	177	3,7	4,5	70	70	36	32	72	72	0,12	0,1	120	120
	181	165	5,5	4,7	75	75	37	39	77	82	0,2	0,22	75	88
	181	195	3,1	2,3	68	88	38	42	80	80	0,28	0,16	50	50
	184	181	3,9	3,8	92	92	41	46	58	90	0,29	0,41	185	166
	154	194	4,5	5,7	88	81	42	41	75	75	0,21	0,23	125	125
	173	178	5,7	2,9	76	76	26	38	82	88	0,45	0,14	70	82
	169	177	4	5,9	73	66	31	28	78	78	0,38	0,33	145	145
	169	191	3,7	3,1	77	77	35	39	71	76	0,29	0,34	170	144
	163	175	6	6,7	102	90	40	27	62	62	0,24	0,35	80	80
	174	155	3,8	4,4	85	85	43	43	78	66	0,27	0,27	110	57
	192	175	5,4	4,7	69	100	36	33	76	76	0,18	0,24	87	87
	176	165	6,1	3,6	70	70	37	44	82	80	0,23	0,3	115	99
	177	170	3,9	6,9	77	52	36	34	82	82	0,3	0,17	130	130
	177	161	4,4	5,6	82	82	30	40	66	85	0,32	0,11	58	69
	180	178	5,6	3,5	66	77	26	31	60	78	0,18	0,15	122	122
	177	178	3,8	6,4	75	75	44	26	75	75	0,42	0,3	78	80
	155	176	2,4	3	69	88	30	33	78	75	0,36	0,28	110	110
	174	178	2,5	6,6	83	83	40	36	72	72	0,26	0,4	66	70
	167	185	3,6	4,7	74	70	31	37	68	80	0,29	0,23	92	92
	154	194	7	2,2	65	58	45	34	66	76	0,26	0,48	25	36
	173	178	3,7	4,5	70	70	36	32	72	72	0,12	0,1	120	120
	169	177	5,5	4,7	75	75	37	39	77	82	0,2	0,22	75	88
	169	191	3,1	2,3	68	88	38	42	80	80	0,28	0,16	50	50
	163	175	3,9	3,8	92	92	41	46	58	90	0,29	0,41	185	166

---