Файл: Инструкция по регистрации на портале дистанционного образования moodle 3.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 358
Скачиваний: 1
СОДЕРЖАНИЕ
Инструкция по регистрации на портале дистанционного образования MOODLE
КРЕДИТ 1. ВЫБОРОЧНЫЙ МЕТОД В НАУЧНЫХ ИССЛЕДОВАНИЯХ
РАЗДЕЛ 1. ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Практическое занятие 1: Построение и описание гистограмм
Практическое занятие 2. Вычисление статистических характеристик случайных величин
Практическое занятие 3. Проверка гипотезы о нормальности распределения случайной величины.
Задание к теме: Проверка гипотезы о нормальности распределения случайной величины.
РАЗДЕЛ 2. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Практическое занятие 4. Критерий Стьюдента для анализа биомедицинских данных.
Практическое занятие 5. Непараметрические критерии проверки статистических гипотез.
Практическое занятие 6. Сравнение относительных величин
РАЗДЕЛ 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ
Практические занятие 7. Таблицы сопряженности
Практическое занятие 8. Линейная корреляция.
Практическое занятие 9. Прогнозирование на основе линейной регрессии
Практическое занятие 10. Метод однофакторного дисперсионного анализа.
Критические значения коэффициента асимметрии As
Критические значения коэффициента эксцесса Ех
Критические точки двустороннего t-критерия Стьюдента
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ СТУДЕНТОВ
по БИОСТАТИТИКЕ
Оглавление
Инструкция по регистрации на портале дистанционного образования MOODLE 3
КРЕДИТ 1. ВЫБОРОЧНЫЙ МЕТОД В НАУЧНЫХ ИССЛЕДОВАНИЯХ 4
РАЗДЕЛ 1. ОПИСАТЕЛЬНАЯ СТАТИСТИКА 4
Практическое занятие 1: Построение и описание гистограмм 4
Практическое занятие 2. Вычисление статистических характеристик случайных величин 11
Практическое занятие 3. Проверка гипотезы о нормальности распределения случайной величины. 20
Задание к теме: Проверка гипотезы о нормальности распределения случайной величины. 23
РАЗДЕЛ 2. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ 26
Практическое занятие 4. Критерий Стьюдента для анализа биомедицинских данных. 26
Практическое занятие 5. Непараметрические критерии проверки статистических гипотез. 34
Практическое занятие 6. Сравнение относительных величин 40
РАЗДЕЛ 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ 45
Практические занятие 7. Таблицы сопряженности 45
Практическое занятие 8. Линейная корреляция. 51
Практическое занятие 9. Прогнозирование на основе линейной регрессии 55
Практическое занятие 10. Метод однофакторного дисперсионного анализа. 59
ПРИЛОЖЕНИЯ 64
Критические значения коэффициента асимметрии As 64
Критические значения коэффициента эксцесса Ех 64
Критические точки двустороннего t-критерия Стьюдента 65
Критические значения χ2 66
Критические значения U-критерия Манна-Уитни, α = 0,01. Двусторонний критерий 70
Критические значения парного Т-критерия Уилкоксона 71
Таблица критических значений коэффициента корреляции рангов Спирмена 72
Критические значения F-критерия Фишера 73
Формулы подсчета статистических показателей 76
Инструкция по регистрации на портале дистанционного образования MOODLE
-
Зайти на сайт по адресу http://moodle.kgmu.kz -
Кликнуть по вкладке «access my application» -
В правом верхнем углу выбрать язык и кликнуть «вход» -
Ввести пароль и логин, полученные вами в деканате, при этом логин состоит только из фамилии на латинице. Например: логин Smagulov, пароль @Kgmu2233 -
Далее кликнуть на Курс-Общая медицина- 1 курс-Основы научного мышления_Биостатистика -
Ввести кодовое слово, состоящее из номера вашей группы и фразы Biostat
Например: Biostat_1-001
-
На портале вы найдете все нужные вам материалы и задания
КРЕДИТ 1. ВЫБОРОЧНЫЙ МЕТОД В НАУЧНЫХ ИССЛЕДОВАНИЯХ
РАЗДЕЛ 1. ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Практическое занятие 1: Построение и описание гистограмм
Одним из способов представления и анализа случайных величин является построение гистограмм распределения. Гистограмма показывает, как часто встречаются те или иные значения случайной величины, по ней можно качественно оценить функцию плотности распределения.
Рассмотрим правило построения гистограмм на конкретном примере.
Работа с преподавателем.
Задача: Даны значения пульса у 25 испытуемых (объем выборки n=25). Представить выборку в виде таблицы частот и построить гистограмму.
70; 75; 63; 64; 72; 77; 80; 85; 79; 64; 63; 60; 55; 56; 58; 58; 73; 72; 65; 65; 66; 68; 69; 66; 68
Необходимо выполнить следующие шаги:
-
Элементы выборки объемом n=25 расположить в ранжированный ряд (по возрастанию или убыванию)
-
Вычислить размах R (разность между минимальным и максимальным значением случайной величины):
R=xmax-xmin=
-
Разбить вариационный ряд на k непересекающихся интервалов. k вычисляют по формуле Стерднесса, предусматривающей выделение оптимального числа интервалов:
k=1+3.322lg(n) (округлить до целого)
Можно воспользоваться следующими рекомендациями
| Объем выборки | Число интервалов |
| 25-40 | 5-6 |
| 41-60 | 6-8 |
| 61-100 | 7-10 |
| 101-200 | 8-12 |
| Более 200 | 10-15 |
-
Определить длину одного интервала:
b=R/k

-
Определить границы каждого интервала -
Определить частоты - количество ni элементов выборки, попавших в i-й интервал (элемент, совпадающий с правой границей интервала, относится к последующему интервалу)
Наряду с частотами одновременно подсчитываются также относительные частоты
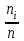
и процент случаев относительно общего объема выборки

Полученные результаты сводятся в таблицу, называемую таблицей частот группированной выборки.
Для нашей задачи результаты группировки представлены в следующей таблице:
| Номер интервала, i | Границы интервала | Частота, ni | Относительная частота  | Процент случаев |
| 1 | | | | |
| 2 | | | | |
| 3 | | | | |
| 4 | | | | |
| 5 | | | | |
| 6 | | | | |
| | ИТОГО | Σ= | Σ= | Σ= |
-
Далее строится гистограмма. По оси абсцисс откладываются интервалы, по оси ординат могут откладываться абсолютная частота встречаемости, или относительная частота встречаемости, или же процент относительно общего объема выборки.
В данном случае исследуемый признак – это пульс, который является случайной величиной X (x1, x2, x3 …..xi…… xn
)
Этот график дает нам информацию о законе распределения случайной величины и носит название гистограммы распределения. Он показывает, насколько часто встречаются те или иные значения случайной величины.
По оси ординат могут откладываться
-
Абсолютная частота встречаемости -
Процент относительно общего объема выборки

-
Относительная частота встречаемости
Огибающая гистограммы дает нам качественное представление о законе распределения случайной величины (иногда просто говорят распределение). Этот закон характеризует вероятность того, что случайная величина примет то или иное значение. Существует множество различных законов распределения. Наиболее распространенным является нормальное распределение – оно имеет симметричный колоколообразный вид.
Какую информацию дает нам этот график.
Самостоятельная работа: Согласно своему варианту для случайной величины из таблицы данных построить гистограмму распределения. Описать полученные результаты.
| ВАРИАНТ | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Рост, см | Рост, см | Содержание Р в слюне, ммоль\л | Содержание Р в слюне, ммоль\л | Вес, кг | Вес, кг | Объем циркулирующей плазмы, мл\кг | Объем циркулирующей плазмы, мл\кг | Пульс, уд\мин | Пульс, уд\мин | Показатель гематокрита | Показатель гематокрита | Концентрация пролактина в крови (нг/мл) | Содержание андростеронов в моче (мг/сутки) | Концентрация пролактина в крови (нг/мл) |
| 196 | 167 | 7 | 2,2 | 65 | 58 | 45 | 34 | 66 | 76 | 0,26 | 0,48 | 25 | 0,82 | 36 |
| 175 | 177 | 3,7 | 4,5 | 70 | 70 | 36 | 32 | 72 | 72 | 0,12 | 0,1 | 120 | 0,9 | 120 |
| 181 | 165 | 5,5 | 4,7 | 75 | 75 | 37 | 39 | 77 | 82 | 0,2 | 0,22 | 75 | 0,98 | 88 |
| 181 | 195 | 3,1 | 2,3 | 68 | 88 | 38 | 42 | 80 | 80 | 0,28 | 0,16 | 50 | 1,06 | 50 |
| 184 | 181 | 3,9 | 3,8 | 92 | 92 | 41 | 46 | 58 | 90 | 0,29 | 0,41 | 185 | 1,2 | 166 |
| 154 | 194 | 4,5 | 5,7 | 88 | 81 | 42 | 41 | 75 | 75 | 0,21 | 0,23 | 125 | 1,29 | 125 |
| 173 | 178 | 5,7 | 2,9 | 76 | 76 | 26 | 38 | 82 | 88 | 0,45 | 0,14 | 70 | 1,48 | 82 |
| 169 | 177 | 4 | 5,9 | 73 | 66 | 31 | 28 | 78 | 78 | 0,38 | 0,33 | 145 | 1,42 | 145 |
| 169 | 191 | 3,7 | 3,1 | 77 | 77 | 35 | 39 | 71 | 76 | 0,29 | 0,34 | 170 | 1,4 | 144 |
| 163 | 175 | 6 | 6,7 | 102 | 90 | 40 | 27 | 62 | 62 | 0,24 | 0,35 | 80 | 1,08 | 80 |
| 174 | 155 | 3,8 | 4,4 | 85 | 85 | 43 | 43 | 78 | 66 | 0,27 | 0,27 | 110 | 1,11 | 57 |
| 192 | 175 | 5,4 | 4,7 | 69 | 100 | 36 | 33 | 76 | 76 | 0,18 | 0,24 | 87 | 1,32 | 87 |
| 176 | 165 | 6,1 | 3,6 | 70 | 70 | 37 | 44 | 82 | 80 | 0,23 | 0,3 | 115 | 1,12 | 99 |
| 177 | 170 | 3,9 | 6,9 | 77 | 52 | 36 | 34 | 82 | 82 | 0,3 | 0,17 | 130 | 1,26 | 130 |
| 177 | 161 | 4,4 | 5,6 | 82 | 82 | 30 | 40 | 66 | 85 | 0,32 | 0,11 | 58 | 0,88 | 69 |
| 180 | 178 | 5,6 | 3,5 | 66 | 77 | 26 | 31 | 60 | 78 | 0,18 | 0,15 | 122 | 1,16 | 122 |
| 177 | 178 | 3,8 | 6,4 | 75 | 75 | 44 | 26 | 75 | 75 | 0,42 | 0,3 | 78 | 1,3 | 80 |
| 155 | 176 | 2,4 | 3 | 69 | 88 | 30 | 33 | 78 | 75 | 0,36 | 0,28 | 110 | 1,2 | 110 |
| 174 | 178 | 2,5 | 6,6 | 83 | 83 | 40 | 36 | 72 | 72 | 0,26 | 0,4 | 66 | 0,84 | 70 |
| 167 | 185 | 3,6 | 4,7 | 74 | 70 | 31 | 37 | 68 | 80 | 0,29 | 0,23 | 92 | 0,96 | 92 |
| 180 | 178 | 5,6 | 3,5 | 66 | 77 | 26 | 31 | 60 | 78 | 0,18 | 0,15 | 122 | 1,16 | 122 |
| 177 | 178 | 3,8 | 6,4 | 75 | 75 | 44 | 26 | 75 | 75 | 0,42 | 0,3 | 78 | 1,3 | 80 |
| 155 | 176 | 2,4 | 3 | 69 | 88 | 30 | 33 | 78 | 75 | 0,36 | 0,28 | 110 | 1,2 | 110 |
| 174 | 178 | 2,5 | 6,6 | 83 | 83 | 40 | 36 | 72 | 72 | 0,26 | 0,4 | 66 | 0,84 | 70 |
| 167 | 185 | 3,6 | 4,7 | 74 | 70 | 31 | 37 | 68 | 80 | 0,29 | 0,23 | 92 | 0,96 | 92 |
Задание к ТЕМЕ 1 Опишите приведенную ниже гистограмму с указанием:
-
общего количества обследованных. -
минимального и максимального значения анализируемой величины, (с указанием в скольких процентов случаев) -
наиболее часто и редко встречающегося значения анализируемой величины (с указанием в скольких процентов случаев) -
в каких пределах в основном лежит анализируемая величина. -
дайте качественную оценку функции плотности распределения данной случайной величины (нормальное или отличное от нормального).
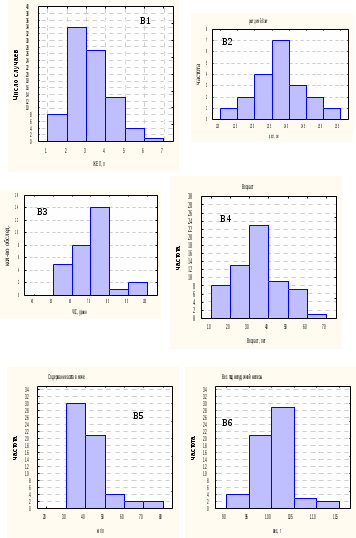
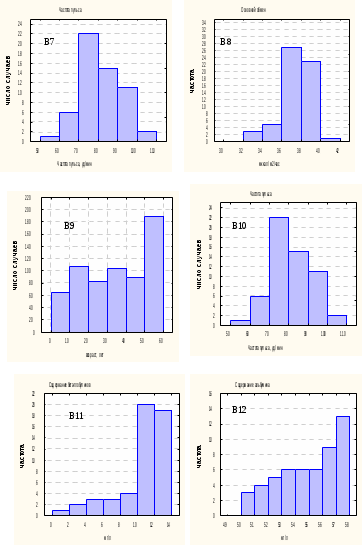
Контрольные вопросы
-
Основные задачи биостатистики -
Какую информацию несет гистограмма -
Что понимается под термином «распределение» -
Какая величина откладывается по оси ординат при построении гистограммы -
Какая величина откладывается по оси абсцисс при построении гистограммы -
Как определяется число интервалов при построении гистограммы -
Какими свойствами обладает нормальное распределение -
В каком случае две совокупности считаются не отличающимися по данному признаку -
При каких условиях две нормально распределенные совокупности не отличаются по данному признаку.
Задание к теме СРСП 1: Выполняется на платформе MOODLE
На платформе «MOODLE» найдите дисциплину «Биостатистика» и задание по СРСП 1 согласно своему варианту. После его выполнения введите ответы. Задание должно быть выполнено в течение срока изучения РАЗДЕЛА.