Файл: Методические указания по выполнению расчётнографической работы и организации самостоятельной работы содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 323
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮРАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №2
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №3
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №5
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕЗАДАНИЯ №5
ПО ТЕМЕ «ТРЕНД-СЕЗОННЫЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №6
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕ
ЗАДАНИЯ №5
1. Чем регрессионная модель отличается от функции регрессии?
2. В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?
3. В чем суть метода наименьших квадратов?
4. Приведите формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.
5. Объясните суть коэффициента детерминации. В каких пределах изменяется коэффициент детерминации.
6. Действительно ли для парной линейной регрессии коэффициент корреляции превосходит коэффициент детерминации?
7. Объясните экономический смысл коэффициента регрессии.
8. Какой смысл может иметь свободный коэффициент уравнения регрессии?
9. Объясните статистический смысл коэффициента детерминации.
10. Как записываются основная и альтернативная гипотезы при проверке адекватности уравнения регрессии в целом?
11. Как F-статистика связана с коэффициентом детерминации в парной регрессии?
12. Как рассчитать критерий Стьюдента для коэффициента регрессии в линейной модели парной регрессии?
13. В чем смысл средней ошибки аппроксимации?
14. Приведите схему определения интервальных оценок коэффициентов регрессии.
15. В каком месте доверительный интервал прогноза по парной модели является наименьшим?
ЗАДАНИЕ №6
ПО ТЕМЕ «ТРЕНД-СЕЗОННЫЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ»
ИСХОДНЫЕ ДАННЫЕ:
Индивидуальные исходные данные по вариантам для задания №6 приведены в файле MS Excel «Исходные данные задания №6 РГР».
ЗАДАНИЕ:
Данное задание РГР состоит из двух частей: Задания 1 и Задания 2.
Задание 1
Имеются поквартальные данные о доходах предприятия за 4 года, млн. руб. Построить аддитивную модель временного ряда и получить прогноз доходов на два следующих квартала.
Для этого необходимо:
-
Сформировать расчетную таблицу: Скользящая средняя за 4 квартала, Центрированная скользящая средняя, Оценка сезонной вариации, S,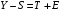 , T, T+S,
, T, T+S, 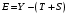 .
. -
Выполнить расчет скользящей средней за 4 квартала: просуммировать уровни ряда за каждые четыре квартала со сдвигом на один момент времени. Разделив полученные суммы на 4, найдем скользящие средние. -
Выполнить расчет центрированной скользящей средней: найти центрированные скользящие средние как средние значения из двух последовательных скользящих средних. -
Выполнить оценку сезонной вариации S: найти разность между уровнями и центрированными скользящими средними. -
Выполнить расчет скорректированной сезонной компоненты в таблице:
Год
№ квартала
1
2
3
4
1
2
3
4
Итого
Среднее
S
-
Выполнить расчет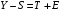 .
. -
Используя статистическую функцию Тенденция к столбцу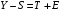 , выполнить расчет T для t=1…16.
, выполнить расчет T для t=1…16. -
Выполнить расчет T+S,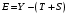 для t=1…16.
для t=1…16. -
Продлить переменную t значениями 17, 18. Получить прогноз тренда Т, продлив функцию Тенденция на значение t=17, затем на значение t=18. -
Получить прогноз дохода, просуммировав T17 и T18 со значениями S1 и S2 соответственно.
Задание 2
Имеются поквартальные данные о прибыли предприятия за 4 года, млн. руб. Построить мультипликативную модель временного ряда и получить прогноз прибыли на два следующих квартала.
Для этого необходимо:
-
Сформировать расчетную таблицу: Скользящая средняя за 4 квартала, Центрированная скользящая средняя, Оценка сезонной вариации, S,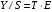 , T,
, T, 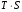 ,
, 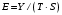 .
. -
Выполнить расчет скользящей средней за 4 квартала: просуммировать уровни ряда за каждые четыре квартала со сдвигом на один момент времени; разделить полученные суммы на 4, найдем скользящие средние. -
Выполнить расчет центрированной скользящей средней: найти центрированные скользящие средние как средние значения из двух последовательных скользящих средних. -
Выполнить оценку сезонной вариации S: найти отношение между уровнями и центрированными скользящими средними. -
Выполнить расчет скорректированной сезонной компоненты в таблице:
Год
№ квартала
1
2
3
4
1
2
3
4
Итого
Среднее
S
-
Выполнить расчет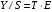 .
. -
Используя статистическую функцию Тенденция к столбцу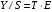 , выполнить расчет T для t=1…16.
, выполнить расчет T для t=1…16. -
Выполнить расчет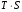 ,
, 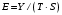 для t=1…16.
для t=1…16. -
Продлить переменную t значениями 17, 18. Получить прогноз тренда Т, продлив функцию Тенденция на значение t=17, затем на значение t=18. -
Получить прогноз прибыли, умножив T17 и T18 со значениями S1 и S2 соответственно.
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ
ЗАДАНИЯ №6
Комментарий: Существует принципиальное различие между анализом перекрестных выборок (cross-section) и временных рядов (time series): наблюдения во временных рядах строго упорядочены, тогда как порядок наблюдений в перекрестных выборках можно менять произвольно. Переставлять и удалять отдельные наблюдения во временных рядах нельзя, так как из-за этого меняется закономерность развития временного ряда.
Случайный процесс – процесс, реализациями которого в каждый момент времени являются случайные величины. В анализе временных рядов различают слабо стационарные и сильно стационарные случайные процессы. Также в анализе временных рядов предполагается, что значения исследуемой случайной величины являются непрерывными, а время является дискретным. Сильно стационарным процессом является процесс, для которого совместная функция распределения n последовательных элементов не меняется во времени. Процесс является слабо стационарным, если его математическое ожидание, дисперсия и автоковариационная функция не зависят от времени (при этом, конечно, предполагается, что все необходимые величины существуют и конечны). В практических приложениях требование сильной стационарности излишне, а слабая стационарность (синоним – стационарность) может обеспечить хорошие свойства процесса. Для характеристики процесса выполняется проверка временного ряда на стационарность (тест Дики – Фуллера, тест Квятковски – Филлипса – Шмидта – Шина). Наиболее распространенными линейными моделями стационарных временных рядов, используемыми для прогноза, являются модели AR(p) – авторегрессии, MA(q) – скользящего среднего, ARMA (p,q) –авторегрессии и скользящего среднего.
Большинство процессов экономике являются нестационарными. Нестационарность ведет к тому, что при росте размера выборки математическое ожидание, дисперсия и автоковариационная функция изменяются во времени. Различают нестационарные процессы с детерминистическим трендом и со стохастическим трендом. Наиболее распространенной моделью прогноза временного ряда нестационарного процесса со стохастическим трендом является модель ARIMA (p,d,q). Для моделирования детерминистического тренда используются линейные и нелинейные модели регрессии, а также тренд-сезонные модели (аддитивные или мультипликативные), когда наряду с трендом во временном ряде присутствует сезонная компонента.
Анализ временного ряда начинается с его графической визуализации и тестирования на стационарность. Затем выполняется выбор модели, приемлемой для прогноза.
Задание 1. Имеются поквартальные данные о доходах предприятия за 4 года, млн. руб. Построить аддитивную модель временного ряда и получить прогноз доходов на два следующих квартала.
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
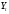 | 6 | 4,4 | 5 | 9 | 7,2 | 4,8 | 6 | 10 |
| t | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
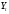 | 8 | 5,6 | 6,4 | 11 | 9 | 6,6 | 7 | 10,8 |
Для этого необходимо:
-
Сформировать расчетную таблицу: Скользящая средняя за 4 квартала, Центрированная скользящая средняя, Оценка сезонной вариации, S, , T, T+S,
, T, T+S,  .
. -
Выполнить расчет скользящей средней за 4 квартала: просуммировать уровни ряда за каждые четыре квартала со сдвигом на один момент времени. Разделив полученные суммы на 4, найдем скользящие средние. -
Выполнить расчет центрированной скользящей средней: найти центрированные скользящие средние как средние значения из двух последовательных скользящих средних. -
Выполнить оценку сезонной вариации S: найти разность между уровнями и центрированными скользящими средними. -
Выполнить расчет скорректированной сезонной компоненты в таблице:
Год
№ квартала
1
2
3
4
1
2
3
4
Итого
Среднее
S
-
Выполнить расчет .
. -
Используя статистическую функцию Тенденция к столбцу , выполнить расчет T для t=1…16.
, выполнить расчет T для t=1…16. -
Выполнить расчет T+S, для t=1…16.
для t=1…16. -
Продлить переменную t значениями 17, 18. Получить прогноз тренда Т, продлив функцию Тенденция на значение t=17, затем на значение t=18. -
Получить прогноз дохода, просуммировав T17 и T18 со значениями S1 и S2 соответственно.