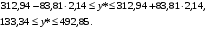Файл: Методические указания по выполнению расчётнографической работы и организации самостоятельной работы содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 322
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮРАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №2
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №3
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №5
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕЗАДАНИЯ №5
ПО ТЕМЕ «ТРЕНД-СЕЗОННЫЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №6
-
Чтобы рассчитать значение статистики Фишера, необходимо использовать ссылки на необходимые ячейки согласно формуле: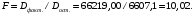
-
Чтобы проверить результат вычисления статистики с использованием коэффициента детерминации и статистики Стьюдента для β, необходимо использовать ссылки на необходимые ячейки согласно формулам: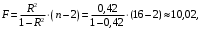
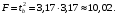
-
Для нахождения критического значения статистики Фишера удобно использовать функцию FРАСПОБР(…). В Главном меню MS Excel выберем: Формулы – Вставить функцию – Полный алфавитный перечень –
FРАСПОБР(…) (рис. 10).
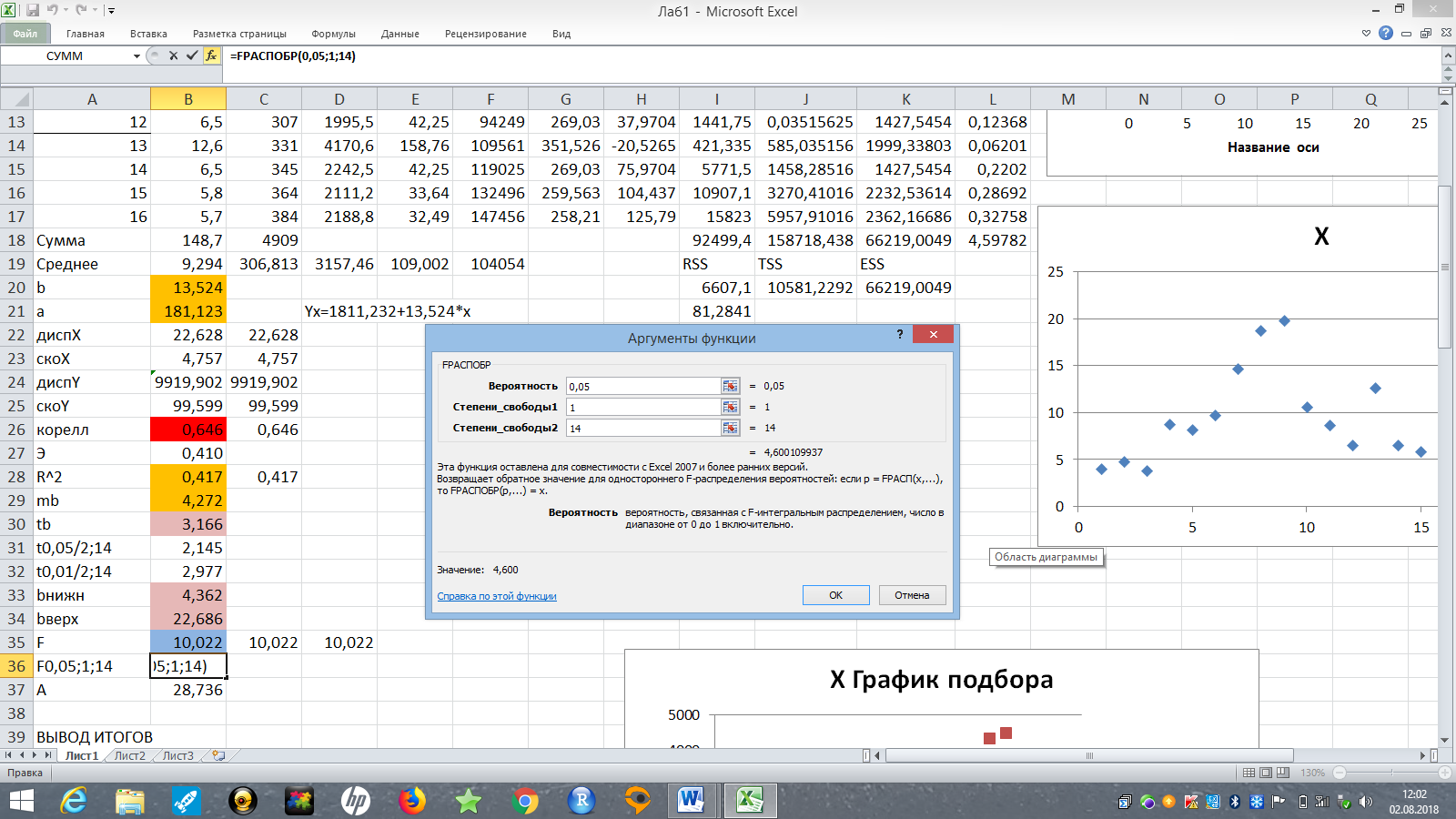
Рис. 10. Диалоговое окно функции FРАСПОБР(…).
Вывод 8: Поскольку 10,02 > 4,60, то гипотеза Н0: β = 0 отвергается, т.е. согласно тесту Фишера регрессия адекватна. Это означает, что между переменными x (расходы на рекламу) и y (объем продаж) существует значимая линейная связь.
Комментарий: В модели парной линейной регрессии не возникает вопрос о совокупном влиянии нескольких переменных, который актуален для множественной регрессии. Для того, чтобы определить, есть ли линейная зависимость между переменными x (расходы на рекламу) и y (объем продаж), достаточно проверить значимость коэффициента β при переменной x по тесту Стьюдента. Поэтому для проверки адекватности парной регрессии достаточно выполнить только тест Стьюдента.
-
Чтобы проверить качество регрессии по средней относительной ошибке аппроксимации, необходимо в таблице 1 заполнить столбец и использовать ссылки на необходимые ячейки согласно формуле:
и использовать ссылки на необходимые ячейки согласно формуле: 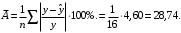
Вывод 9: Допустимый интервал средней ошибки аппроксимации – от 4% до 7%. Для построенной линейной парной регрессии средняя ошибка аппроксимации составила 28,74%, значит, качество подгонки модели рекомендуется улучшать, возможно, путем расширения модели до множественной регрессии через включение в нее дополнительных регрессоров.
-
Нажав на кнопку Анализ данных, следует выбрать опцию Регрессия (рис. 11).
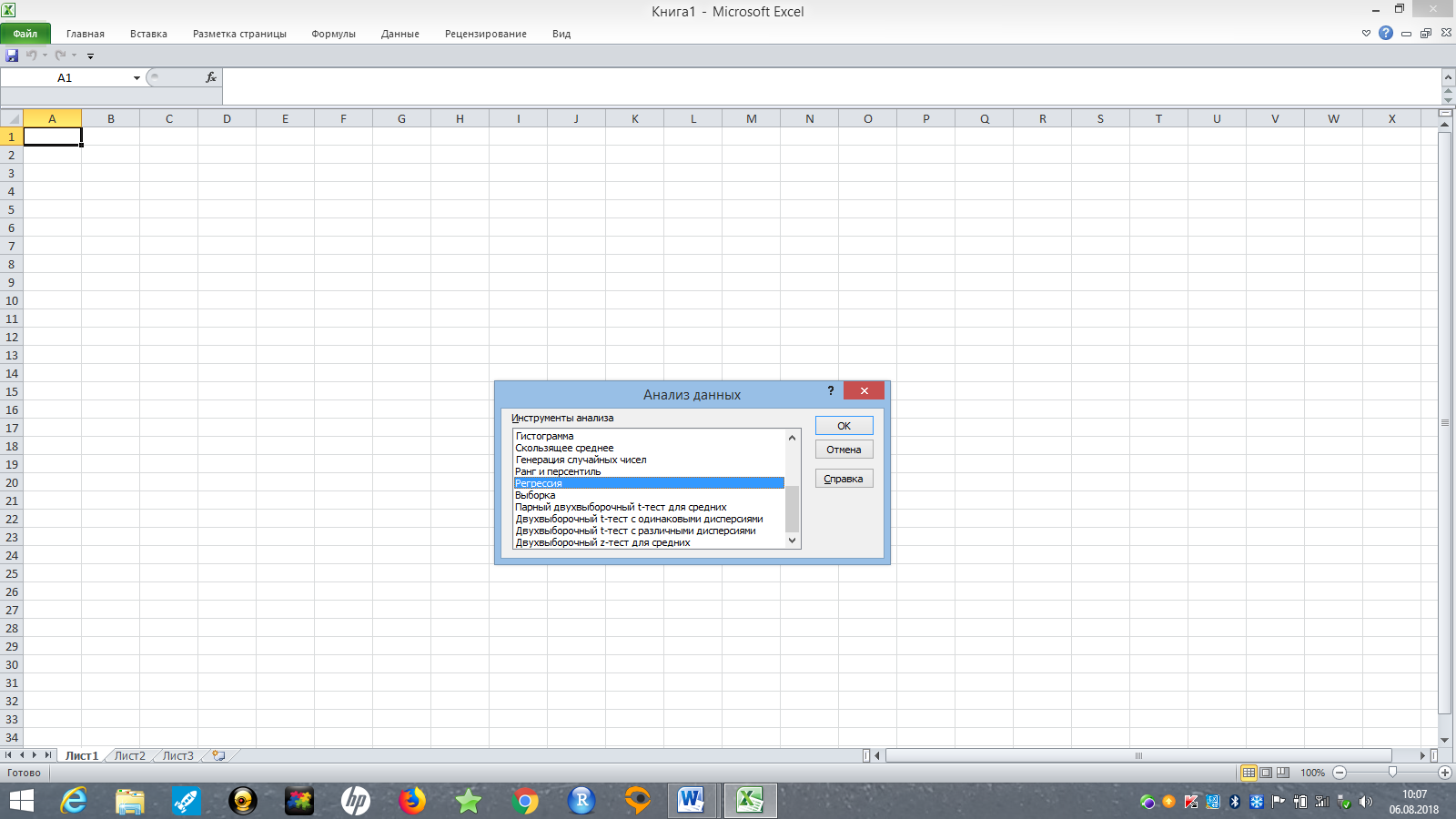
Рис. 11. Выбор регрессионного анализа в MS Excel
На экране появится новое окно с опциями регрессионного анализа (рис. 12).
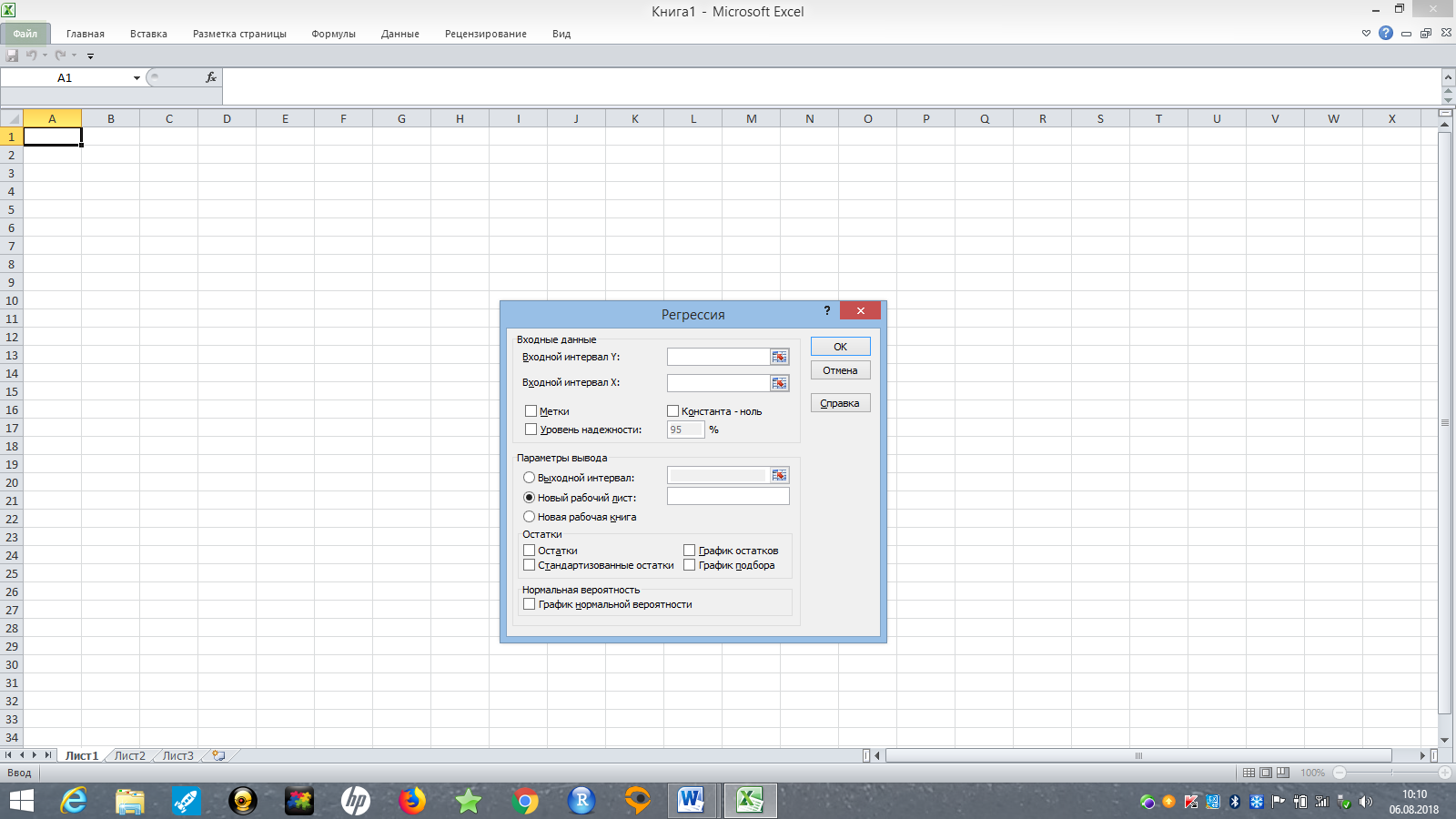
Рис. 12. Окно параметров регрессии в MS Excel
В поле Входной интервал y необходимо выбрать столбик, который будет отвечать за значения регрессанта – зависимой переменной (это может быть лишь один столбик).
В графе Входной интервал xнеобходимо выбрать столбики, которые содержат значения регрессоров.
Опция Метки, если в ней указать «галочку», трактует первую строку данных как названия переменных. Опция Константа – ноль позволяет строить модели без константы.
Опция Уровень надежности позволяет установить значение 1-α для данной модели (где α – уровень значимости).
В разделе Параметры вывода можно устанавливать, куда выводятся результаты регрессии (обычно выводят результаты на этот же лист, так как удобно держать данные и результаты оценки модели на одном листе).
С помощью опции Остатки модели можно получить ряд остатков модели. С помощью опции Стандартизированные остатки вы можете получить ряд остатков, деленных на свое стандартное отклонение. График остатков отражает зависимость значения остатков от значений каждого регрессора. График подбора показывает зависимость фактических значений регрессанта от каждого регрессора и зависимость предсказанных значений регрессанта от каждого регрессора. Таким образом, благодаря этому графику можно судить о качестве подгонки модели.
При построении графика нормальной вероятности по оси ординат откладываются значения регрессанта, а по оси абсцисс – процентили нормального распределения.
Чтобы оценить нашу регрессию в Excel в качестве регрессанта выберем переменную y – объем продаж, а в качестве регрессора выберем переменную x – расходы на рекламу, укажем «галочку» в опции Метки, чтобы трактовать первую строку данных как названия переменных (рис. 13).
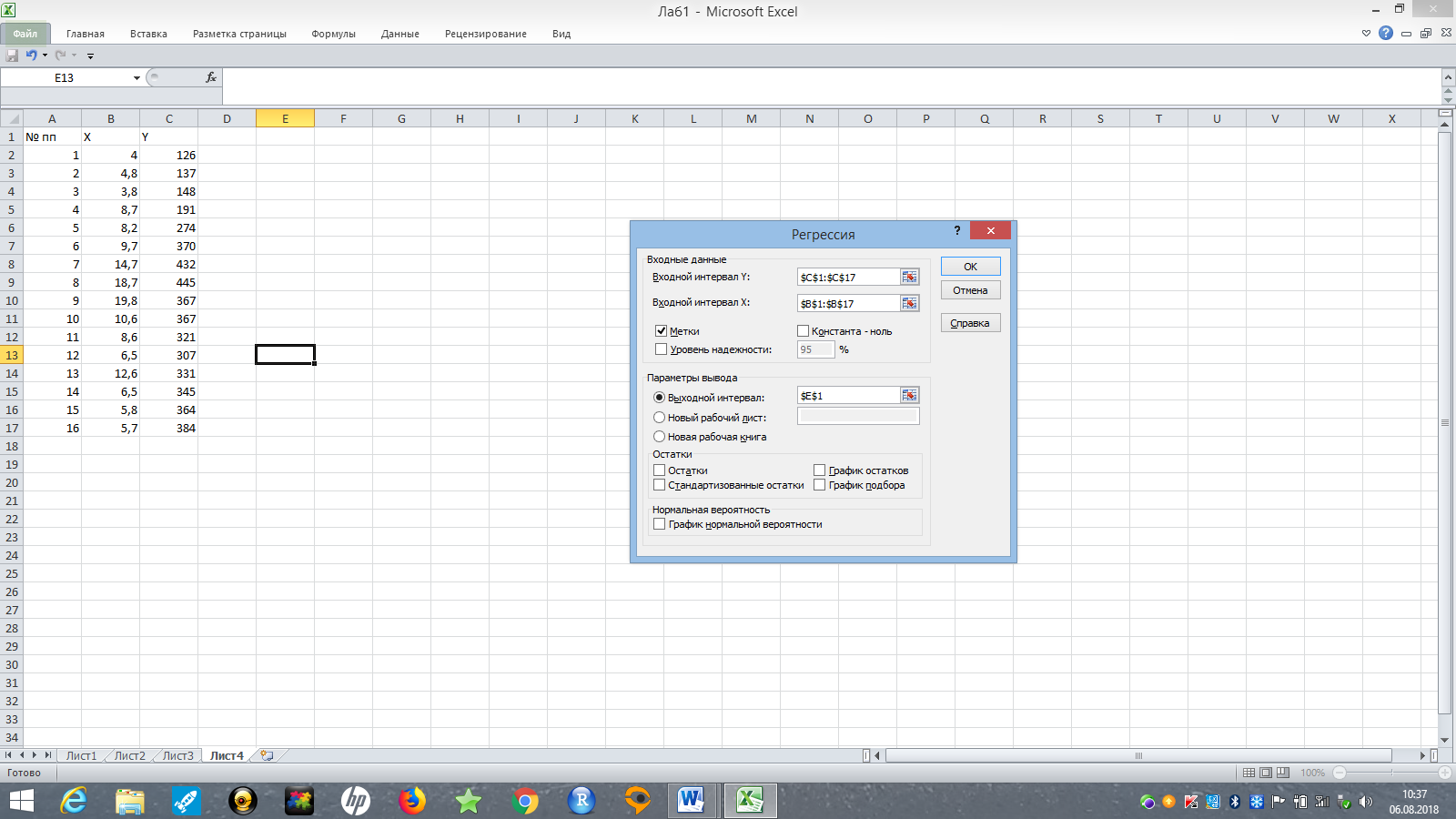
Рис. 13. Окно параметров регрессии с введенными значениями в MS Excel
Далее, нажав на кнопку Ок, получаем результаты (рис. 14).
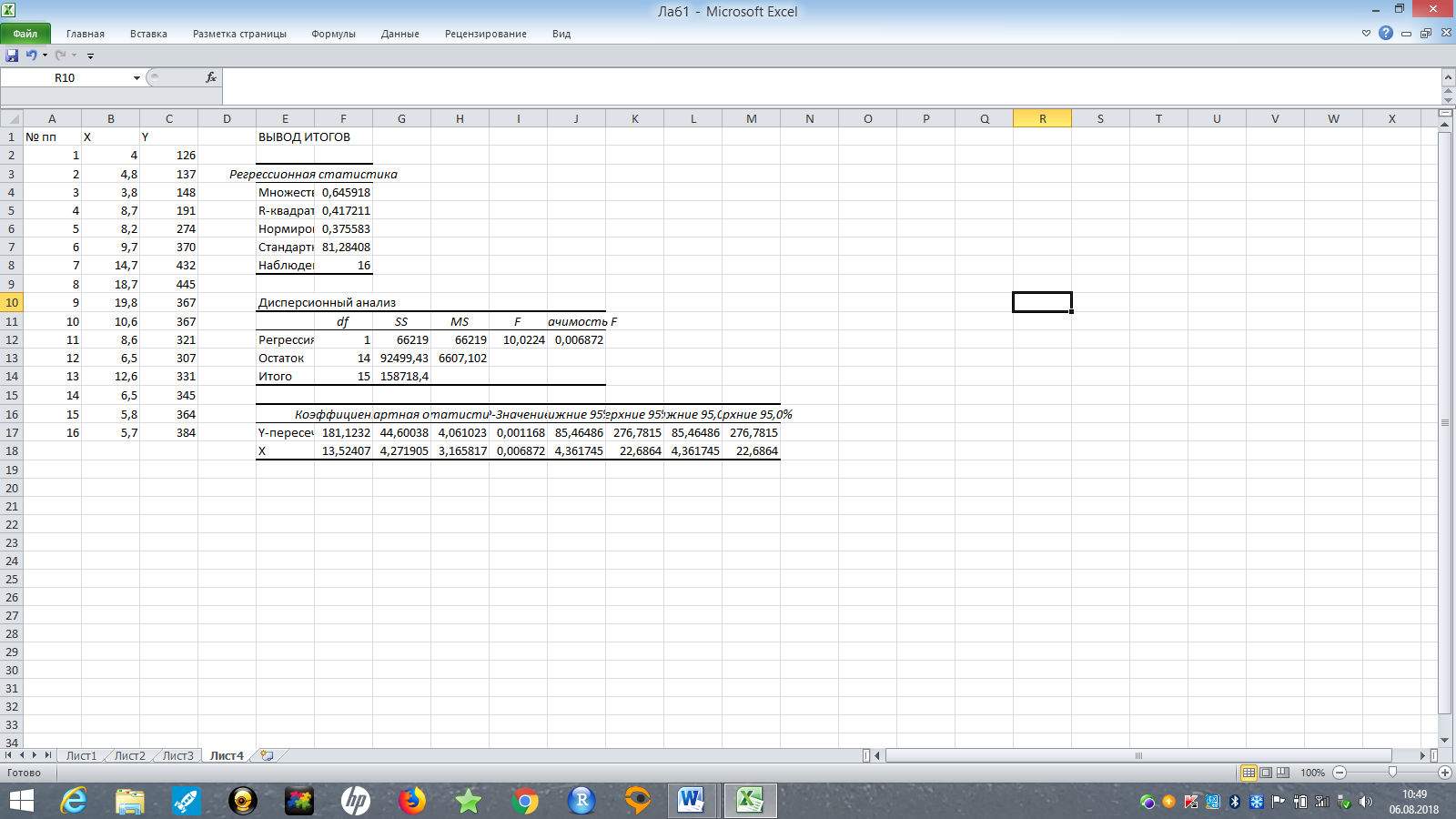
Рис.14. Вывод результатов оценивания регрессии в MS Excel
Более подробно рассмотрим результаты, переведя их в обычные таблицы.
| Регрессионная статистика | ||||||||
| Множественный R | 0,64592 | |||||||
| R-квадрат | 0,417211 | |||||||
| Нормированный R-квадрат | 0,375583 | |||||||
| Стандартная ошибка | 81,28408 | |||||||
| Наблюдения | 16 | |||||||
| Дисперсионный анализ | ||||||||
| | df | SS | MS | F | Значимость F | |||
| Регрессия | 1 | 66219 | 66219 | 10,0224 | 0,006872 | |||
| Остаток | 14 | 92499,43 | 6607,102 | | | |||
| Итого | 15 | 158718,4 | | | | |||
| | | | | | | |||
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | ||
| Y-пересечение | 181,1232 | 44,60038 | 4,061023 | 0,001168 | 85,46486 | 276,7815 | ||
| x | 13,52407 | 4,271905 | 3,165817 | 0,006872 | 4,361745 | 22,6864 | ||
В подтаблице «Регрессионная статистика» Множественный R – это коэффициент корреляции между регрессантом и регрессором. Строкой ниже Excel выдает значение R2, равное 0,42. Чуть ниже можно увидеть значение нормированного (или, по-другому, скорректированного (adjusted) R2. Еще ниже указано значение Стандартной ошибки регрессии (MSE) – квадратного корня из остаточной дисперсии (пересечение столбца MS и строки Остаток по второй подтаблице), равное 81,28. В конце подтаблицы дано значение количества Наблюдений, равное 16.
В подтаблице «Дисперсионный анализ» во втором столбце df даны числа степеней свободы, в третьем столбце даны значения ESS, RSS и TSS (соответственно 66219; 92499,43; 158718,4). Четвертый столбик содержит отношения ESS/dfESS, RSS/dfRSS соответственно. F – это значение F-статистики теста Фишера для проверки значимости регрессии. В самом правом столбце дано значение p-value для этой статистики. Значение p-valueпозволяет провести тест (в данном случае тест Фишера), не пользуясь критическими значениями статистики. Если p-value для статистики меньше, чем α =0,1, то нулевая гипотеза отвергается с вероятностью 90%. Если p-value для статистики меньше, чем α =0,05, то нулевая гипотеза отвергается с вероятностью 95%. Если p-value для статистики меньше, чем α =0,01, то нулевая гипотеза отвергается с вероятностью 99%. В нашем случае p-value для статистики Фишера составило 0,007, что меньше, чемα =0,01. Это означает, что с вероятностью 99% отвергается нулевая гипотеза о незначимости уравнения регрессии. Согласно тесту Фишера регрессия адекватна, между переменными x и Y существует значимая линейная связь.
В нижней подтаблице в столбце «Коэффициенты» содержатся коэффициент регрессии, равный 13,52, а также свободный коэффициент, равный 181,12 на пересечении со строкой «Y-пересечение». В третьем столбце указаны стандартные ошибки коэффициентов, далее – значение t-статистики теста Стьюдента, затем дано значение p-value для этой статистики. В нашем случае p-value для статистики Стьюдента для коэффициента регрессии составило 0,007, что меньше, чемα =0,01. Это означает, что коэффициент регрессии β является значимым, между переменными x (расходы на рекламу) и y (объем продаж) существует значимая линейная связь. Также p-value для статистики Стьюдента для свободного коэффициента составило 0,001, что меньше, чем α =0,01. Это означает, что свободный коэффициент α является значимым. В двух самых правых столбцах даны доверительные границы коэффициентов. В нашем случае, границы значение «ноль» не включают, что еще раз подтверждает статистическую значимость (отличие от нуля) коэффициентов уравнения регрессии.
Чтобы спрогнозировать расходы на рекламу в 1 квартале следующего года, надо среднее значение x увеличить на 5 %: 9,29*1,05 = 9,75 тыс. руб.
-
Получим прогноз объема продаж в 1 квартале следующего года: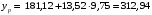 тыс. руб.
тыс. руб. -
Чтобы построить 95% -й интервал прогноза объема продаж в 1 квартале следующего года, необходимо использовать ссылки на необходимые ячейки согласно формуле:
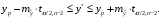
В данной формуле
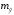 – стандартная ошибка прогноза. Ее можно определить для среднего прогнозного значения и для индивидуального прогнозного значения:
– стандартная ошибка прогноза. Ее можно определить для среднего прогнозного значения и для индивидуального прогнозного значения:a) для среднего прогнозного значения:
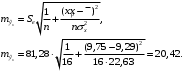
Тогда доверительный интервал прогноза среднего объема продаж с вероятностью 95% составит:
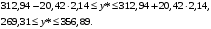
б) для индивидуального прогнозного значения:
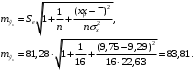
Тогда доверительный интервал прогноза индивидуального объема продаж с вероятностью 95% составит: