Файл: Informatika2013-Of2010.doc

– на рабочем листе, в ячейке, например, А1 записать значение левой границы для первого ограничения (число 3);

– в ячейке В1 записать значение левой границы для второго ограничения (число 0);

– в ячейке С1 записать целевую функцию:

=1,7 + 4,56 ∙ А1 – 3 ∙ В1 – 0,69 ∙ А1 ∙ В1 –0,44 ∙ В1^2

– выполнить Данные / Анализ / Поиск решения (если данной команды нет, то её нужно добавить, для чего выполнить Файл / Надстройки, в появившемся окне выбрать Поиск решения и нажать кнопку Перейти.)

В появившемся окне задать имя ячейки с целевой функцией (для данного примера С1), определить, что в задаче целевая функция стремится к максимуму, ввести соответствующие ограничения для содержимого ячеек А1 и В1.

Решение задачи можно посмотреть и проанализировать на отдельном листе.

Решение задач оптимизации в приложении Mathcad. В приложении Mathcad имеются встроенные функции, с помощью которых можно решать задачи оптимизации. Рассмотрим пример.

Пусть требуется определить оптимальные значения x1 и x2, которые обеспечивали бы максимум целевой функции

y = 1,7 + 4,56x1 – 3x2 – 0,69x1x2 – 0,44x2²

и удовлетворяли ограничениям:

3 <= x1<= 4, 0,1 <= x2 <= 0,9.

В рабочей области приложения Mathcad требуется записать:

f(x1, x2):= 1.7 + 4.56∙x1 – 3∙x2 – 0.69∙x1∙x2 – 0.44∙x2²

x1:= 3 x2:=0.1

Given

4 ≥ x1 ≥ 3

0.9 ≥ x2 ≥ 0.1

R:= maximize(f, x1, x2)

R =

Встроенная функция minimize позволяет решить задачи оптимизации, в которых нужно определить минимум целевой функции.

Назад

Приближенное решение дифференциальных уравнений

Рассмотрим дифференциальное уравнение первого порядка:

Требуется найти решение на интервале [x₀, x_n], удовлетворяющее начальному условию y(x₀) = y₀.

Для приближенного решения дифференциального уравнения интервал [x₀, x_n] разбивается на n частей с шагом h:

x_i+1 = x_i + h, i = 0, 1, 2, …, n – 1.

Согласно методу Эйлера значения y_i определяются по формуле

y_i+1 = y_i + h f(x_i, y_i).

Алгоритм метода Эйлера.

1. Ввод n, конечного значения x_n, начального значения x₀ (в переменную x), ввод y₀ (в переменную y).

2. Вычисление h =x = x₀, y = y₀.

3. Вывод x, y.

4. Вычисление y = y + hf(x,y), x = x + h.

5. Если x > x_n, то переход к пункту 6, иначе – переход к пункту 3.

6. Конец вычислений.

Например, пусть нужно найти решение дифференциального уравнения на отрезке [0, 1].

Зная начальные условия, определим y(0,01) и y(0,02):

y(0,01) = 1 + 0,01( – 21 + 0) = – 0,98;

y(0,02) = – 0,98 + 0,01( – 2( – 0,98) + 0,01) = –0,78.

Аналогичным образом определяются остальные значения y на отрезке [0, 1].

Для получения достоверных результатов значение h должно быть достаточно мало, при этом можно не выводить все получающиеся значения x и y. Целесообразно внести изменения в алгоритм программы так, чтобы вычисления проводились с малым шагом, а вывод результатов − с большим.

Расчетные формулы метода Рунге – Кутта четвертого порядка имеют вид:

k1 = hf(x_i, y_i),

k2 = hf(x_i + , y_i + ),

k3 = hf(x_i + , y_i + ),

k4 = hf(x_i + h, y_i + k3),

y_i+1 = y_i + (k1 + 2 k2 + 2 k3 + k4), x_i+1 = x_i + h, i = 0, 1, 2, …, n – 1.

Для разработки программы, реализующей метод Рунге – Кутта можно использовать тот же алгоритм, что и для метода Эйлера, внеся в него соответствующие изменения.

Решение дифференциальных уравнений в приложении Excel. Пусть имеется дифференциальное уравнение

x₀ = 0, y₀ = 1, h = 0,1.

Надо найти решение на отрезке [0; 1].

Программа решения этого уравнения методом Эйлера может иметь следующий вид:

Sub CommandButton1_Click()

х = Val(InputBox(“Введите начальное значение х”))

y = Val(InputBox(“Введите начальное значение y”))

хn = Val(InputBox(“Введите конечное значение х”))

h = Val(InputBox(“Введите шаг”))

i = 1

Do

y = y + h * (0.2 * y + x)

x = x + h

Cells(i, 1) = x : Cells(i, 2) = y : i = i + 1

Loop While x<= xn

End Sub

Решение дифференциальных уравнений в приложении Mathcad. В приложении Mathcad решить дифференциальное уравнение можно, записав формулы выбранного метода. Например, для решения методом Эйлера уравнения

x₀ = 0, y₀ = 1, h = 0,1

на рабочем поле приложения Mathcad надо записать:

h := 0.1 n := 3 i := 0..n x₀ := 0 y₀ := 1

x_i+1 = x_i + h y_i+1 = y_i + h (0.2∙y_i + x_i)

x= y =

И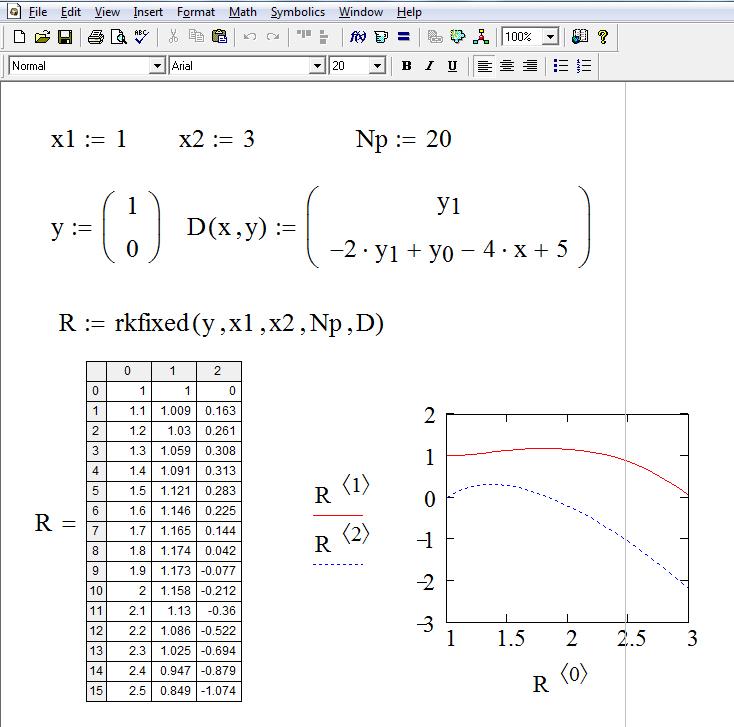меются также встроенные функции для решения дифференциальных уравнений, например функцияrkfixed.

На рисунке приведена страница документа в приложении Mathcad с решением системы дифферен-циальных уравнений

_{на отрезке [1; 3].}

Здесь x1, x2 – левая и правая границы интервала, на котором ищется решение; Np – число точек, в которых определяется решение; y₀, y₁ – начальные условия; D(x, y) – вектор правых частей системы.

На рисунке приведены также графики решения, характеризующие зависимость R(1, i) от R(0, i) и зависимость R(2, i) от R(0, i), т. е. зависимость y от x и зависимость z от x.

Назад

Приложение macromedia flash

Анимация формы. Для анимации формы нужно проделать следующие действия:

1. Создать исходный объект в первом кадре.

2. Выделить первый кадр на Timeline и на панели свойств Properties в поле Tween выбрать Shape. При этом в окошке Ease можно ввести число, которое задает скорость изменения промежуточных кадров.

3. Вставить пустой ключевой кадр (нажав <F7>) через нужное количество кадров от первого ключевого кадра. Создать новый объект, в который должен преобразоваться исходный.

4. Посмотреть результат, нажав клавиши <Ctrl> + <Enter> или выполнив команду Control / Play.

Для создания анимации с несколькими преобразованиями пункт 3 следует повторить нужное количество раз.

Чтобы применить анимацию формы к группам объектов или растровым изображениям, надо сначала разбить объекты на составляющие командой Modify / Break Apart. К тексту эту команду надо применить дважды, чтобы текст разбился на буквы, а они, в свою очередь, на составляющие.

Анимация движения. Можно анимировать расположение объекта, его размер, угол поворота, цвет, прозрачность. Для создания такой анимации следует:

1. Создать исходный объект. Выделить его инструментом Arrow Tool и выполнить команду Modify / Group.

2. Выделить первый кадр на Timeline и в инспекторе свойств Properties в поле Tween выбрать Motion (или выполнить команду Insert / Create Motion Tween).

3. Вставить следующий ключевой кадр через некоторое количество кадров от первого (нажав <F6>). При этом временная шкала Timeline должна окраситься в сиреневый цвет. Переместить объект в нужное место (пункт 3 повторяется нужное число раз.)

4. Посмотреть результат, нажав клавиши <Ctrl> + <Enter> или выполнить Control / Play.

На панели свойств можно отрегулировать скорость кадров (пункт Frame rate). Такая анимация предполагает движение фигуры из начального положения в конечное по кратчайшей траектории.

Анимация движения по заданной траектории. В приложении Macromedia Flash существует понятие ведущего слоя Guide Layer. На него можно поместить какие-либо комментарии, которые видны только в режиме редактирования фильма, и с его помощью можно также управлять траекторией перемещения объекта. Для создания анимации движения по заданной траектории надо: