Файл: Informatika2013-Of2010.doc

Дифференцирование и интегрирование. Для выполнения операций дифференцирования или интегрирования надо ввести выражение, стоящее под знаком дифференциала, или подынтегральное выражение, выделить переменную дифференцирования или интегрирования и выполнить Символика / Переменная / Дифференциация или Интеграция (Symbolics / Variable / Differentiate или Integrate).

Можно ввести нужное выражение производной или интеграла с помощью панели Матанализ (Calculus) и записать оператор символьного вывода →. Например:

Матричные вычисления. Для создания матрицы надо ввести ее имя, знак присваивания и выполнить Вставка / Матрица (Insert / Matrix) либо нажать кнопку Матрица или вектор (Matrix or Vector) на панели Матрица (Matrix) либо «горячие» клавиши <Ctrl> + <M>.

В появившемся окне задать количество строк и столбцов, затем ввести конкретные значения элементов матрицы. Ниже приведена запись матрицы А2 размерности 33.

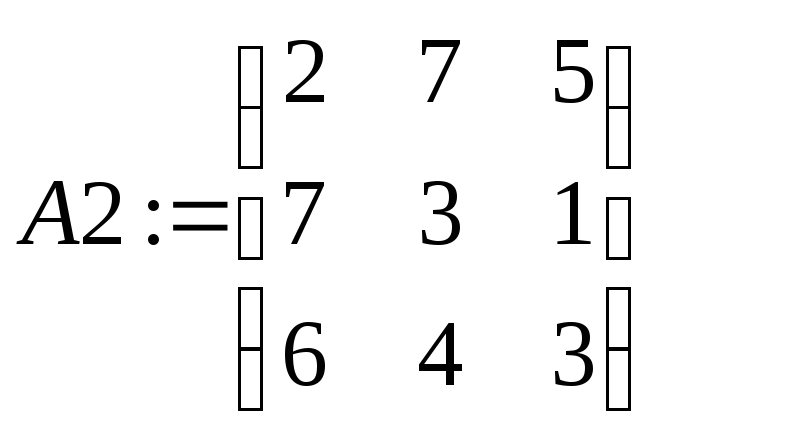
Нумерация элементов массива начинается с нуля. Mathcad допускает обращение к отдельным элементам матриц и векторов с помощью нижних индексов и к столбцам матриц с помощью верхних индексов.

Нижние индексы вводятся с помощью кнопки Хn на панели Матрица или клавишей открывающей квадратной скобки ([). Нижние индексы, если их несколько, отделяются друг от друга запятой.

Верхние индексы вводятся кнопкой М^<> на панели Матрица или комбинацией клавиш <Ctrl> + <6>.

П

Затем поместить курсор в то место, куда требуется вставить график, и при помощи Вставка / График (Insert / Graph) или панели График (Graph) выбрать X-Y график (X-Y Plot) или Полярный график (Polar Plot). Можно использовать также клавишу @.

В появившейся пустой области графика в местозаполнители возле осей надо ввести имена аргумента и функции (для нескольких – через запятую).

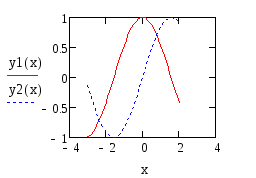
На рисунке представлены два графика для значений х, меняющихся от –3 до 2 с шагом 0,1:

x: =  –3,–2.9..2

y1(x):= cos(x)

y2(x):= sin(x)

Назад

Вычисление определенных интегралов

Приближенное вычисление определенного интеграла основано на геометрическом смысле интеграла и сводится к приближенному вычислению площади, ограниченной графиком подынтегральной функции f(x), прямыми x = a = x₀, x = b = x_n и осью OX. Интервал [a, b] делится на n равных частей длиной . Тогда значениямx_i = x _{i  1} + h, i = 1, 2, ..., n соответствуют значения y_i = f(x_i).

Согласно методу левых прямоугольников, искомая площадь вычисляется как сумма площадей прямоугольников, основание которых равно h, а высота равна соответственно y₀ для первого прямоугольника, y₁ – для второго и т. д. вплоть до последнего с высотой y _{n  1}. Тогда

Приближенное значение определенного интеграла по методу правых прямоугольников вычисляется по формуле

Согласно методу трапеций значение интеграла определяется по формуле

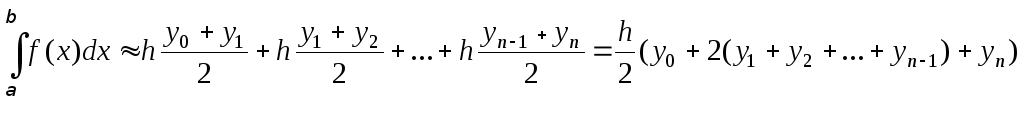
Например, для n = 5 метод трапеций дает следующее выражение для приближенного вычисления интеграла:

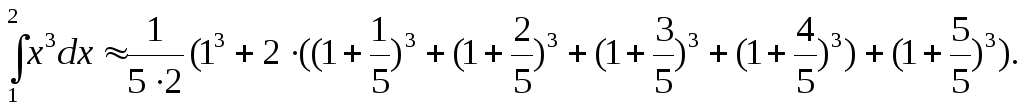
Здесь h = (2 – 1) / 5, y₀ = 1³, y₁ = (1+1 / 5)³ и т. д.

Рассмотрим алгоритм метода трапеций.

1. Ввод a, b, n.

2. Вычисление , x = a + h, s = 0.

3. Расчет s = s + f(x), x = x + h.

4. Если x > (b – h), то переход к пункту 5, иначе – переход к пункту 3.

5. Вычисление значения интеграла

6. Вывод z.

При использовании метода парабол для вычисления определенного интеграла интервал [a, b] делится на четное количество частей – 2n. Тогда , x_i = x_i–1 + h, i = 1, 2, …, 2n.

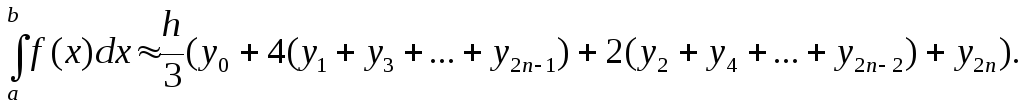
Алгоритм метода парабол

1. Ввод a, b, n.

2. Вычисление 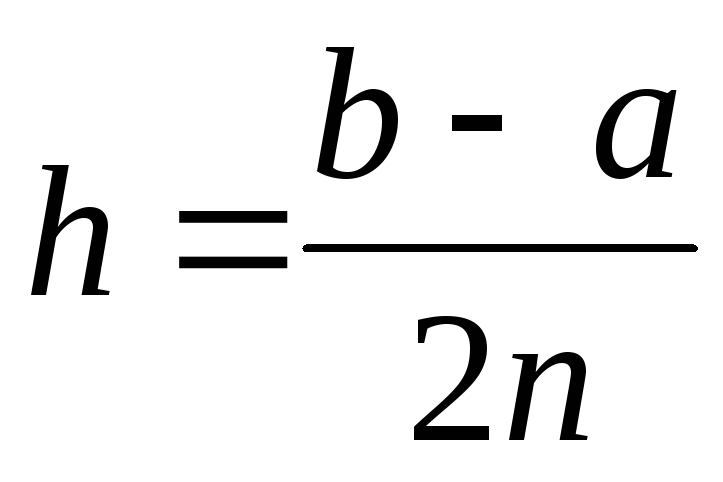, x = a + 2h, s1= 0, s2 = 0, i = 1.

3. Расчет s2 = s2 + f(x) , x = x + h, s1 = s1 + f(x), x = x + h, i = i + 1.

4. Если i < n – 1, то переход к пункту 3, иначе – переход к следующему пункту.

5. Вычисление значения интеграла:

6.  

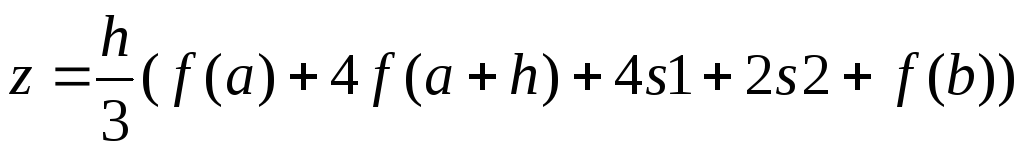
7. Вывод z.

Здесь s1 = y₃ + y₅ + … + y_{2n  1}, а s2 = y₂ + y₄ + … + y_{2n  2}.

Приближенное вычисление интеграла в приложении Excel. В приложении Excel можно составить программы по алгоритмам, приведенным выше, на языке VBA. Рассмотрим пример.

Пусть на рабочем листе Excel в ячейках А1, А2, А3 располагаются значения a, b и n. На этом же листе можно создать кнопку и составить для неё программу вычисления, например, интеграла методом левых прямоугольников.

Sub CommandButton_Click()

a = Range(“A1”)

b = Range(“A2”)

n = Range(“A3”)

h = (b  a) / n : S = 0

For x = a To b  h Step h

S = S + Fint(x)

Next

z = h * S

Range(“A4”) = z

End Sub

Подпрограмма записывается на листе кода до или после основной программы.

Function Fint(x)

Fint = x ^ 3

End Function

Здесь a = 1, b = 2, значение n можно определить достаточно большим, например, n = 200. Функция пользователя Fint(x) вычисляет значение подынтегральной функции.

Для вычисления интеграла методом правых прямоугольников надо в вышеприведенной программе внести изменения в оператор For: For x = a + h To b Step h

Приближенное вычисление интеграла в приложении Mathcad. Для вычисления определенного интеграла в приложении Mathcad нужно записать интеграл, подынтегральную функцию и пределы интегрирования. Например:

Для получения численного значения записывается выражение:

z =

Назад